集训记录

\(\text{Lecture 2}\).

1. Painter’s Studio (POI1998)

• 首先找规律。发现这个分形是每次平分，考虑二进制。
• 容易发现 \(a_{i, j} = 1\) 的条件是不存在任意 \(i\) 使得 \(a_i < b_i\)。
• 考虑平移之后。\((i, j) \rightarrow (i + x, j + y)\) 都要是 \(1\)。问题转化。
• \(f_{i, p, q}\) 表示从低往高第 \(i\) 位，\(p\) 是 \(a + x\) 的进位，\(q\) 是 \(b + y\) 的进位。

2. bit compressor

• 确定顺序：从右往左。（存疑）
• 考虑元素：压缩前 \(t_0\) 个 \(0\)，压缩前 \(t_1\) 个 \(1\)。其中 \(t_0 \leq 40\) 比较特殊。
• 转移显而易见。

\(fail_v = [s_v == s_{ch_{fail_u}}]ch_{fail_u}\)

3. Walk Through Squares

• 首先考虑字符串匹配经典做法：字典树，AC 自动机，KMP。
• 把模式串建到 Trie 上，使用 AC 自动机。
• \(f_{i, j, p \in \{0, 1\}, q \in \{0, 1\}, t}\) 表示当前在 \((i, j)\)，是否出现 \(s_1 \or s_2\)，在 Trie 上的节点编号是 \(t\)。
• 转移同 AC 自动机，显然。

\(\text{Lecture 3.}\)

1. Fun Game

• 假设答案长度是 \(m\)。
• 如果 \(\exists \ i, m \leq | \ s_i \ |\)，则我们可以暴力处理这一部分。
• 接下来便只有 \(\forall i, m > | \ s_i \ |\)。
• 然后有一个显然的性质：若 \(s_i\) 是 \(s_j\) 的字串，则 \(s_i\) 为冗余的字符串，可以删除。
• 注意到 \(n \leq 16\)，考虑状压 \(dp\)。
• 设 \(f_{i, mask, k\in\{0, 1\}}\) 表示当前最后一个串为 \(s_i\)，目前选择了 \(mask\) 状态的字符串，\(k\) 表示 \(s_i\) 是正向还是反向。转移显然，\(dp\) 的时间复杂度应该是 \(\mathcal{O}(2 ^ n \times n ^ 2)\)。
• 状态定义有一个细节：如果新加入的字符串 \(t\) 与不止两个字符串相关（即可能要用到选择字符串的倒数第二个），则倒数第一个字符串 \(s\) 一定是 \(t\) 的字串，矛盾。
• 当然，字符串是可以首尾相接的。由于整个图是环，所以我们可以再在 \(dp\) 状态里增加细节，强行定义 \(dp\) 以 \(s_1\) 开始。这样我们就可以直接计算开头和结尾的最大 \(\text{border}\)。
• 时间复杂度顶峰是 \(dp\)。

2. The Best Name for Your Baby

3. ADVEDIST - Advanced Edit Distance

• 首先如果去掉交换操作，就是普通的编辑距离，可以 \(dp\) 解决。
• 但是加上交换操作后容易发现不能按照如上方式 \(dp\)，得另辟蹊径。
• 考虑挖掘交换性质。发现交换一定是选择近端。因此只需考虑一种交换方案。
• 假设我们枚举了 \(k_1, k_2\)，则需要先删除 \(i - k_1 + 1\) 再插入 \(j - k_2 + 1\)。
• 于是可以在编辑距离的基础上再增加转移方程。

4. Beautiful Bridges

• 首先可以写出 naive 的暴力 \(f_i = \min\{dp_j + cost_{i, j}\}\)。

• 如果我们要判断是否合法，则一定有一个点在拱内。可以看圆心，复杂度 \(\mathcal{O}(n^3)\)。

• 我们考虑一边移动 \(j\) 一边判断合法性，解一元二次方程 \((x - a) ^ 2 + (y - b) ^ 2 \leq r ^ 2\)。（？）

• 时间复杂度可以优化到 \(\mathcal{O}(n ^ 2)\)。

5. 最优切割

• 首先显然可以使用区间 \(dp\)。
• 但是在选择决策点的时候是可以贪心的。
• 我们先枚举断掉一条边，然后对于任意两个相邻的剩余部分选择较小的一条。
• 一定是存在一种方案使得可以满足的。（证明显然）

6. 小 Y 的背包计数问题

• 很妙的。由于 \(n \leq 10^5\)，而且物品数量还是严格递增的，容易想到根号分治。
• 当 \(m \leq \sqrt{n}\) 时，可以使用朴素 \(dp_{i, j}\)。时间复杂度 \(\mathcal{O}(n\sqrt{n})\)。
• 当 \(m > \sqrt{n}\) 时，容易发现物品数量的限制是没有用的。因此可以看作无线取数。
• 显然朴素 \(dp\) 状态爆炸，则我们可以考虑 \(g_{i, j}\) 表示划分了 \(i\) 个数的差分数组（不严格递增）且和为 \(j\) 的方案数。
• 此时有一种很妙的转移方法。我们可以在后面放一个新数，或者整体加 \(1\)。

\(\text{Lecture 4.}\)

1. Maximum path

• 题目不好做，进行观察。注意到 \(n = 3\)，考虑发掘性质。
• 容易发现，当你在第一行或者第三行往左走，是会走到封闭区间里的。因此，向左走只能是第二行。
• 第二行向左走是蛇形走位的形态，所以我们可以考虑设计 \(dp\)，因为目前的模型已经简化了很多（可以不用考虑更多的路径重复问题）
• 根据直觉与内心的意志，我们猜想向左走不会特别多。事实也证明了这一点，一次连续的向左移动可以被不向左移动平替。因此，只有单位蛇形走位是可行的，其他都可平替。具体可以通过如下方案替换。

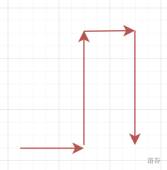
• 因此，我们可以只考虑单位 S 形。转移比较简单。

2. Exclusive Access 2

• 发现虽然答案形式很二分，但是容易发现二分其实比较困难。于是思考性质。
• 题目说需要确定此图为 DAG，因此性质可能比较多。考虑观察。
• 如果我们按照最长路 \(d_i\) 来对 \(dp\) 进行分层，有一个美好的性质：同层的点不会进行连边。
• 于是我们可以尝试状压 \(dp\)。转移还是比较简单的。
• 枚举一个数的子集有一种技巧：for (int s = mask; s; s = mask & (s - 1))。感觉还是很聪明的。

3. Routing

• 神仙题。特殊的定义。

• 设 \(f_{i, j}\) 表示从 \(i \rightarrow 1 \rightarrow j\) 经过最少的点集合大小。通过这种奇妙定义可以使得 \(f_{2, 2}\) 为答案。

• 然后没怎么看懂（？），有点困难。

4. Little Bishops

• 旋转 \(45\degree\)，状压秒了。

5. Queue

• 见到这种高度的题比较典型的 trick 是考虑极端值。
• 如果考虑最高的就是区间 \(dp\) 了，但是我们可以考虑最低的高度。
• 这样子我们会发现最低的高度除了能跟相邻的对互相看见，对整体没有任何影响。
• 因此直接 \(dp\) 即可，注意需要考虑在两侧和在中间的情况。