浅谈一类网络流问题以及相关定理

前言 & 框架

本文是笔者的一个长期目标，预期在该学期结束前完工，目前还在构思阶段。

以下是文章的大致框架：

• √ 网络流入门
  • √ 网络流相关概念
  • √ FF 算法 & EK 算法
  • √ 最小割最大流定理
• √ 割
  • √ Menger's 定理
  • √ 最小割的唯一性
• 网络流相关应用
  • √ 最大权闭合子图
  • √ 最大密度子图
  • 最小权点覆盖 & 最大权独立集
• 网络流再探
  • 上下界可行流问题（无源无汇 & 有源有汇）
  • Dinic 算法
    • 当前弧优化
• 回顾二分图
  • 二分图的三类边
  • 残量网络的强连通分量与最大匹配 M 的选择无关
  • Dulmage Mendelsohn 分解
• 网络流习题略讲

---

网络流入门

网络流相关概念

一个网络是一张有向图 \((V, E)\)，其中每条边都有一个容量 \(c(u,v)\)。一个网络有一个源点 \(S\) 和一个汇点 \(T\)。

网络流满足以下几条性质：

• 流函数 \(f : (x, y) \rightarrow \text{R}\) 是一个二维数对到实数域上的一个映射。

• 容量限制：\(f(x, y) \leq c(x, y)\)。

• 斜对称：\(f(x, y) = -f(y, x)\)。

• 流量守恒：\(\forall i \neq S, i \neq T, \sum f(u, i) = \sum f(i, v)\)。

以下是网络流的相关定义。

• 对于有源汇网格，\(\sum f(S, v) = \sum f(u, T)\)，也就是初始流量和结束流量相等。

• 残量网络 \(G_f = (V, E_f)\)：\(c(u, v)_f = c(u, v) - f(u, v)\)，若 \(c(u, v)_f = 0\)，则视为 \((u, v) \not \in E_f\)。

• 增广路：残量网络 \(G_f\) 上的一条从 \(S\) 到 \(T\) 的一条路径。

• 割：将点集划分成 \(A, B\)，则称这个划分为一个割。这个割的流量为 \(\sum_{u \in A, v \in B} f(u,v)\)。这个割的容量为 \(\sum_{u \in A, v \in B} c(u,v)\)。若 \(u \in A, v \in B\)，则称 \((A, B)\) 为割边。

• 净流量：\(f(u) = \sum\limits_{x \in V} f(u, x)\)。这里有一个定理，除了 \(S\) 和 \(T\) 外，都有 \(f(i) = 0\)。

其中，增广路和割是网络流中核心的，反复出现的两个概念。

我们定义一个流的流量是 \(f(S) = \sum\limits_{x \in V} f(S, x)\)。同时，这个值也是 \(-f(T)\)。

FF 算法 & EK 算法

先来明确问题。

最大流问题

给定一个网络 $(V, E)$，你需要求出这个网络的最大流量。

这个最大流量就是最大流。

接下来，我们来给出两种解法，分别被称为 Ford–Fulkerson（FF）增广和 Edmonds–Karp（EK）算法。

Ford-Fulkerson 增广

我们考虑在残量网络上找到一条增广路。假设这条增广路上 \(c(u,v)_f\) 的最小值为 \(w\)，那么我们给这条增广路上的那些边在原网络上的流量全部增加 \(w\)。（对应的，在残量网络上，这些边会减少 \(w\)）

容易发现，这样操作后，\(S\) 的净流量会增加 \(w\)。于是我们不断地去增广，直到没有增广路了就停下来。这时候的流量就是该网络的最大流量。

显然，由于每次流量都会增加 \(w > 0\)，所以这个增广次数是有限的。

以上就是 FF 算法的大致流程。接下来我们来解释几个问题。

Q1：如何理解「负流量」，这个东西有什么意义吗？

A1

实际上，「负流量」代表的是一个「反悔」的思想。

我们注意一条边 \((u, v)\) 在残量网络上的表现，会有 \(c(u, v)_f = c(u, v) - f(u, v)\)，且 \(c(v, u)_f = 0 - f(v, u) = f(u, v)\)。

考虑如果正向边 \((u, v)\) 被增广了，那么这比较好理解，就是一些新的流经过了 \((u, v)\) 这条边。

如果是反向边 \((v, u)\) 被增广了，那实际上相当于我们「反悔」了原来一些经过 \((u, v)\) 的流量，来纠正之前增广路选择顺序的错误。

举个例子，在下图中，如果我们先选择了 \(u \to v\) 这条增广路，但实际上最优选择是 \(u \to q, p \to v\)。那么，在后续的增广中，我们能选择 \(p \to v \to u \to q\)，这样我们反悔了 \(u \to v\) 这条边，并使总流量增加了。

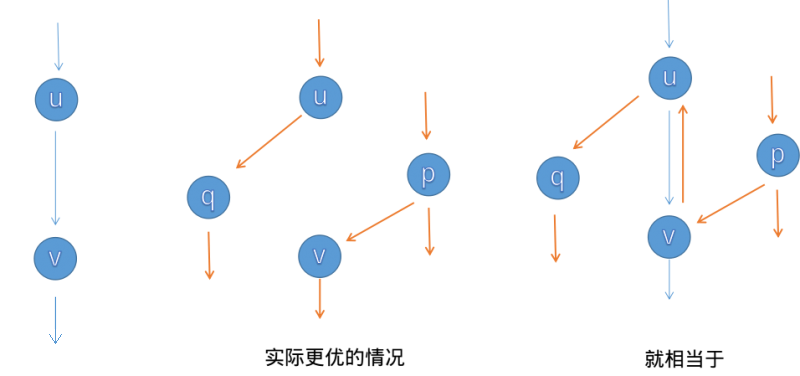
以上案例告诉我们，退流操作带来的「抵消」效果使得我们无需担心我们按照「错误」的顺序选择了增广路。

Q2：为什么这样不断增广，最后增广不出来时，流量一定是最大流？

A2

这个问题其实与最小割最大流问题等价，所以我们马上会提到。

最小割最大流定理（MCMF 定理）

对于一个网络，它的最小的割的容量就是最小割。

MCMF 定理

给定一个网络 $(V, E)$，这个网络的最大流等于最小割。

可以将上面的问题拆成两部分来证明。

• 任意一个流的流量都小于等于任意一组割的容量。

对于任意一个流和任意一组割，考虑观察一单位流量的贡献。

假设这一组割的点集为 \(A, B\)，设这一单位流量从 \(A\) 向 \(B\) 的次数是 \(t\)，从 \(B\) 向 \(A\) 的次数是 \(f\)，显然会有 \(t = f + 1\)。

那这一单位流量对割的流量会造成正向的 \(t\) 贡献和 反向的 \(-f\) 贡献，也就是 \(t - f = 1\)。

因此，割的流量等于流的流量。又有割的流量小于等于容量，因此任意一个流的流量都小于等于任意一组割的容量。

• 存在一个流和一组割，使得该流的流量等于该割的容量

考虑刚才 FF 算法不停增广直到没有增广路后，得到的那一组流。

考虑该流的残量网络，由于不存在增广路，因此残量网络不连通。

我们取 \(A\) 为 \(S\) 在残量网络中能到达的所有点，\(B\) 为不在 \(A\) 中的点，这样就能构造出来一个割。

由于这个割有容量的那些边在残量网络上都没有，所以这些边肯定被流满了，则这个割的容量等于割的流量。

根据上面我们得到的结论，可以证明该割的流量等于流的流量。因此，流的流量等于割的容量。

A2

我们现在再来解答上面 Q2 的问题。显然，我们可以对 FF 算法得到的流构造出一组割，使得该流的流量等于割的容量。

然后，由于所有的流，流量都小于等于最小割，而这个流等于这个割，则这个流的流量一定是最大流。

Edmonds-Karp 算法

算法流程

前文中，我并没有分析 FF 算法的复杂度。但其实显然，这个算法的复杂度是非多项式的，和总流量的大小有关，太慢了。

因此，我们可以尝试优化 FF 算法。

我们关注选择增广路这一个步骤。FF 算法中，我们默认是随便选择一个增广路。

如果我们每次选择的增广路是最短的增广路的话，就会发生变化，可以证明时间复杂度是 \(\mathcal{O}(nm^2)\) 的，而这个算法就被称作 Edmonds-Karp 算法。

我们简单概括一下 EK 算法的流程。

• 我们从 \(S\) 开始，在残量网络上 BFS，寻找到达 \(T\) 的最短增广路。如果到达不了 \(T\)，就说明没有最短路了，算法结束。
• 否则，我们需要还原一下那条最短路径，因此需要在 BFS 的过程中记录 \(u\) 的最短路是从哪个点来的。
• 对于这条增广路 \(p\)，我们计算一下这条增广路在残量网络上的边权最小值 \(w\)。然后，对于增广路上的一条边 \(u \to v\) 来说，我们要令 \(f(u, v)\) 增加 \(w\)，\(f(v, u)\) 减少 \(w\)，\(c(u, v)_f\) 减少 \(w\)，\(c(v, u)_f\) 增加 \(w\)，同时当前流的流量会增加 \(w\)。
• 增广完毕后，我们会得到一个新的残量网络 \(G_f\)，重新对 \(G_f\) 进行 BFS 寻找增广路即可。

时间复杂度分析

EK 算法的时间复杂度证明比较困难，而且没什么可扩展性，读者可以选择不看这一部分，只用知道 EK 的时间复杂度是 \(\mathcal{O}(nm^2)\) 的即可。

感兴趣的同学可以阅读。

EK 算法复杂度证明

我们先引入一个引理：最短路非递减引理。

最短路非递减引理

我们定义 $d_f(u)$ 表示在残量网络 $G_f$ 中，$S$ 到 $u$ 要经过的最小边数。那么，设 $f'$ 是 $f$ 经过一次增广得到的流，且在 $f, f'$ 的残量网络中，$S$ 都能到达 $u$，则有 $d_f(u) \leq d_{f'}(u)$。

---

反证。假设当前有若干个点，它们的 $d_{f'}(x) < d_{f}(x)$，那我们取这其中 $d_{f'}(x)$ 最小的那一个点 $v$。

根据反证的假设，\(d_{f'}(v) < d_{f}(v)\) 为已知条件。

考虑点 \(u\)，使得 \(d_{f'}(u) + 1 = d_{f'}(v)\)。也就是说，\(u\) 是在残量网络 \(G_{f'}\) 上在 \(S \to v\) 的最短路中 \(v\) 之前的那一个点。

由于 \(v\) 要是所有满足 \(d_{f'}(x) < d_{f}(x)\) 中最短路最小的点，因此 \(u\) 只能满足 \(d_{f'}(u) \geq d_f(u)\)。

根据 \(d_{f'}(u) \geq d_f(u)\) 和 \(d_{f'}(u) + 1 = d_{f'}(v)\)，我们有 \(d_{f'}(v) - 1 \geq d_{f'}(u)\)。又 \(d_{f}(v) > d_{f'}(v)\)，因此 \(d_{f}(v) - 1 > d_{f'}(u)\)。

整理一下，我们能得到 \(d_{f}(v) > d_{f'}(u) + 1\)。这是一个很强的结论，根据这个结论，我们考虑 \((u, v)\) 是否在 \(G_f\) 中。

• 如果 \((u, v)\) 在 \(G_f\) 中，那么 \(d_{f}(u) + 1 \geq d_f(v)\)。又 \(d_{f'}(u) \geq d_f(u)\)，因此 \(d_{f'}(u) + 1 \geq f_u\)，矛盾。

• 如果 \((u, v)\) 不在 \(G_f\) 中，那么由于 \(d_{f'}(u) + 1 = d_{f'}(v)\)，则 \((u, v)\) 在 \(G_{f'}\) 中。这说明，\((v, u)\) 在 \(f\) 向 \(f'\) 的增广中被增广了，然后使 \(f(u, v)\) 减少，从而 \(c(u, v)_f\) 增大。\((v, u)\) 要被增广，需要 \(d_{f}(v) + 1 = d_{f}(u)\)。又 \(d_{f'}(u) \geq d_f(u)\)，因此 \(d_{f'}(u) - 1 \geq f_u\)，矛盾。

证毕。

有了这个引理，我们就能证明 EK 的增广轮数是 \(nm\) 量级的了。

我们称一条增广路上，\(c(u, v)_f\) 最小的那条边是饱和边。我们随便取出来这次增广操作上的一条饱和边 \((u, v)\)。

由于 \((u, v)\) 的 \(c(u, v)_f\) 最小，那么这条增广路的流量就是 \(w = c(u, v)_f\)。所以，\((u, v)\) 会在增广之后从残量网络 \(G_f\) 中消失，然后 \((v, u)\) 会出现并达到最大值。

根据上述信息，我们可以整理出 \(d_f(u) + 1 = d_f(v)\)。假设 \(f'\) 为 \((v, u)\) 即将被增广前的流，就有 \(d_{f'}(v) + 1 = d_{f'}(u)\)。根据最短路非递减引理，有 \(d_f(v) \leq d_{f'}(v)\)。

因此，\(d_{f'}(u) \geq d_{f'}(v) + 1 \geq d_f(v) + 1 = d_f(u) + 2\)，得到 \(d_{f'}(u) \geq d_f(u) + 2\)。

所以，饱和边 \((u, v)\) 的增广到 \((v, u)\) 被增广，会使得 \(d(u)\) 至少增加 \(2\)。又由于 \(d(u)\) 至多是 \(n\)，因此每条边被选为饱和边的次数至多是 \(n\) 次。

每次增广至少会带一条饱和边，而饱和边的总数至多是 \(nm\)，因此增广次数至多是 \(nm\)。证毕。

代码实现

Edmonds-Karp 算法模板

namespace Edmonds_Karp {
    int vis[K], pre[K];
    long long dis[K], ans;
    bool findPath(int x, int t) {
        queue <int> q;
        fill(vis + 1, vis + n + 1, 0);
        fill(dis + 1, dis + n + 1, 0);
        q.push(x); vis[x] = 1; dis[x] = 2e18;
        while (!q.empty()) {
            int u = q.front(); q.pop();
            if (u == t) return true;
            for (int i = hd[u]; i > 1; i = e[i].nxt) {
                int v = e[i].v;
                if (e[i].w == 0) continue;
                if (vis[v]) continue;
                dis[v] = min(dis[u], e[i].w);
                pre[v] = i;
                q.push(v);
                vis[v] = 1;
            }
        }
        return false;
    }
    void update(int s, int t) {
        int x = t;
        while (x != s) {
            int v = pre[x];
            e[v].w -= dis[t];
            e[v ^ 1].w += dis[t];
            x = e[v].u;
        }
        ans += dis[t];
    }
    long long Edmonds_Karp(int s, int t) {
        ans = 0;
        while (findPath(s, t))
            update(s, t);
        return ans;
    }
}

割

门格尔（Menger）定理

Menger 定理其实本来不应该出现在网络流这里，因为它属于图论。但是，由于这个定理是 MCMF 定理的推论，所以简单提一下，不作证明。

该定理有以下的两种形式：

• 点形式：对于 \(u, v\)，其中 \(u \neq v\)，使 \(u, v\) 不连通所需要删除的最小点数等于 \(u\) 到 \(v\) 的最多的不相交路径数。
• 边形式：对于 \(u, v\)，其中 \(u \neq v\)，使 \(u, v\) 不连通所需要删除的最小边数等于 \(u\) 到 \(v\) 的最多的边不相交（点可以）路径数。

最小割的唯一性

考虑如下问题。

BZOJ-1797 / 最小割的唯一性

给定一个网络 $(V, E)$，对于每条边，你需要回答两个问题：

• 这条边是否可能在最小割中。
• 这条边是否必须在最小割中。

最小割的充要条件

考虑一个割 \(A, B\) 要是最小割的充要条件。我们先随便跑出来一个残量网络。

我们在 MFMC 定理的证明中提到了，流的流量等于割的流量。如果我们要割的容量最小，我们就需要这些从 \(A\) 到 \(B\) 的边满流，这样割的流量才会等于割的容量。

因此，在残量网络上，上面结论的表现就是不存在一条从 \(A\) 到 \(B\) 的边。

现在回到原问题。

边可能在最小割中的充要条件

这就相当于，我们要把 \(u\) 和 \(v\) 分别分到 \(A, B\) 集合里，使得残量网络上不存在 \(A\) 向 \(B\) 的边。

首先，\(u \to v\) 这条边肯定要满流，不然残量网络上会存在 \(u \to v\) 这条边，导致这个割不满足最小割的充要条件。

然后，我们会发现，\(u\) 的后继都要在 \(A\) 集合里，\(v\) 的前驱都要在 \(B\) 集合里。如果 \(u\) 是 \(v\) 的前驱，\(v\) 是 \(u\) 的后继，就会导致矛盾。因此，\(u, v\) 也不能在同一个 SCC 内。

所以结论就是\(u \to v\) 满流且 \(u, v\) 不在同一 SCC 内。

边必须在最小割中的充要条件

首先，这个边肯定要满足上一个问题的条件，也就是 \(u \to v\) 满流且 \(u, v\) 不在同一 SCC 内。不妨先将残量网络缩点。

我们考虑 \(A, B\) 这两个集合必须要有哪些点。和上面的问题类似，\(S\) 的后继都要在 \(A\) 中，\(T\) 的前驱都要在 \(B\) 中。

我们可以说明，如果 \(u\) 是 \(A\) 的必要点，\(V\) 是 \(B\) 的必要点，那么 \((u, v)\) 这条边就一定会出现在最小割中。

所以结论就是\(u \to v\) 满流且 \(u\) 是 \(S\) 的后继，\(v\) 是 \(T\) 的前驱。

实际上，上面的问题还存在等价结论\(u \to v\) 满流且 \(u\) 与 \(S\) 同强连通块，\(v\) 与 \(T\) 同强连通块。这个结论自证不难，简单说就是根据上面的结论，再加上存在 \(u \to S\) 的路径和 \(v \to T\) 的路径。（要利用 \(u \to v\) 满流）

残量网络的强连通性

咕。

网络流经典模型

最大权闭合子图

问题描述

给定一个有向图，你需要选择一个点集 $S$，使得对于所有 $x \in S$，$x$ 的后继都在 $S$ 中。在此基础上，每个点有一个整数权值 $a_i$，你需要使得 $\sum\limits_{x\in S} a_x$ 最大。

我们可以给出一个构造，使得我们可以通过最小割解决这个问题。

我们新建一个源点和汇点 \(s, t\)，并将 \(a_i > 0\) 和 \(a_i \leq 0\) 的数划分开来。

我们从 \(s\) 向每一个 \(a_i > 0\) 的 \(i\) 连边，边权为 \(a_i\)，并从每一个 \(a_i \leq 0\) 的 \(i\) 连向 \(b_i\)，边权为 \(-a_i\)，则答案就是 \(\sum_{x}[a_x > 0]a_x\) 减去最小割。然后，对于原图上每一条 \((u, v)\) 的有向边，我们都在新图上建一条 \(u\) 向 \(v\)，边权为 \(+\infty\) 的边。

这很容易说明。我们令最小割为 \(A, B\)，则我们断言 \(A\) 点集中的点除了源点都属于 \(S\)。

• 如果一个正权点 \(x\) 不在 \(A\) 里，则 \(s \to x\) 的边要割掉，贡献为 \(a_x-a_x = 0\)。
• 如果一个正权点 \(x\) 在 \(A\) 里，则 \(s \to x\) 的边不用割，贡献为 \(a_x - 0 = a_x\)。
• 如果一个非正权点 \(x\) 不在 \(A\) 里，则 \(x \to t\) 的边不用割，贡献为 \(0\)。
• 如果一个非正权点 \(x\) 在 \(A\) 里，则 \(x \to t\) 的边要割掉，贡献为 \(-(-a_x) = a_x\)。

因此，这个答案完全等于 \(S = A - \{s\}\) 时的权值，并且最小割求出来的也恰好是最大权。

最大密度子图

问题描述

给定一个有向图，你需要选择一个子图 $(V, E)$，你需要使得 $\dfrac{|E|}{|V|}$ 最大。

首先显然是导出子图最优。

考虑二分密度 \(\lambda\)，问题转化为判定是否存在子图，其密度 \(\geq \lambda\)，也就是 \(0 \geq |V| \times \lambda - |E|\)。

---

考虑最小化这个值。我们观察一条边 \((u, v)\)，这条边存在当且仅当 \(u, v\) 都存在于 \(V\) 中。

因此，可以建出最大权闭合子图的模型：每个点点权为 \(-\lambda\)，每条边建一个点表示，点权为 \(1\)，边 \((u, v)\) 所代表的点连向 \(u, v\)。

---

当然，存在更加优秀的做法，但较为困难。

如下图，我们想要通过点集 \(V\) 计算 \(|E|\)，那么不妨容斥一下，我们考虑红色的边，这些边的个数是 \(V\) 与 \(V\) 的补集组成的割的容量。我们只要拿与 \(|V|\) 相关的边数减去割的容量就可以得到 \(|E|\)。

简单推一下式子（其中 \(V'\) 是 \(V\) 的补集）：

\[\begin{aligned} \lambda \times |V| - |E| & = \sum_{v \in V} \lambda - \sum_{v \in E} 1\\ & = \sum_{v \in V} \lambda - (\dfrac{\sum_{v \in V} d_v}{2} - c[V, V'])\\ & = \sum_{v \in V} (\lambda - \dfrac{d_v}{2}) + c[V, V'] \end{aligned} \]

根据这个建图跑最小割即可。

最小权点覆盖 & 最大权独立集

先咕了，感觉没啥用。

网络流再探

上下界可行流问题（无源无汇 & 有源有汇）

咕。

Dinic 算法

咕。

回顾二分图

二分图的三类边

咕。

Dulmage Mendelsohn 分解

咕。

网络流习题略讲

最大流

咕。

最小割

咕。

费用流

咕。

流与贪心

CF724E（\(\mathbf{Hard. 0.1}\)）

首先转化为最大流问题，建图是朴素的，我们 \(s \to i\) 连一条 \(p_i\) 的边，\(i \to t\) 连一条 \(s_i\) 的边。

由 MCMF 定理，我们将这道题转化为求最小割。那么考虑 DP，设 \(f_{i, j}\) 为前 \(i\) 个数，我们确定存在 \(j\) 条 \(s \to x\) 的边没有被割掉，转移是朴素的。一个小细节就是可以证明最优解不会存在 \(s \to x\) 且 \(x \to t\) 两条边都被删掉的情况，感兴趣的读者可以尝试证明。

设 \(a_i = (n - i)c + s_i - p_i\)，然后枚举最终有 \(x\) 个点存在 \(s \to x\) 的边。那我们按照 \(a\) 的大小排序，显然会选择前 \(x\) 小的数，然后加上一个和 \(x\) 有关的多项式即可。

点击查看代码

#include <bits/stdc++.h>
using namespace std;

const int N = 1e4 + 7;

long long read() {
    long long x = 0, k = 1; char c = getchar();
    while (c != '-' && (c < '0' || c > '9')) c = getchar();
    if (c == '-') k = -1, c = getchar();
    while (c >= '0' && c <= '9') x = (x << 1) + (x << 3) + (c ^ 48), c = getchar();
    return x * k;
}

int n;
long long c, p[N], s[N], a[N];

signed main() {
    n = read(), c = read();
    for (int i = 1; i <= n; i ++) p[i] = read();
    for (int i = 1; i <= n; i ++) s[i] = read();
    for (int i = 1; i <= n; i ++)
        a[i] = s[i] + c * (n - i) - p[i];
    sort(a + 1, a + n + 1);
    long long S = 0, ans = 2e18;
    for (int i = 1; i <= n; i ++) S += p[i];
    for (int x = 0; x <= n; x ++)
        S += a[x], ans = min(ans, S - c * x * (x - 1) / 2);
    cout << ans << '\n';
    return 0;
}