OO第一单元总结

OO第一单元总结

目录

• OO第一单元总结
  • 0 基于度量分析程序结构
    • 0.1 方法与类的复杂度分析（Complexity Metrics）
      • 0.1.1 方法
      • 0.1.2 类
    • 0.2 类之间的依赖度分析（Dependency Metrics）
  • 1 第一次作业
    • 1.1 思路
    • 1.2 度量
    • 1.3 bug
  • 2 第二次作业
    • 2.1 思路
      • 2.1.1主要架构
      • 2.1.2 递归下降
      • 2.1.3 化简与输出
    • 2.2 度量
    • 2.3 bug
  • 3 第三次作业
    • 3.1 思路
    • 3.2 度量
    • 3.3 bug
  • 4 一些感想
  • 5 参考与引用

0 基于度量分析程序结构

使用IDEA的MetricsReloaded工具对程序结构进行分析。工具中可能使用到的参数说明如下：

0.1 方法与类的复杂度分析（Complexity Metrics）

0.1.1 方法

• ev(G)：即 Essential Complexity ，用来表示一个方法的结构化程度，范围在[1,v(G)]之间，值越大则程序的结构越“病态”。

• iv(G)：即 Design Complexity ，用来表示一个方法和他所调用的其他方法的紧密程度，范围在[1,v(G)]之间，值越大联系越紧密。

• v(G)：即循环复杂度，可理解为穷尽程序流程每一条路径所需要的试验次数。

0.1.2 类

• OCavg：表示类的方法的平均循环复杂度

• WMC：表示类的方法的总循环复杂度

0.2 类之间的依赖度分析（Dependency Metrics）

• Cyclic：指和类直接或间接相互依赖的类的数量，这样的相互依赖可能导致代码难以理解和测试
• Dcy， Dcy*： 计算了该类直接依赖的类的数量，带 * 表示包括了间接依赖的类
• Dpt，Dpt*：计算了直接依赖该类的类的数量，带*表示了包括了间接依赖的类

1 第一次作业

1.1 思路

第一次作业比较简单，将读入的字符串进行预处理后（去掉空白字符以及将 ** 转化为 ^ ）按照项的组成正则表达式进行截取，截取后的字符串传入 Term 类的构造方法中，根据 * 对项中字符串进行分割，分析获得项中每一个因子的数据。类图如下：

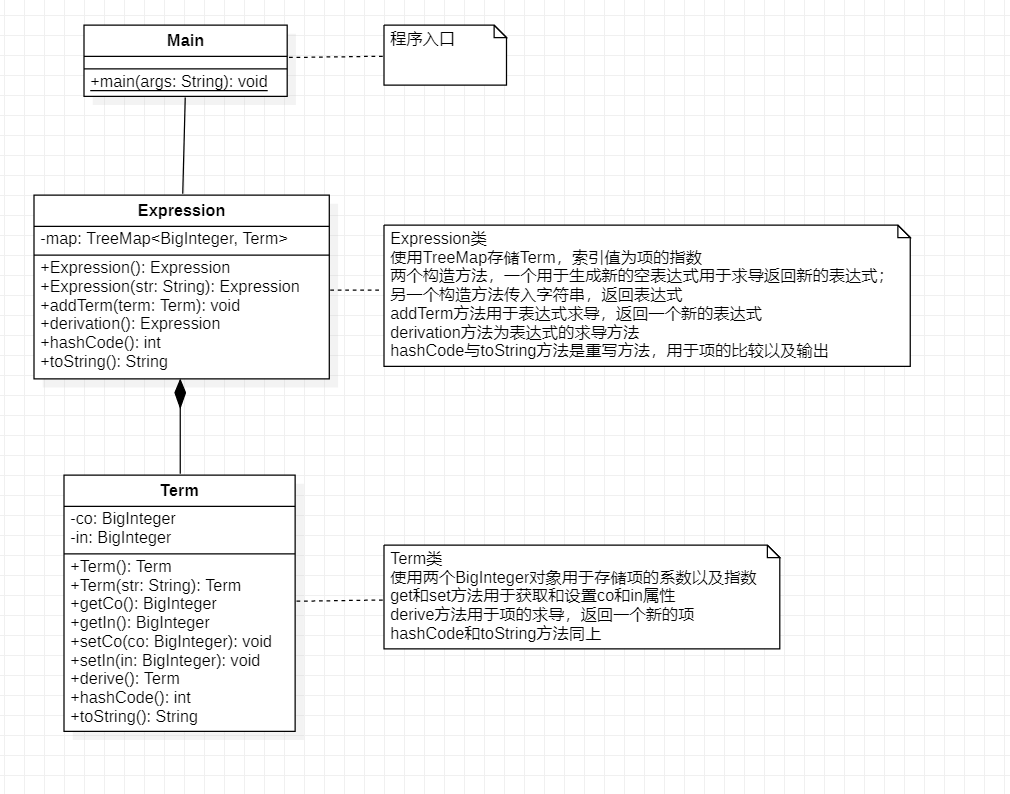
Expression 类和 Term 类是参考第一次实验构造的。由于第一次作业项中只有关于x的幂因子以及常数因子，因此 Term 的成员变量设置了系数和指数，这样在读入字符串进行分析时便可以做到化简。Expression 类则设置了 TreeMap 的结构存储 Term 对象，并使用 Term 对象中的指数成员作为索引值。由于各个类的建立有了好的参考，因此我在第一次作业中的最大难点就是建立合适的正则表达式进行项与因子的解析。在求导部分，只需按照正常的求导公式运算即可。需要注意的是，在求导时我没有进行特殊化处理，系数为 0 的项求导后系数变为 -1 ，这显然是错误的，因此我也参考了第一次实验中的代码，在对所有项进行求导后，去除所有系数为 0 的项。

结果的输出也参考了第一次实验的要求，将指数进行排序后从小到大的顺序输出。可是这样忽略了一点：指数最低的项的系数可能是负的，这样的输出结果会多输出一个 -，导致性能分下降（虽然这与后两次作业相比起来根本就是鸡蛋缝里挑骨头）。

1.2 度量

对程序结构进行度量结果如下：

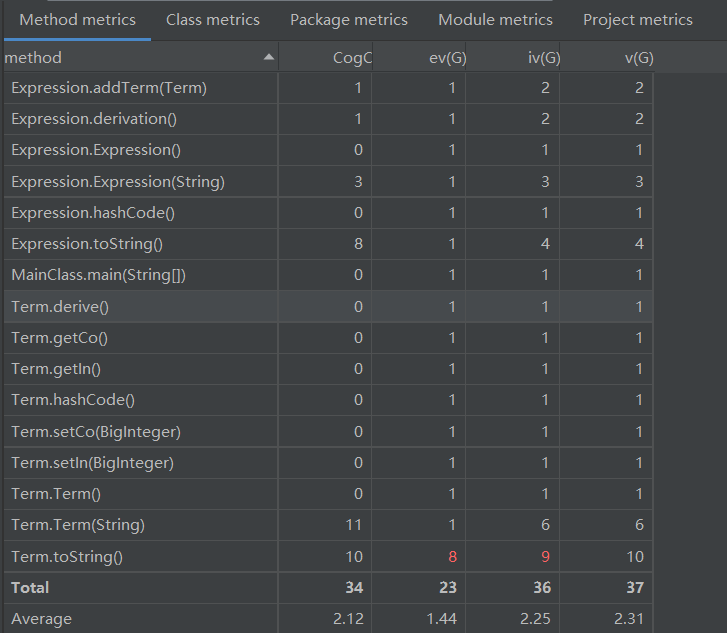
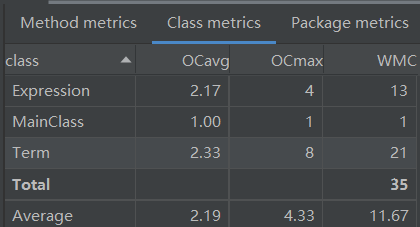
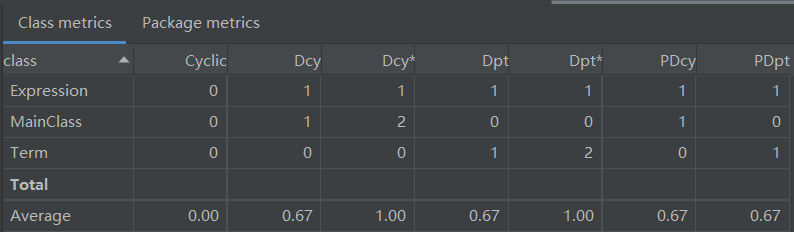
从以上数据可以看出，由于第一次作业结构较简单，且项目的架构参考了第一次实验（前人栽树，后人乘凉），同时采用较为直观的正则表达式分析字符串，因此方法与类的复杂度都不高。

1.3 bug

第一次作业自己的程序并未出现 bug，同时在互测中也没有 hack 出他人的 bug。在互测结束后查看他人的hack 记录时发现 hack 成功的是针对 BigInteger 的测试以及项的数量过多是否会导致“爆栈”的测试。这也给了我接下来几次作业中互测的启示：要针对边缘数据进行 hack 才有检测出他人 bug 的机会。

在第一次作业中，由于数据形式较为简单，因此采用手动构造数据并进行测试的方法。

2 第二次作业

2.1 思路

2.1.1主要架构

第二次作业相对于第一次作业加入了三角函数以及表达式因子，难度陡然加大，对于我来说也是这三次作业中最难的一次。

加入三角函数以及表达式因子意味着第一次作业利用正则表达式进行项与因子的分析的架构完全不适用，项类只有指数和系数的设计方法也必须完全摒弃。重构势在必行。

恰逢第二周的研讨课上有同学提出了利用递归下降方法对字符串进行解析的方法，也有同学分享了接下来的作业的架构分享，因此最终我采用了递归下降的方法对字符串进行解析。表达式类 Exp 与项类 Term 仍保留，但其作用已发生变化，两者均用 ArrayList 存储下一级对象。同时新建 Term 下一级类 Factor 类，此类的成员变量为该因子指数 index 以及该因子类型 obj。因子类型为 Obj 类，子类包括 Const 常数类、Var x 变量类、Sin sin(x) 类、Cos cos(x) 类以及 Exp 类（针对表达式因子）。这些子类中除 Exp 类外，Const 类包括一个成员变量 value，其为常数因子的值；其余的类均无成员变量，仅作为一种标识符。架构的类图如下所示：

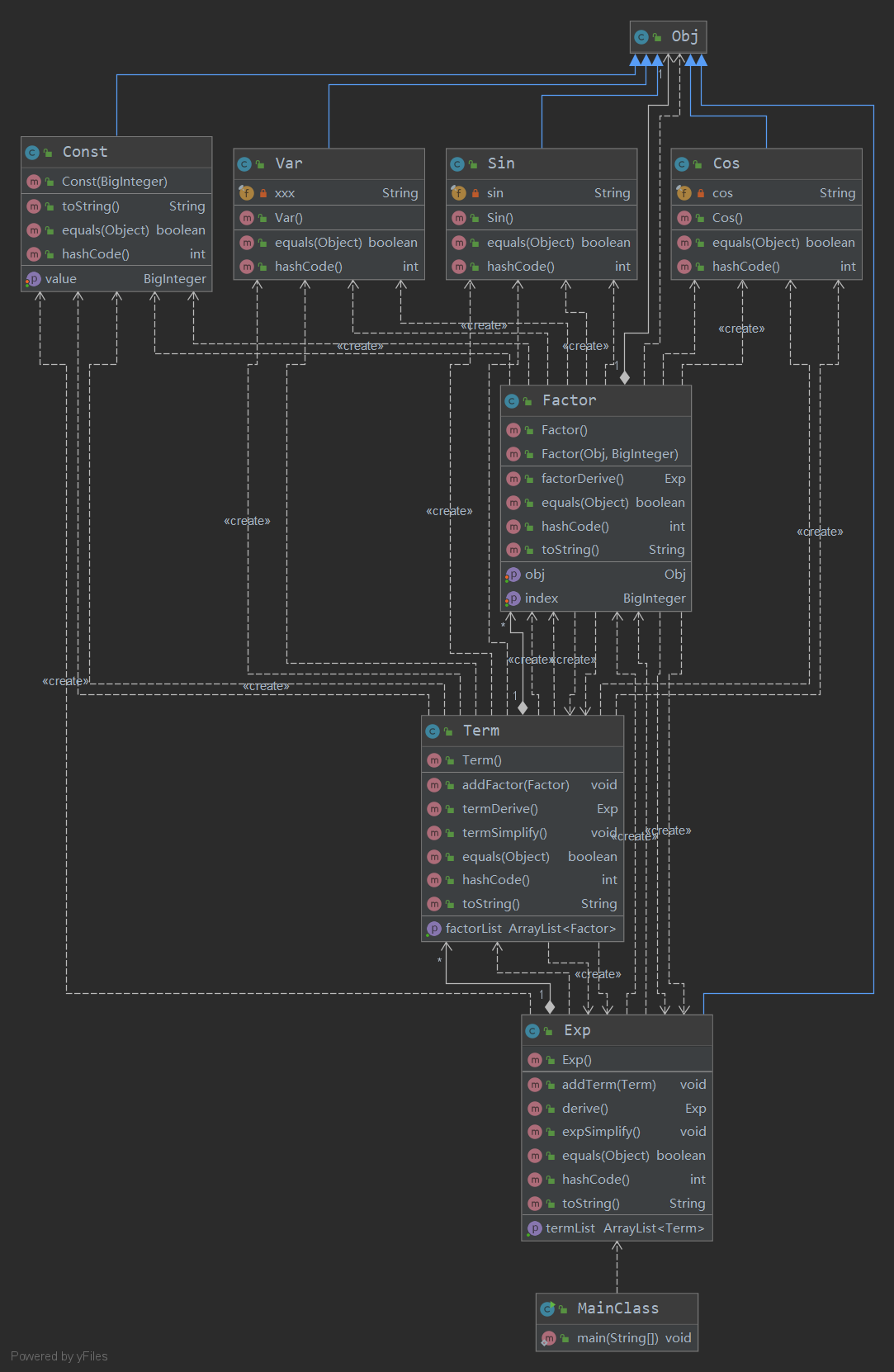
很显然，这里面存在着一种递归调用的关系，比如某个 Exp 对象中含有一个 Term 对象，这个 Term 对象中有一个 Factor 对象，而这个 Factor 对象的 obj 是一个 Exp 对象。这虽然有点费解，却也不难理解。

在我看来，这样的架构有了一点点的面向对象的味道，也能配合递归下降的方法进行使用，因为递归下降就是把表达式中的每一个成分分析出来，这样正好可以返回不同的类。

2.1.2 递归下降

使用递归下降对表达式解析是一项复杂的工作，因此我将这个过程封装为单独的一个 Parse 类，它包括一个 public 的 ParseExp 方法 以及其他均为 private 的 Parse 方法，且由于需要在 main 方法里使用，因此均为 static。同时，递归下降方法需要一个全局性的对于字符串的当前下标，因此创建了 index 成员变量。具体如下：

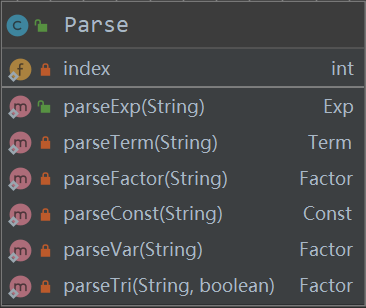
递归下降的具体思路不再阐述，在此其中一个重要的问题是递归如何终止。在这个过程中，我认为广义上的因子是终止的因素，因此返回的最低层次的类为 Factor。

2.1.3 化简与输出

此次作业引入了表达式因子以及由此带来的括号，让化简成为求导结果的重要一环。不过我并没有花费太多时间在这上面，我主要追求的是结果的正确性。不过为了结果不那么臃肿，做了适当的化简，如一个项中相同类型因子的化简、包含常数 0 项的清除、嵌套括号的表达式因子的括号去除等。输出则利用 toString 方法，从低层次类到高层次类一步步输出。这样的结果是性能分还过得去。

2.2 度量

对程序结构进行度量结果如下：

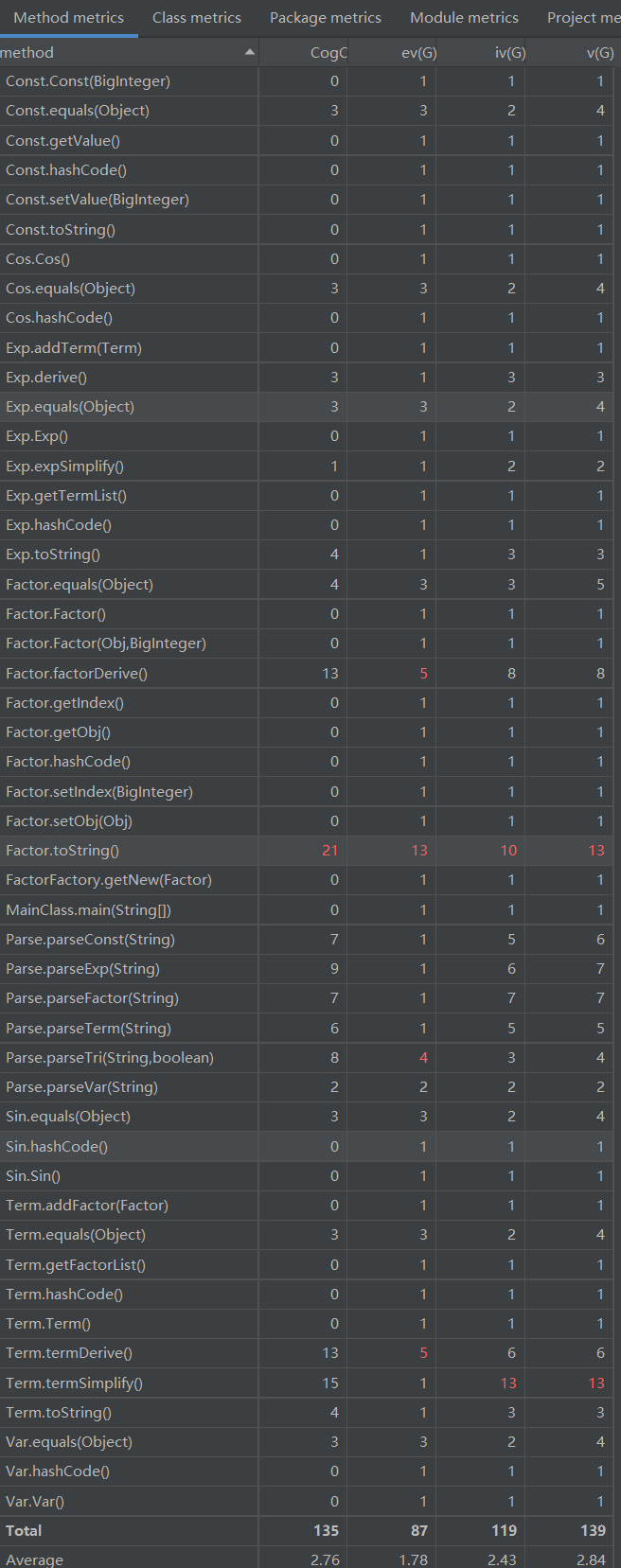
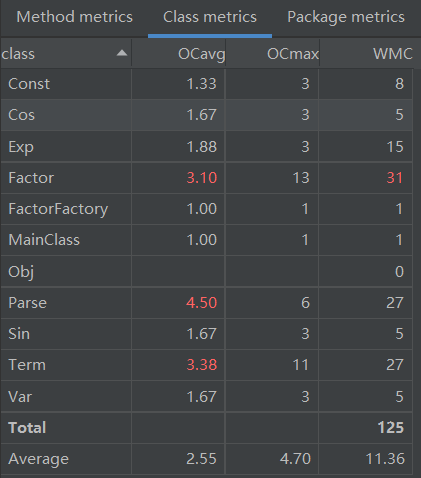
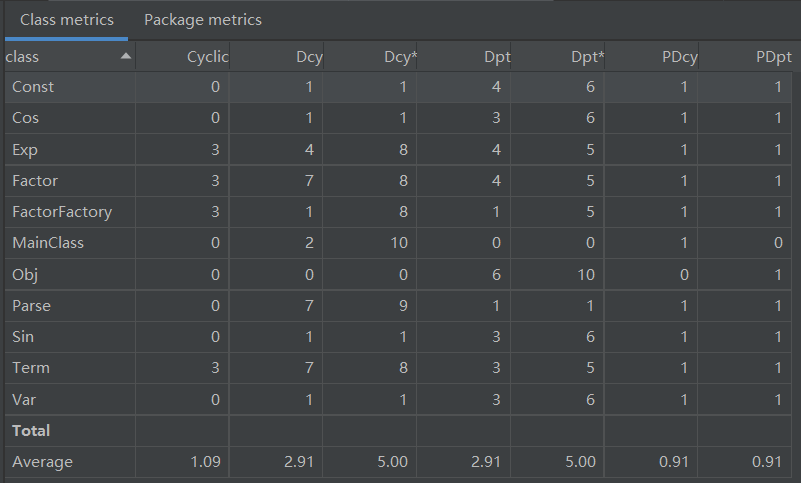
由以上数据可以看出，Factor 类的 toString 方法比较复杂，这是因为调用了太多 Obj 类的对象判断；Term 类的化简方法也较为复杂，也是因为调用了太多 Obj 类的对象判断。从类的层次看，由于存在一定的递归情况，Term，Factor，Parse 类的复杂性比较高。对于类之间的依赖性，由于主体架构比较好，因此耦合度较低。

2.3 bug

本次作业自己的程序没有出现bug，主要是因为在和舍友一起测试时将各种“丑陋”的数据都测试了一遍，找出了出现的bug并修改。在互测中，由于贯彻了“边缘数据”思想，也成功 hack 到了其他同学。

总的来说，这次作业中出现bug主要是在读入和化简的过程中出了问题。在我的房间中，有一位同学对于求导为 0 的结果没有输出，但他对于其他的输出结果的表现是令我仰慕的。有一位同学对于 BigInteger 类型的读入出现了问题；还有一位同学对于连续的正负号以及括号的分析出现了问题。

由于本次作业输出形式比较复杂，用人工比较的方式效率太慢，因此在与同学的合作下写了一个 python 程序，用于分析程序输出结果与标准的结果是否恒等。

3 第三次作业

3.1 思路

第三次作业相对于第二次作业，在表达式的组成上只是新增了允许在三角函数内进行因子的嵌套，因此第二次作业的架构完全可以沿用下来，只需在 Sin 类和 Cos 类中添加一个 Factor 类型的成员即可，修改一下求导方法、化简方法以及输出方法。具体类图如下：

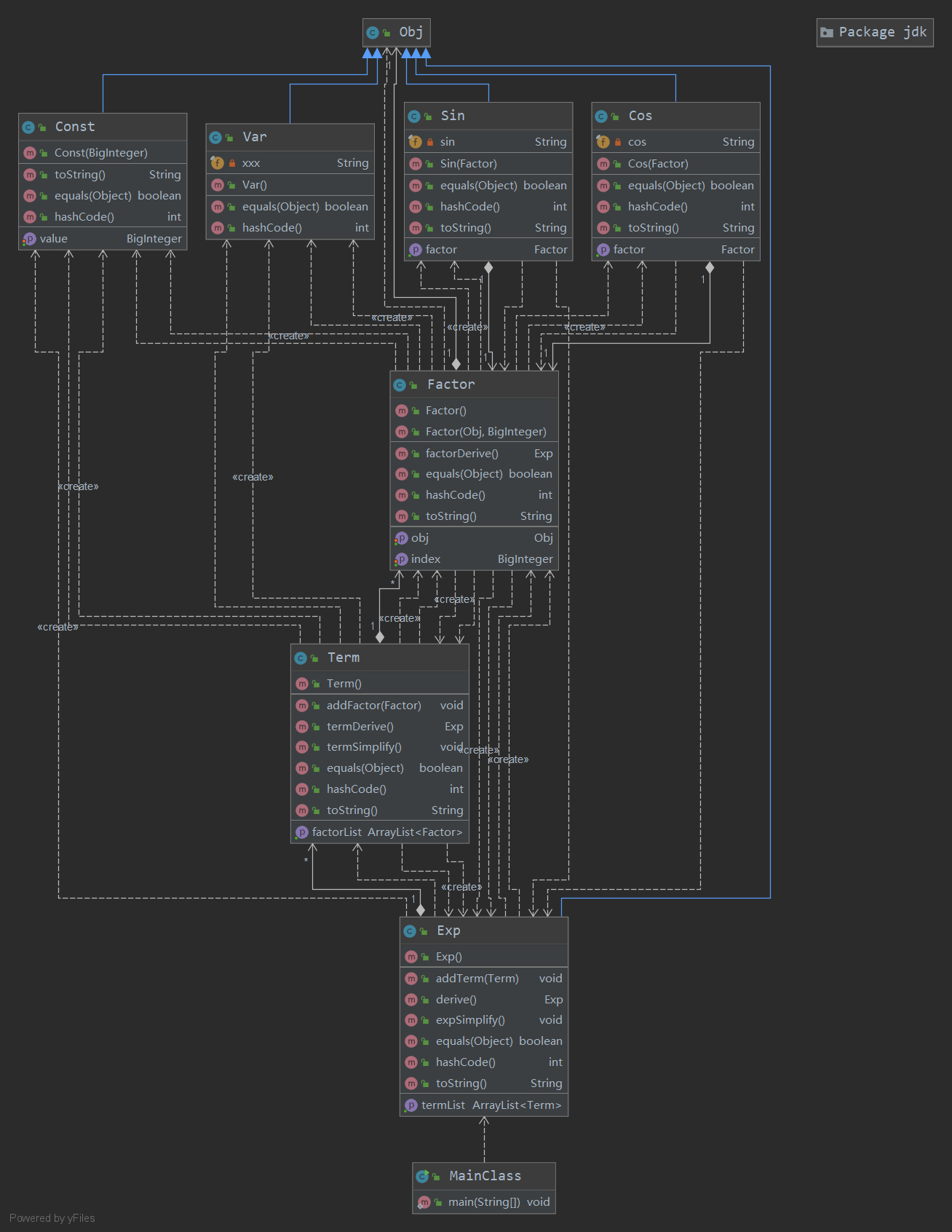
同时，在第三次作业中要求对输入的表达式进行格式检查。由于在第二次作业时就听闻需要进行格式检查的要求，而递归下降方法在解析表达式的同时可以顺便完成格式检查，因此我只需在 Parse 类的各个方法中针对不同组成的格式要求，添加一些判断条件即可完成格式的检查。这也是我采用递归下降解析表达式而不是表达树的原因。

3.2 度量

对程序结构进行度量结果如下：

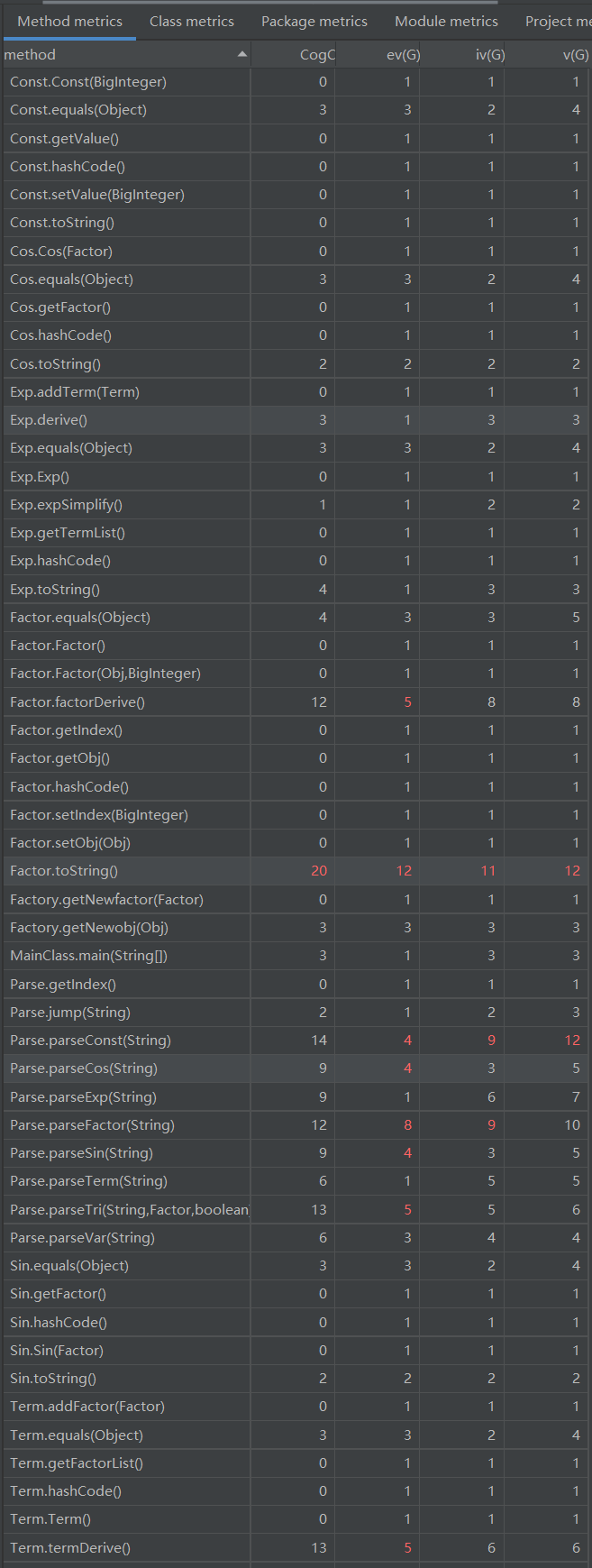
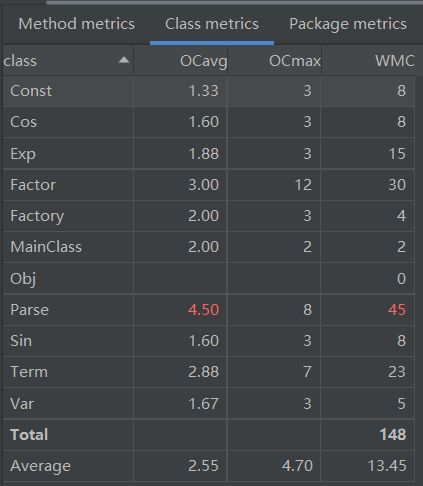
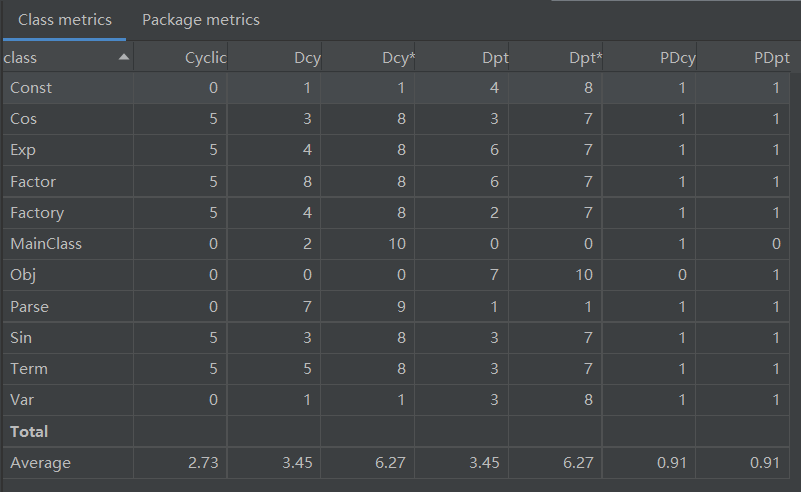
由数据可以看出，由于第三次作业加入了更多了嵌套规则以及格式检查的要求，parse 方法的复杂度均有一定程度的提高；相应地，Parse 类的复杂度也提高了不少。

3.3 bug

第三次作业由于修改的内容不多，因此也没有出现 bug。在互测中，我发现有一位同学对于某些正确的输入输出了 WF，可能是忽略了某些判断情况。还有一位同学对于连续的负号加括号的分析出现了问题，导致输出错误。在房间中还有一位同学的 bug 我没有发现，是 sin 或 cos 中的因子为 0 的情况。只能说手动构造数据的方法还是无法应对越来越复杂的规则。

对于输出结果的判断和分析仍然采用同第二次作业的方法。不过这次我先将需要测试的程序进行打包，再统一运行，这样可以达到一次测试所有程序的效果，互测效率也有了较大的提高。

4 一些感想

能够顺利通过第一单元的三次作业，确实是个不小的挑战。从一开始面对作业要求不知所措，到后来一点点写出代码，再到对整个项目进行重构，到最后不断通过弱测、互测、强测，成功 hack，这就像坐过山车一样。同时，面向对象的思想也逐渐在我的头脑中扎根下来，这为接下来的学习奠定了一个好的基础。

但是遗憾也是有的。比如在输出结果的化简上没有花费太多的功夫，导致第三次作业的性能分平均接近为 0。希望在之后的作业能够更多地挑战自己，在性能上做到更好。在这几次作业中我也感受到在 java 中还有很多知识是我还没有接触到的，我需要花费更多的时间去学习这些知识，以优化我的开发过程。

5 参考与引用

2019_BUAAOO_第一单元总结 - since_AUG - 博客园