洛谷P1875佳佳的魔法药水题解

这是一道很好的最短路的题目

---

难点

1.如何建图
2.如何进行更新最短路
3.求最小方案

---

建图

输入中有药水的配置
A + B = C

1 2 0 
4 5 1 
3 6 2

这看上去是不是很像图论?
选用链式前向星
如下

int head[1010],cnt;
void add(int u,int v,int w){
	E[++cnt].to = v;
	E[cnt].w = w;
	E[cnt].next = head[u];
	head[u] = cnt;
}

和

int u,v,w;
while(scanf("%d%d%d",&u,&v,&w)!=EOF){
	add(u,v,w);
	if(u==v)	continue;
	add(v,u,w);
}

诶,这看上去和模板也没什么区别啊?

先放下建图.

---

求最小方案数

用cost数组记录某药水的最小值,ans数组记录某药水的方案数量
cost初始化为商店药水原价,ans初始化为1(题目中:直接买0号药水)
诶?多少种不同的花费最少的方案,乍看好想好难啊,但细细想想挺简单的,来,上图!!!(这不是本题的建图,只是为了方便理解)

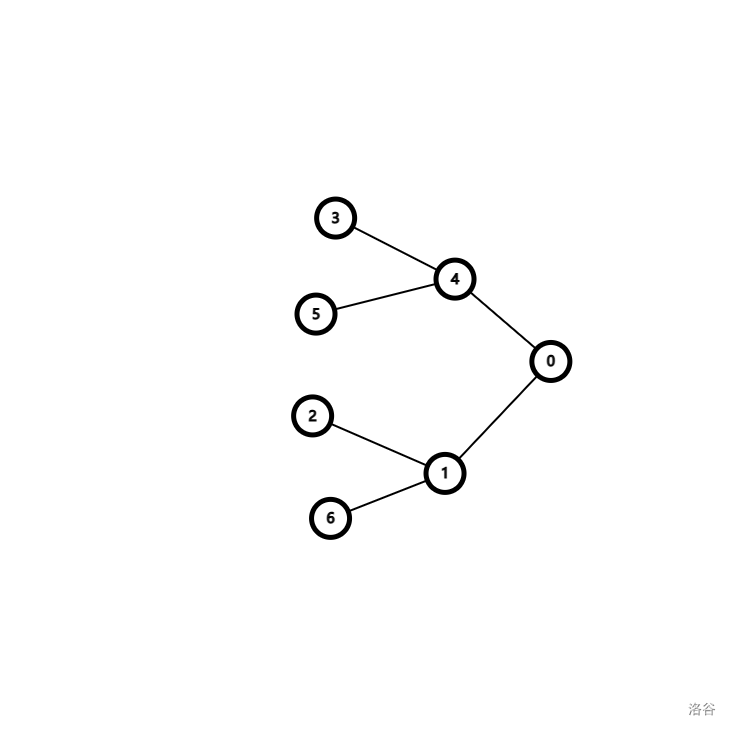
假设配置4有两种方案,3->4 和 5->4,配置1有两种方案2->1和6->1,那么配置0有4种方案:
3->4->0
5->4->0
2->1->0
6->1->0
诶,那这么说配置0不就是有2 * 2种方案?

ans[c] = ans[a]*ans[b];

这是对应当原来配置0的方案不是最小方案,那么如何原来配置0也是最小方案呢?

ans[c] += ans[a]*ans[b];

加上不就好了吗

---

更新最短路

这里选用dijkstra来更新最短路
一般的dijkstra都是从源点出发,然后到其他点的最短路径。但这是道蓝题,肯定不一般。依据图的建立可知,这道题没有固定源点。
然后看看题目,诶!输入中有所有药水在魔法商店的价格。那么,我们是不是可以从最小的价格的药水开始考虑最小价值?
这里用优先队列实现

priority_queue<pair<int,int> , vector<pair<int,int> > , greater<pair<int,int> > >q;

pair为数对,储存价格和位于商店第几个
这是,重点来了————
我们要更新!!!
如何更新,也就是怎样才能让佳佳得到0号药水花费最小,(这佳佳也太穷了吧)
不就是用小的药水的价钱来配置大的药水的价钱吗?
那两瓶小的药水我们是不是要知道价格才能更新啊?所以是在已知中更新最小值,那么就必须保证两瓶都被访问过,这就需要vis数组了。先从q中取出一瓶药,标记已访问,然后在去魔法书里找一找有没有可配置的配方,这就和之前的图联系上。
边权记录的是两瓶药混合后得到的药,这不就排上用场了吗?
具体代码如下

for(int i = head[u];i;i=E[i].next){
	int b = E[i].to,w = E[i].w;//存图是,w相当于c 
	//保证a,b两点都被访问 
	if(vis[b]){
		if(cost[w]>a + cost[b]){
			ans[w] = ans[u]*ans[b];//因为原方案不是最小方案 
			cost[w] = a + cost[b];//是不是很像题目中的 A+B=C?
			q.push(make_pair(cost[w],w));
			}else if(cost[w] == a + cost[b]){//原来的方案数再加上另外的 
				ans[w] += ans[u]*ans[b];
				}
			}
		}

到这,应该就能懂为什么那样建图。

---

AC code :

#include<iostream>
#include<queue>
#include<vector>
using namespace std;
struct edge{
	int to,next,w;
}E[1000001];
int head[1010],cnt;
void add(int u,int v,int w){
	E[++cnt].to = v;
	E[cnt].w = w;
	E[cnt].next = head[u];
	head[u] = cnt;
}

int cost[1010],vis[1010],ans[1010];
priority_queue<pair<int,int> , vector<pair<int,int> > , greater<pair<int,int> > >q;
void dijkstra(){
	//这没有固定的源点 
	int tot = 0;
	while(!q.empty()){
//		cout <<tot++ << " ";
		int a = q.top().first,u = q.top().second; 
		q.pop();
		//已经被更新 
		if(a!=cost[u]){
			continue;
		}
		vis[u] = 1;
		for(int i = head[u];i;i=E[i].next){
			int b = E[i].to,w = E[i].w;//存图是,w相当于c 
			//保证a,b两点都被访问 
			if(vis[b]){
				if(cost[w]>a + cost[b]){
					ans[w] = ans[u]*ans[b];//因为原方案不是最小方案 
					cost[w] = a + cost[b];//是不是很像题目中的 A+B=C?
					q.push(make_pair(cost[w],w));
				}else if(cost[w] == a + cost[b]){//原来的方案数在加上另外的 
					ans[w] += ans[u]*ans[b];
				}
			}
		}
	}
}

int main(){
	int n;
	scanf("%d",&n);
	for(int i = 0;i<n;i++){
		scanf("%d",&cost[i]);
		ans[i] = 1;//直接买 0号药水
		q.push(make_pair(cost[i],i));
	}
//	for(int i = 0;i<n;i++){
//		printf("%d",q.top().first);
//		q.pop();
//	}
	
//	return 0;
	int u,v,w;
	while(scanf("%d%d%d",&u,&v,&w)!=EOF){
		add(u,v,w);
		if(u==v)	continue;
		add(v,u,w);
	}
	dijkstra();
	printf("%d %d",cost[0],ans[0]);
	return 0;
}