题解 SP913 【QTREE2 - Query on a tree II】

树剖解法

题解区写树剖的只有两篇，而且这两篇求 \(\texttt{DIST}\) 都是 \(\mathcal O(\log n)\) 的做法，其实可以 \(\mathcal O(1)\) 求出。

前置芝士

用重链剖分AC LCA模板 和 树上k级祖先模板。

Solution

首先对整棵树进行树剖，即两次 \(\texttt{dfs}\)，但是在此过程中，需要多记录一个变量，dist[u]，即u节点到根节点的距离，用其父亲的 dist 加上边权即可，以便 \(\mathcal O(1)\) 求 \(\texttt{DIST}\)。

复杂度 \(\mathcal O(n)\)

DFS Code

void dfs1(int u,int f){
    siz[u]=1;fa[u]=f;//记录子树大小、父亲
    dep[u]=dep[f]+1;//记录深度
    int maxs=-1;
    for(auto &x:e[u]){//C++11写法
        int v=x.to,w=x.w;
        if(v==f)continue;
        dist[v]=dist[u]+w;//一定不能在dfs子节点后求dist，因为这样儿子没求先求了孙子
        dfs1(v,u);
        siz[u]+=siz[v];
        if(siz[v]>maxs){
            son[u]=v;//记录重儿子
            maxs=siz[v];
        }
    }
}
void dfs2(int u,int f){
    id[u]=++tot;//记录新编号
    dfn[tot]=u;//编号映射
    top[u]=f;//记录重链的顶端
    if(!son[u])return;
    dfs2(son[u],f);
    for(auto &x:e[u]){
        int v=x.to;
        if(id[v])continue;
        dfs2(v,v);
    }
}

接下来是 \(\mathcal O(1)\) 求 \(\texttt{DIST}\) 了！

注意到一个性质：real_dis(u,v)=dist[u]+dist[v]-2*dist[lca(u,v)]

（real_dis=真实距离，待会还有相对距离）

可以用一张图来理解：

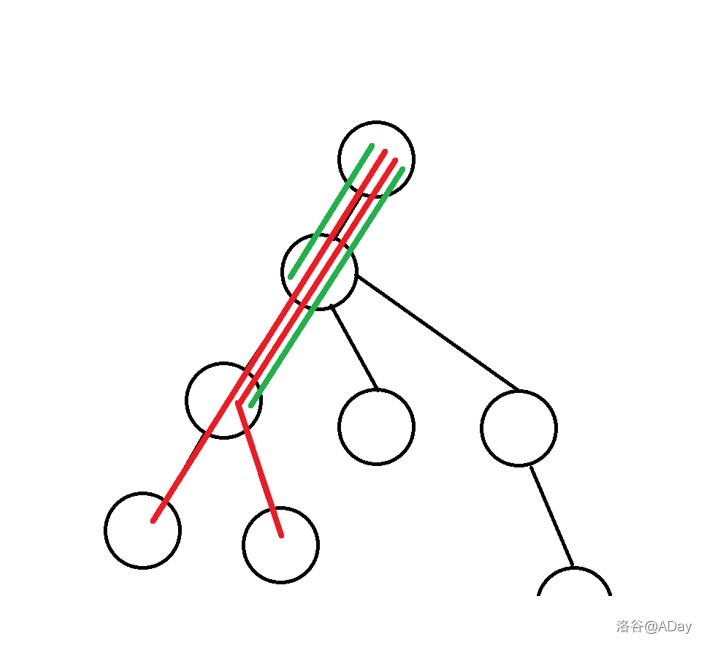
没错这就是lxl的图

然后直接运算就完了。。。

DIST Code

il int lca(int u,int v){
    for(;top[u]!=top[v]&&u!=rt;u=fa[top[u]])
        if(dep[top[u]]<dep[top[v]])swap(u,v);
    return dep[u]<dep[v]?u:v;
}//见P3379
il int real_dis(int u,int v){return dist[u]+dist[v]-2*dist[lca(u,v)];}

最后是 \(\mathcal O(\log n)\) 求 \(\texttt{KTH}\)

我们要用到相对距离，即假设边权为 \(1\) 时的真实距离，用于求两点间节点个数。和真实距离同理，rela_dis(u,v)=dep[u]+dep[v]-2*dep[lca(u,v)]，此时只要判断第k个节点在LCA的左边还是右边，就能把问题转化成求u的k级祖先或者v的rela-k级祖先。

KTH Code

il int kth(int u,int k){
    for(;id[u]-id[top[u]]<k;u=fa[top[u]])
        k-=dep[u]-dep[top[u]]+1;
    return dfn[id[u]-k];
}//见P5903
...
scanf("%d%d%d",&x,&y,&z);z--;
int dis=rela_dis(x,y),LCA=lca(x,y);
if(rela_dis(x,LCA)>=z)printf("%d\n",kth(x,z));
else printf("%d\n",kth(y,dis-z));

完结撒花~