题解 P3076 【[USACO13FEB]Taxi G】

前天 \(\texttt{zwj}\) 老师 在 \(\texttt{贪心}\) 专题讲了这道题，特此水一篇题解。

（其实是因为一个多月没写题解了，感觉社区分会掉下70）

先以样例为例子来看看：

（但为了突出其某些性质，把 \(s1\) 改为了 \(2\)，但其答案不变）

\(\texttt{Bessie}\) 从 \(0\) 号站到 \(2\) 号站接第 \(1\) 个客户（\(2\) 站），从 \(2\) 号站出发到 \(6\) 号站（\(4\) 站），放下第 \(1\)个客户，接第 \(2\) 个客户，送到 \(5\) 号站再回来（\(2\) 站），再接第 \(1\) 个客户，送到 \(9\) 号点（\(3\) 站），然后自己走到 \(10\) 号点（\(1\) 站），共 \(12\) 站。

那么画出图来是这样的（\(p_1->p_8\)）：

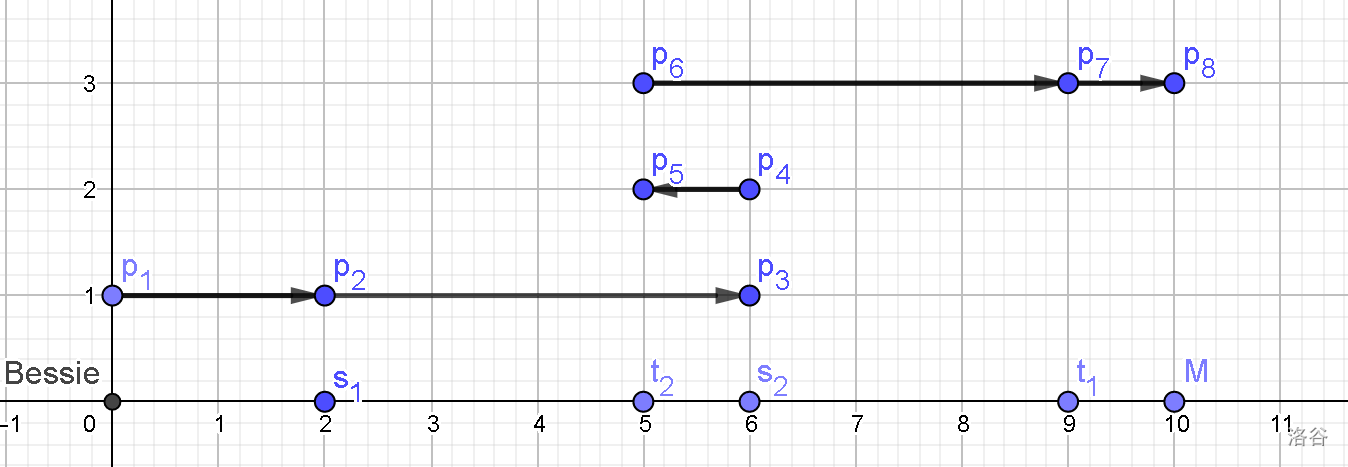
我们不难发现，\(\texttt{Bessie}\) 走的路程，即 \(ans\)，必然满足 \(ans \ge \sum\limits_{i=1}^n |s_i-t_i|\)。

那么，思考一下，\(ans\) 比 \(\sum\limits_{i=1}^n |s_i-t_i|\) 多出来了什么呢？/yiw

来画个图吧~

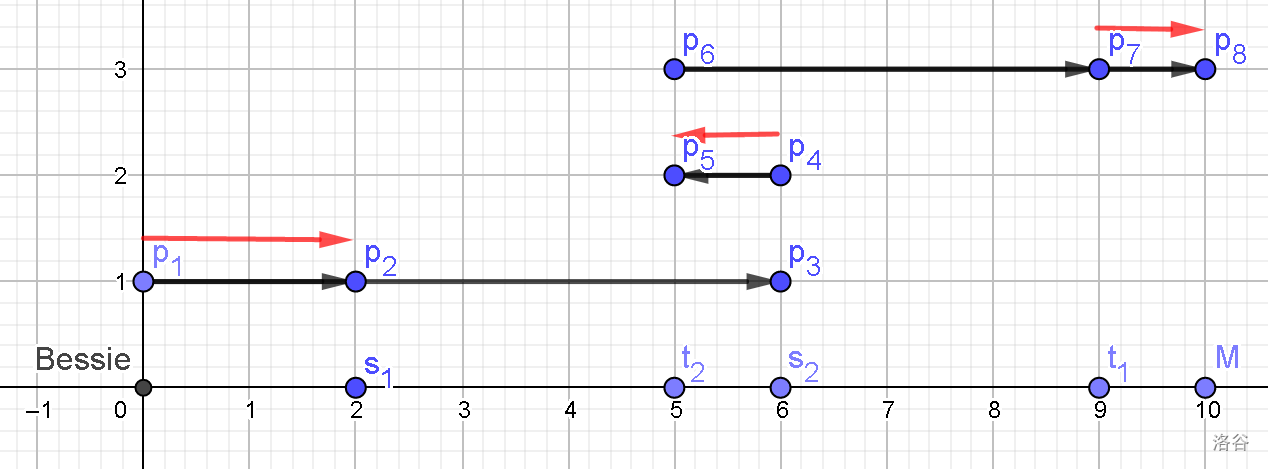
如图，红线即为多出的部分，可能你还是看不出什么。那么我们把 \(\texttt{Bessie}\) 看成一只从 \(M\) 走到 \(0\) 的牛，即 \(s_0->t_0\)

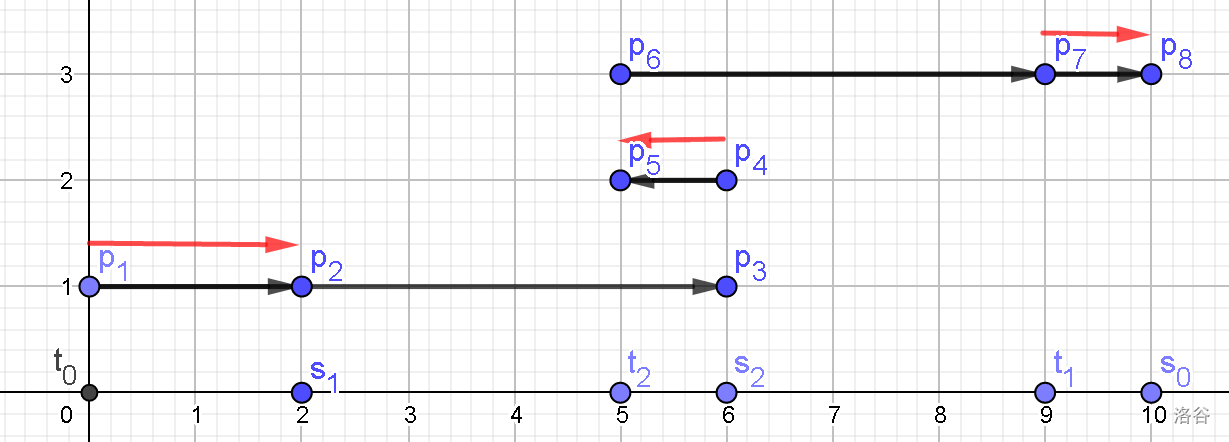
可以发现，红线都是一条 \(s_i\) 到 \(t_j\) 的线，且每个 \(s\) 和 \(t\) 都被包含了，所以 \(ans=\sum\limits_{i=1}^n |s_i-t_i|+\sum |s_i-t_j|\)。又因为 \(\sum\limits_{i=1}^n |s_i-t_i|\) 是定值，我们的任务就是最小化 \(\sum |s_i-t_j|\)。

然后把 \(s\) 和 \(t\) 排序即可。设 \(s,t\) 排序后分别为 \(a,b\) ，则 \(ans=\sum\limits_{i=1}^n |s_i-t_i|+\sum\limits_{i=0}^n |a_i-b_i|\)（别忘了 \(\texttt{Bessie}\) 的路程）。

那么为什么排序相减就最小呢？因为任意交换同数组两个数必然会使结果增大。

\(\texttt{Ugly Code:}\)

#include<bits/stdc++.h>
using namespace std;
#define i64 long long//不开ll见祖宗
namespace io{static streambuf *inbuf=cin.rdbuf();static streambuf *outbuf=cout.rdbuf();char buf[1<<21],*p1=buf,*p2=buf;inline char gc(){return (p1==p2&&(p2=(p1=buf)+inbuf->sgetn(buf,1<<21),p1==p2)?EOF:*p1++);}inline void pc(const char x){static streambuf *outbuf=cout.rdbuf();outbuf->sputc(x);}inline void ps(const char *x){unsigned _len=strlen(x);for(unsigned i=0;i<_len;i++)pc(x[i]);}inline i64 read(){register int _s=0,_f=1;register char _ch=gc();for(;!isdigit(_ch);_ch=gc())if(_ch=='-')_f=-1;for(;isdigit(_ch);_ch=gc())_s=_s*10ll+_ch-'0';return _s*_f;}template<typename T>inline void write(T _x1){if(_x1<0)pc('-'),_x1=-_x1;static char _sta[15];int _p=0;do{_sta[_p++]=_x1%10^48;_x1/=10;}while(_x1);while(_p--)pc(_sta[_p]);}string _s;inline string readstr(){_s.clear();register char _ch=gc();while(isspace(_ch))_ch=gc();for(;!isspace(_ch);_ch=gc())_s+=_ch;return _s;}inline void writestr(const string _s){for(unsigned i=0;i<_s.size();++i)pc(_s[i]);}template<typename T>inline void writeln(const T _x){write(_x);pc(10);}}using namespace io;
//IO优化
const int maxn=1e5+5;
int n,m;
i64 ans,s[maxn],t[maxn];
int main()
{
	n=read();m=read();
	for(int i=1;i<=n;i++)
	{
		s[i]=read();t[i]=read();
		ans+=abs(s[i]-t[i]);//Σ|si-ti|
	}
	s[0]=m;t[0]=0;//Bessie的路程
	sort(s,s+n+1);sort(t,t+n+1);//排序啦
	for(int i=0;i<=n;i++)
		ans+=abs(s[i]-t[i]);//min(Σ|si-tj|)
	writeln(ans);
	return 0;
}