基数排序

基数排序

定义

基数排序（Radix sort）是一种非比较型的排序算法，最早用于解决卡片排序的问题。基数排序将待排序的元素拆分为 𝑘 个关键字，逐一对各个关键字排序后完成对所有元素的排序。

如果是从第 \(1\) 关键字到第 𝑘 关键字顺序进行比较，则该基数排序称为 MSD（Most Significant Digit first）基数排序；

如果是从第 𝑘 关键字到第 \(1\) 关键字顺序进行比较，则该基数排序称为 LSD（Least Significant Digit first）基数排序。

显然 MSD 基数排序比 LSD 基数排序更好理解，并且二者的时空复杂度均相同，但是 MSD 通常需借助递归或迭代来实现，这样既不方便，时间常数也大，因此自然数间的排序更常用的是 LSD 基数排序，我们接下来也只详细介绍 LSD 基数排序。

LSD 基数排序算法流程

前置知识：稳定排序

排序的稳定性是指相等的元素经过排序之后相对顺序是否发生了改变。

算法流程：

将待排序的元素拆分为 𝑘 个关键字，然后先所有元素的第 𝑘 关键字进行稳定排序，再对所有元素的第 \(k-1\) 关键字进行稳定排序，再对所有元素的第 \(k-2\) 关键字进行稳定排序……最后对所有元素的第 \(1\) 关键字进行稳定排序，这样就完成了对整个待排序序列的稳定排序。

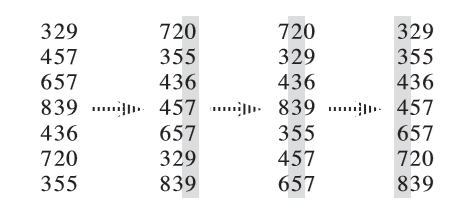
对于 \(\mathtt{int}\) 范围内的自然数而言，我们将一个数十进制的每一位作为关键字，那么 \(k\le 10\) ，每个关键字的值域也很小，只有 \(0\sim 9\)，所以对每个关键字的排序可以采用计数排序或桶排序此类复杂度依赖于值域的稳定排序。

计数排序：

性质

稳定性

每个关键字排序都使用稳定排序，所以基数排序也是稳定的

时间复杂度

对每个关键字的计数排序复杂度为 \(\mathcal O(n+w)\)，其中 \(w\) 为每个关键字的值域，对于自然数排序则可忽略 \(w\)，所以整个排序时间复杂度为 \(\mathcal O(kn)\)。

因此通常而言，基数排序比时间复杂度至少为 \(\mathcal O(n\log n)\) 的基于比较的排序算法（比如快速排序、归并排序）要快。

空间复杂度

显然为 \(\mathcal O(n+w)\)

代码

用计数排序实现内层关键字排序

#include<stdio.h>
#include<math.h>
#include<string.h>
const int N=1e5+5;
int n,k,w;
void counting_sort(int p,int*a,int*b){
	int cnt[10]={0};
	int base=1;
	for(int i=1;i<=p;i++)base*=10;
	for(int i=1;i<=n;i++)cnt[(a[i]/base)%10]++;//计算第p关键字并统计
	for(int i=1;i<=9;i++)cnt[i]+=cnt[i-1];
	//需要空数组b来保存这层关键字排序的结果
	for(int i=n;i>=1;i--){
		int tmp=(a[i]/base)%10;
		b[cnt[tmp]]=a[i];
		cnt[tmp]--;
	}//为保证排序的稳定性，此处循环i应从n到1
    //即当两元素关键字的值相同时，原先排在后面的元素在排序后仍应排在后面
	for(int i=1;i<=n;i++)a[i]=b[i];
}
void radix_sort(int*a,int*b){
	for(int i=0;i<=9;i++)counting_sort(i,a,b);
}
int main(){
	int a[N],b[N];
	scanf("%d",&n);
	for(int i=1;i<=n;i++)scanf("%d",a+i);
	radix_sort(a,b);
	for(int i=1;i<=n;i++)printf("%d ",a[i]);
	return 0;
}