transformer-2
Position Encoding
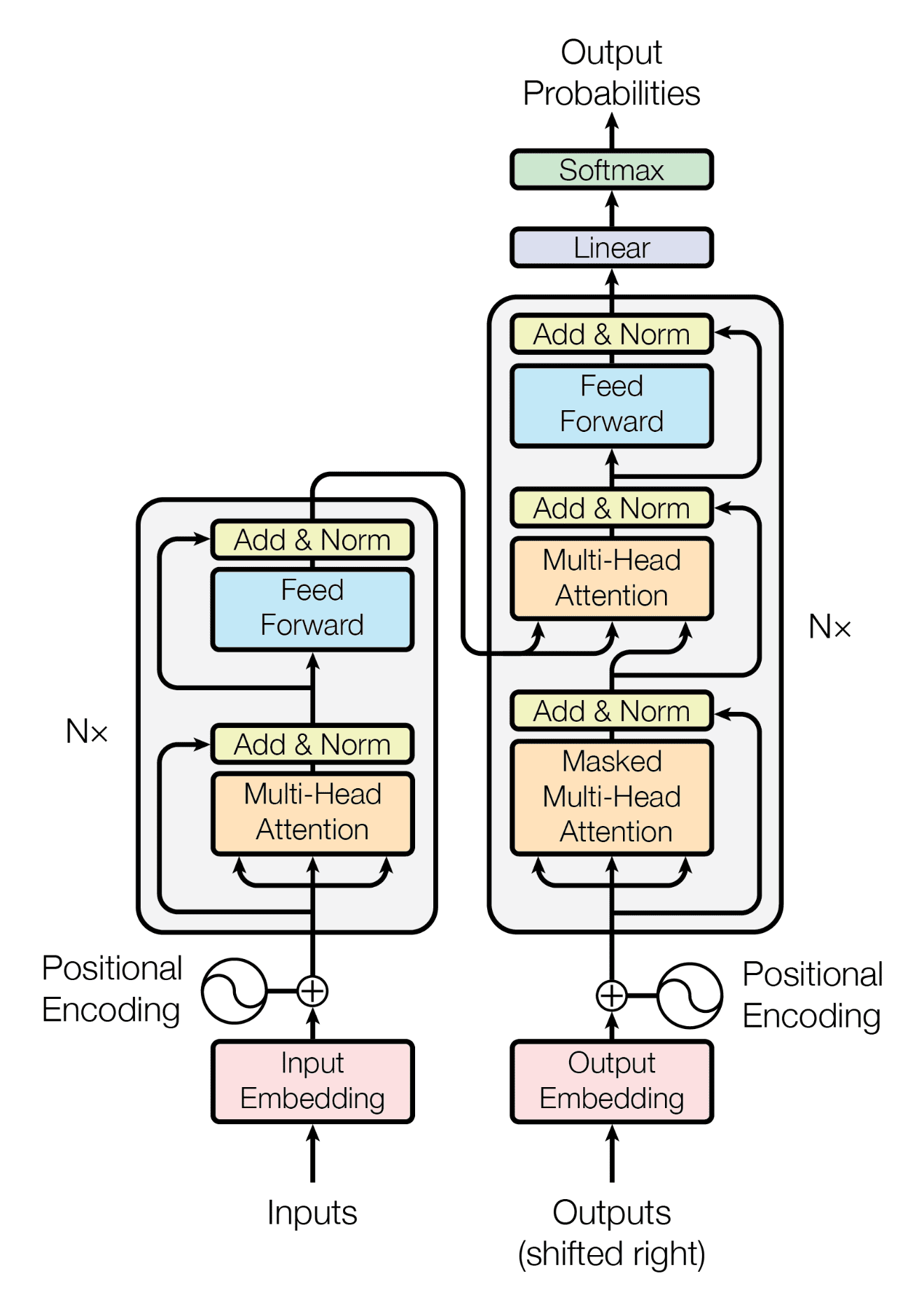
直入主题: \(input=input\_emb+pos\_emb\)
1. 构造Position Encoding 几种方式
一般需要满足:
- 能表示绝对位置
- 不同序列长度,相对位置也要固定
- 具有良好的外推性质
- 按位置自然数递增,第一个位置1,第二个位置2 。。。
- 外推遇到更长的序列无法标记,泛化受影响
- 序列很长时,位置值会越来越大
- 用【0,1】范围值来标记,长度为3就将0~1三等分
- 不同的等分相对距离会变动
- 使用二进制向量标记位置
- 离散编码,不如稠密编码向量
- 周期函数(sin)来表示位置
- \(PE_t=[sin(\frac{1}{2^0}t),sin(\frac{1}{2^1}t),sin(\frac{1}{2^2}t)...,sin(\frac{1}{2^{i-1}}t)...]\)
- i越大,t的变化越不敏感;为避免不敏感问题,所有权重系数都加系数\(w_i\)
- \(PE_t=[sin(\frac{1}{w_0}t),sin(\frac{1}{w_i}t)...,sin(\frac{1}{w_i}t)...]\) \(w_i=\frac{1}{10000^{i/d_m-1}}\)
- 使用sin和cos交替表示
- 使用sin解决了:
- 泛化性的问题,也即能够很好的应对未见过的序列
- 使用向量表示,而且向量在有界空间内
- 位置向量是否能够线性变化,如此也能表示相对位置
- \(PE_{t+\Delta t} = T_{\Delta t} * PE_t\) 不妨使用三角变换式:\(\begin{pmatrix} sin(t+\Delta t ) \\ cos(t+\Delta t) \end{pmatrix}\) = \(\begin{pmatrix} cos(\Delta t) & sin(\Delta t) \\ -sin(\Delta t) & cos(\Delta t) \end{pmatrix}\) \(\begin{pmatrix} sin(t) \\ cos(t) \end{pmatrix}\)
- 使用sin解决了:
\[\begin{aligned}
PE_{t+\Delta t} = T_{\Delta t} * PE_t &= \begin{pmatrix}
\begin{bmatrix} cos(w_0\Delta t) & sin(w_0\Delta t) \\ -sin(w_0\Delta t) & cos(w_0\Delta t) \end{bmatrix} & \cdots & 0 \\
\vdots & \ddots & \vdots \\
0 & \cdots & \begin{bmatrix} cos(w_{d_m/2-1}\Delta t) & sin(w_{d_m/2-1}\Delta t) \\ -sin(w_{d_m/2-1}\Delta t) & cos(w_{d_m/2-1}\Delta t) \end{bmatrix}
\end{pmatrix} \begin{pmatrix}
sin(w_0\Delta t) \\
cos(w_0\Delta t) \\
\vdots \\
sin(w_{d_m/2-1}\Delta t) \\
cos(w_{d_m/2-1}\Delta t)
\end{pmatrix}
\\ &= \begin{pmatrix}
sin(w_0(t+\Delta t)) \\
cos(w_0(t+\Delta t)) \\
\vdots \\
sin(w_{d_m/2-1}(t+\Delta t)) \\
cos(w_{d_m/2-1}(t+\Delta t))
\end{pmatrix}
\end{aligned}
\]
通过如下线性变换容易将\(PE_t\) 转变成\(PE_{t+\Delta t}\)
2. 位置编码可视化
transformer中使用的就是交替编码:
\[PE_t=[sin(\frac{1}{w_0}t),sin(\frac{1}{w_i}t)...,sin(\frac{1}{w_i}t)...] \\ w_i=\frac{1}{10000^{i/d_m-1}} \\
i=0,1,\cdots,d_{m/2}-1 \\
\]
假设每个向量维度为512,那么则有256组
看看可视化图:
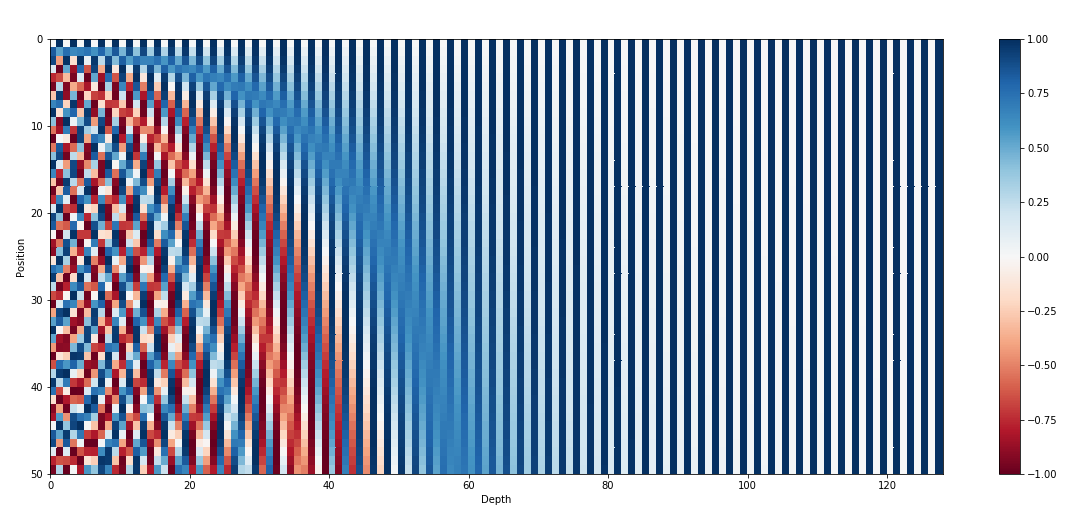
向量的低纬度变化剧烈,取值变化大,高维度变化不明显,取值都在[-1,1]之间。
3. 位置编码性质
- 两个位置编码乘积取决于偏移量
\[\begin{align}
PE_t^T*PE_{t+\Delta t}^T &= \sum_{i=0}^{d_m/2-1}[sin(w_it)sin(w_i(t+\Delta t)) + cos(w_it)cos(w_i(t+\Delta t))] \\
&= \sum_{i=0}^{d_m/2-1}cos(w_i(t-(t+\Delta t))) \\
&= \sum_{i=0}^{d_m/2-1}cos(W_i\Delta t)
\end{align}\]
- 位置编码的点积无向
- \(PE_t^T*PE_{t+\Delta t}^T = PE_t^T*PE_{t-\Delta t}^T\)
- 根据性质1可以知,说明这种类型的位置编码可以表示相对距离,无法表示方向
- pos encoding 进入attention层,\(PE_t^TW_Q^TW_KPE_{t+k}\)可能会失去内积性质



 浙公网安备 33010602011771号
浙公网安备 33010602011771号