AGC059B 题解

对于一种构造，考虑怎么表示。

可以把相邻不同颜色建图连边。

注意到答案不可能小于 \(n-1\)，否则图不联通，显然不可能。

考虑什么情况下是 \(n-1\)。图是一棵树。

考虑怎么构造出一棵树。

因为一种颜色出现次数大于等于这个点的度数，可以考虑可以确定叶子。

把剩余度数最小的往最大的连边，如果出现两个剩余度数为 1 的连边，说明不可能是树。否则是树。

怎么通过树构造原来的颜色序列？

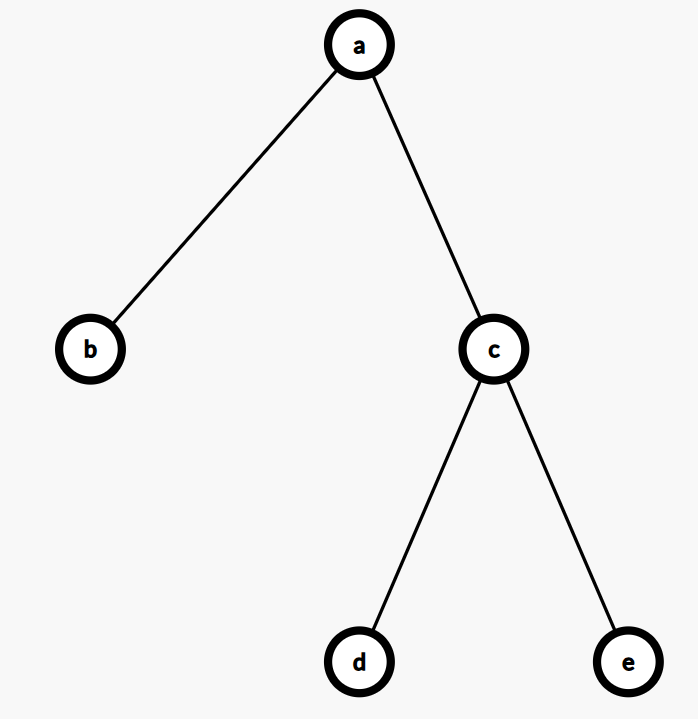
最短颜色序列是 abacdcec，如果没用完某种颜色，可以往同种颜色后面一直添加，例如变成 abacccccdcec。

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;

const int N = 2e5 + 5;
int a[N], cnt[N], n;
vector<pair<int, int>> e[N];

void dfs(int x)
{
    for(auto [i, j] : e[x])
    {
        for(int k = 1; k <= j; k ++) cout << i << " ";
        dfs(i);
        cout << x << " ";
    }
}

void solve()
{
    cin >> n;
    for(int i = 1; i <= n; i ++) cnt[i] = 0, e[i].clear();
    for(int i = 1; i <= n; i ++)
    {
        int x; cin >> x;
        a[i] = x;
        cnt[x] ++;
    }
    set<pair<int, int>> s;
    int fs;
    for(int i = 1; i <= n; i ++)
        if(cnt[i]) s.insert({cnt[i], i}), fs = i;
    int cc = s.size();
    while(s.size() > 1)
    {
        int a = s.begin()->second, b = s.rbegin()->second;
        if(fs == a) fs = b;
        e[b].push_back({a, cnt[a]});
        cc --;
        s.erase({cnt[a], a}); cnt[a] --;
        s.erase({cnt[b], b}); cnt[b] --;
        if(cnt[b]) s.insert({cnt[b], b});
    }
    if(cc != 1)
    {
        sort(a + 1, a + n + 1);
        for(int i = 1; i <= n; i ++) cout << a[i] << " ";
    }
    else if(s.empty())
    {
        dfs(fs);
    }
    else
    {
        for(int i = 0; i < s.begin()->first; i ++) cout << s.begin()->second << " ";
        dfs(s.begin()->second);
    }
    cout << "\n";
}

int main()
{
    ios::sync_with_stdio(false);cin.tie(0);
    int t;cin >> t;while(t --) solve();

    return 0;
}