P5659-树上的数

P5659 [CSP-S2019] 树上的数

直接讲正解。

首先要知道的是，字典序最小意味着：从小到大对每个点贪心选择能到达的最小点。

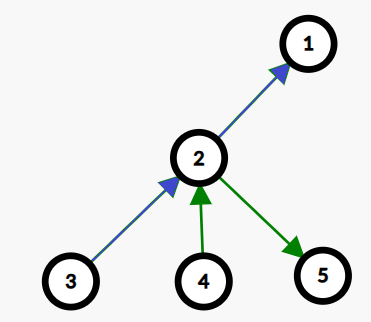
看上图，如果要把 \(3\) 号点通过断边移动到 \(1\) 号点，那么需要依次断 \((3,2),(2,1)\) 边。

但是如果 \(4\) 号点也要移动到 \(5\) 号点呢？这时候就需要决策断边的顺序了。

令 \(i_j\) 表示 \(i\) 号点连的边中第 \(j\) 条断掉的边。

注意到，如果要将一个点从 \(a_0\) 移动到 \(a_{n+1}\)，中间依次经过 \(a_1,a_2,\cdots a_n\)，那么显然需要依次断 \((a_0,a_1),\cdots,(a_n,a_{n+1})\) 这些边。

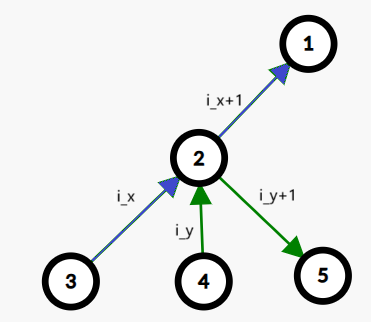
并且：

• 两条边 \((a_{x-1},a_x),(a_x,a_{x+1})\) 在 \(a_x\) 中一定是先后连着断边的。（即 \(\exists j,\text{s.t.}(a_{x-1},a_x)=i_j,(a_x,a_{x+1})=i_{j+1}\)）。
  否则就会出现：把 \((a_{x-1},a_x)\) 断掉之后，中间又断了个 \((k,a_x)\)，那么好不容易从 \(a_0\) 移动到 \(a_x\) 的点就被抢到 \(k\) 去了。。

• \((a_0,a_1)\) 一定是 \(a0_1\)，即 \(a_0\) 第一条断的边。否则还没开始转移呢，\(a_0\) 就被抢走了。

• \((a_n,a_{n+1})\) 一定是 \(an+1_{deg}\)，即 \(a_{n+1}\) 最后一条断的边。否则好不容易转移完，又被后面断的边抢走了。。

注意到这相当于将两条边断边的顺序绑在一起（因为要连着断边），于是考虑使用链表维护。

接下来的图中， \(i_x\) 会向 \(i_{x+1}\) 连一条橙线表示相对顺序已经确定。

特别的，\(first_i\) 连向 \(i_1\)，\(i_{deg}\) 连向 \(end_i\) 。

• 重要：
  • 如果某种中间情况合法，那么一定满足对于任意一个点 \(i\)，从 \(first_i\) 开始，
    • 要么无法到达 \(end_i\)；
    • 要么能够到达，并且一定经过连接该点的所有边。
  • 如果某种结束情况合法，那么一定满足对于任意一个点 \(i\)，从 \(first_i\) 开始，能够到达 \(end_i\)，并且一定经过连接该点的所有边，否则剩下的边就无法确定。

---

手模样例辅助理解。

下位用 \((i)[j]\) 表示值为 \(i\)，编号为 \(j\) 的点。若无特殊说明，默认说的是编号。

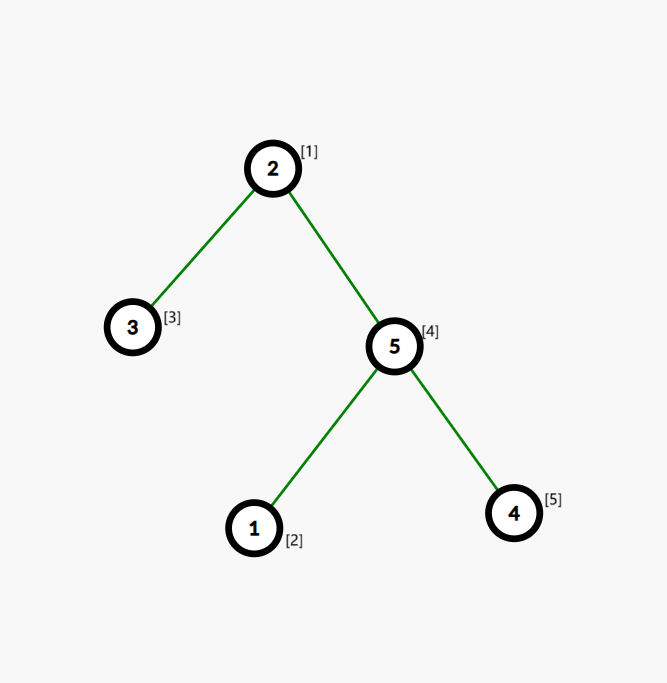
这是样例。

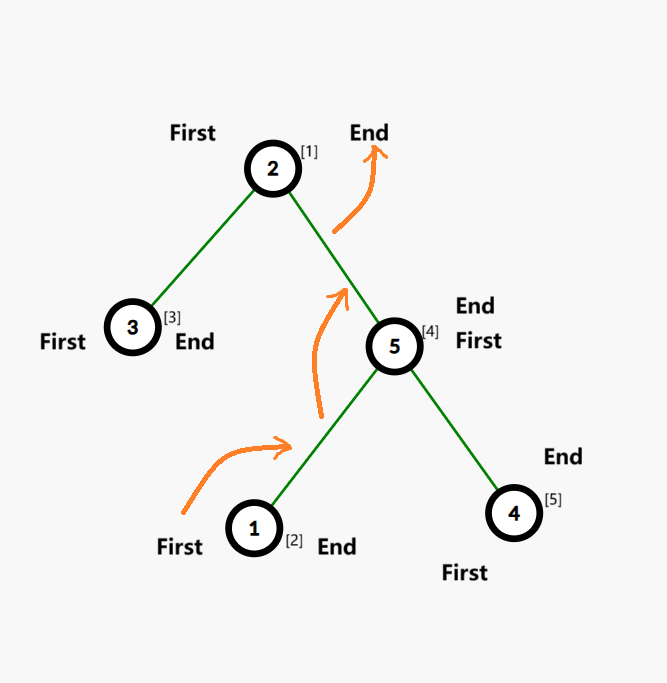
考虑 \((1)[2]\) 号点。

发现值为 \(2\) 的点 \((2)[1]\) 没有被选，选它。此时 \(2\rightarrow 4\rightarrow 1\) 确定了 \(First_2,(2,4)\) 和 \((2,4),(1,4)\) 和 \(End_1,(1,4)\) 的关系（原因：起点要是第一条边，中间的边要严格先后相邻，终点要是最后一条边）。

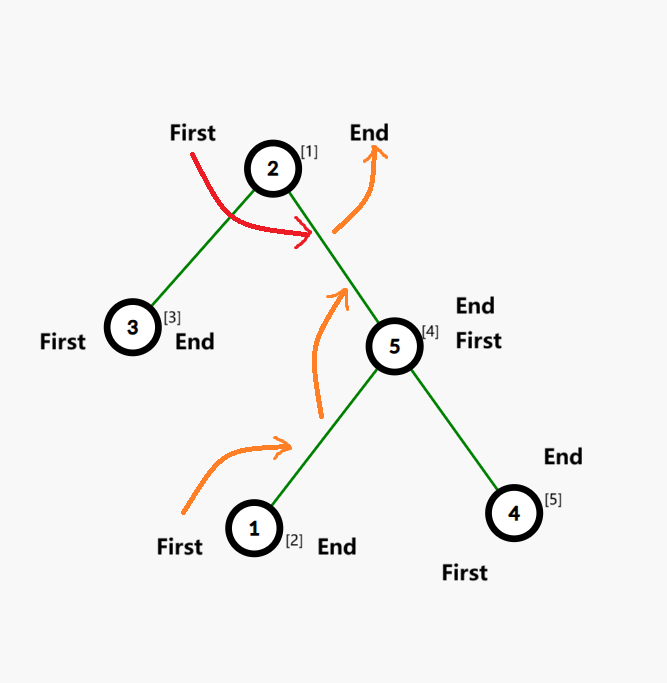
考虑 \((2)[1]\) 号点。

选 \((1)[2]\) 号点（应该是向 \((5)[4]\) 号点方向移动）可以吗？No.因为如果这样，那么 \((1,4)\) 和 \(First_1,End_1\) 同时连边，\((1,3)\) 咋办？

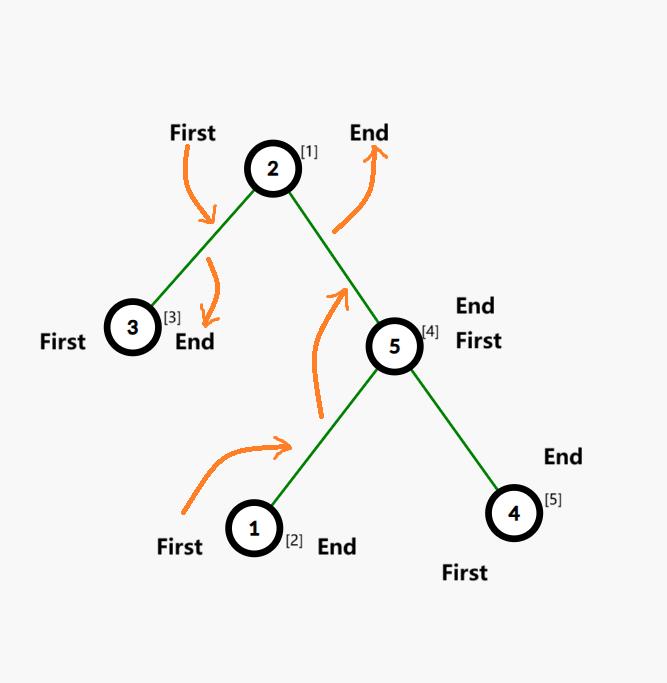
于是考虑 \((3)[3]\) 号点（方向），发现可行。于是确定 \(First_1,(1,3)\) 和 \((1,3),End_3\) 关系。

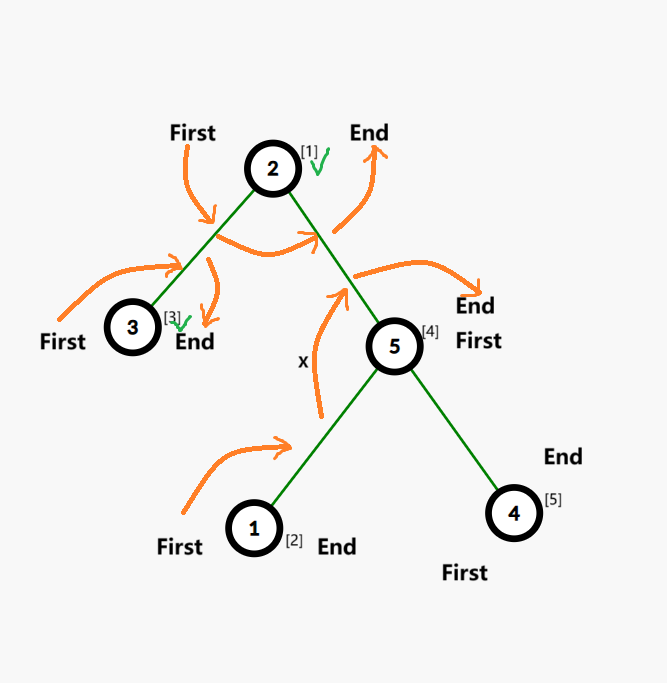
考虑 \((3)[3]\) 号点，\([1]\) 号点被选过，于是考虑 \([2]\) 号点，发现不可行（和已有关系 X 冲突）。于是选 \([4]\) 号点。

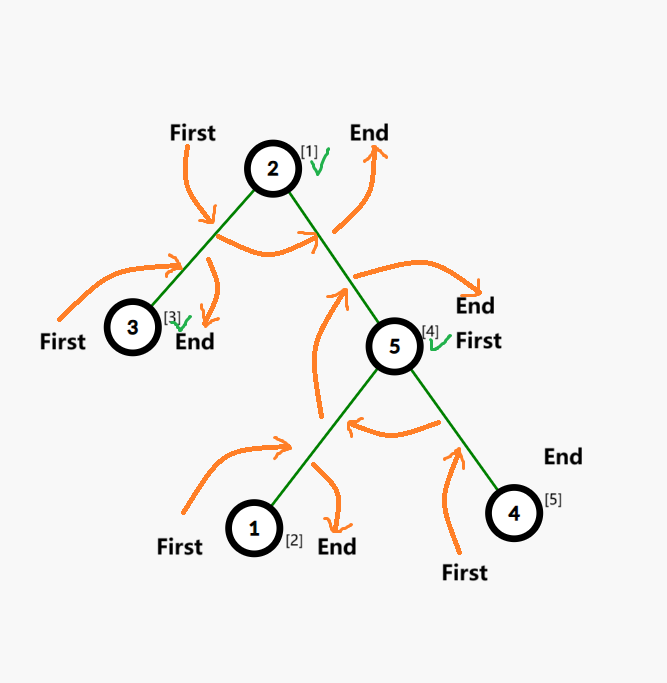
考虑 \((4)[5]\) 号点，\([2]\) 号点可行，于是选择 \([2]\) 号点。

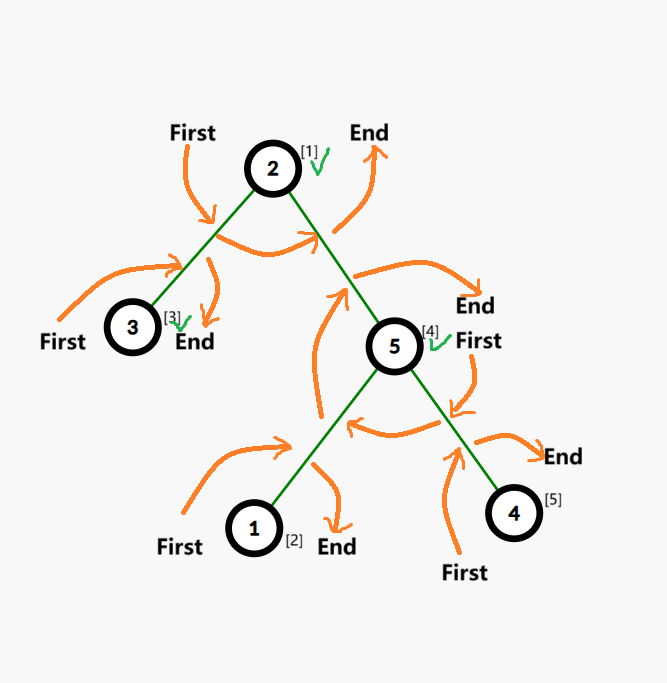
考虑 \((5)[4]\) 号点，只有 \([5]\) 号点，并且可行。

发现，每个点 \(i\) 的连边都是从 \(First_i\) 一直连到 \(End_i\)。

---

细节：

• 链表判断能够连接的时候记得还要用并查集判断：

  • 连完之后会不会提前联通 \(First\rightarrow End\)？
  • 会不会出现自环？（\(i_x\rightarrow i_y\rightarrow \cdots\rightarrow i_x\)）

• 好像是个 \(O(n^3)\) 的？可以一遍 \(dfs\) 判断可行，就成 \(O(n^2)\) 了。

代码：

非常好写，1h写+调，调完小样例一遍过。

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;

const int N = 2005;
struct edge{int v, id;};
vector<edge> e[N];

struct List
{
    List *nxt, *pre;
    int v;
    void clear()
    {
        nxt = pre = NULL;
    }
}ft[N], ed[N], a[N << 1];

int fa[N << 2];

int find(int x) {return x == fa[x] ? x : fa[x] = find(fa[x]);}

inline void merge(int x, int y)
{
    int fx = find(x), fy = find(y);
    fa[fx] = fy;
}

inline void merge(List &l, List &r)
{
    merge(l.v, r.v);
    l.nxt = &r, r.pre = &l;
}

inline bool cmerge(List l, List r)
{
    return l.nxt == NULL && r.pre == NULL && find(l.v) != find(r.v);
}

inline bool chk(List x, List y, List u, List v)
{
    int fx = find(x.v), fy = find(y.v), fu = find(u.v), fv = find(v.v);
    return (fx == fu) && (fy == fv);
}

int n, p[N], deg[N], us[N];

void init()
{
    for(int i = 1; i <= n; i ++) e[i].clear();
    for(int i = 1; i <= n; i ++)
    {
        ft[i].clear(), ed[i].clear();
        ft[i].v = (n << 1) + (i << 1);
        ed[i].v = (n << 1) + (i << 1 | 1);
    }
    for(int i = 1; i <= (n << 1); i ++)
        a[i].clear(), a[i].v = i;
    memset(deg, 0, sizeof deg);
    memset(us, 0, sizeof us);
    for(int i = 1; i <= (n << 2); i ++) fa[i] = i;
}

bool vis[N];

void dfs(int x, int fa, List &fr)
{
    if(cmerge(fr, ed[x]) && !(us[x] < deg[x] - 1 && find(ft[x].v) == find(fr.v)))
        vis[x] = 1;
    for(auto i : e[x])
    {
        if(i.v == fa) continue;
        if(!cmerge(fr, a[i.id]) || (us[x] < deg[x] - 1 && chk(ft[x], ed[x], fr, a[i.id]))) continue;
        dfs(i.v, x, a[i.id ^ 1]);
    }
}

bool add(int x, int u, int fa, List &fr)
{
    if(x == u)
    {
        merge(fr, ed[x]);
        return true;
    }
    for(auto i : e[x])
    {
        if(i.v == fa) continue;
        if(add(i.v, u, x, a[i.id ^ 1]))
        {
            merge(fr, a[i.id]);
            us[i.v] ++;
            return true;
        }
    }
    return false;
}

void solve()
{
    cin >> n;
    init();
    for(int i = 1; i <= n; i ++)
        cin >> p[i], deg[i] = 1;
    for(int i = 1; i < n; i ++)
    {
        int x, y;cin >> x >> y;
        e[x].push_back({y, i << 1});
        e[y].push_back({x, i << 1 | 1});
        deg[x] ++, deg[y] ++;
    }
    for(int i = 1; i <= n; i ++)
    {
        memset(vis, 0, sizeof vis);
        dfs(p[i], 0, ft[p[i]]);
        vis[p[i]] = 0;
        int u = n + 1;
        for(int j = 1; j <= n; j ++)
            if(vis[j])
            {
                u = j;
                break;
            }
        us[p[i]] ++;
        add(p[i], u, 0, ft[p[i]]);
        cout << u << " ";
    }
    cout << "\n";
}

signed main()
{
    ios::sync_with_stdio(0);cin.tie(0);
    int t;cin >> t;while(t --) solve();

    return 0;
}

---

后记

自己想根本不会，看了题解也半懂不懂。。

懂了以后就快了。

花了我一个下午加晚上（\(8h\pm\)）。