[模板][持续更新]欧拉回路与欧拉路径浅析
Luogu P2731 骑马修栅栏 Riding the Fences
题目背景
Farmer John每年有很多栅栏要修理。他总是骑着马穿过每一个栅栏并修复它破损的地方。
题目描述
John是一个与其他农民一样懒的人。他讨厌骑马，因此从来不两次经过一个栅栏。你必须编一个程序，读入栅栏网络的描述，并计算出一条修栅栏的路径，使每个栅栏都恰好被经过一次。John能从任何一个顶点(即两个栅栏的交点)开始骑马，在任意一个顶点结束。
每一个栅栏连接两个顶点，顶点用1到500标号(虽然有的农场并没有500个顶点)。一个顶点上可连接任意多(>=1)个栅栏。两顶点间可能有多个栅栏。所有栅栏都是连通的(也就是你可以从任意一个栅栏到达另外的所有栅栏)。
你的程序必须输出骑马的路径(用路上依次经过的顶点号码表示)。我们如果把输出的路径看成是一个500进制的数，那么当存在多组解的情况下，输出500进制表示法中最小的一个 (也就是输出第一位较小的，如果还有多组解，输出第二位较小的，等等)。
输入数据保证至少有一个解。
输入输出格式
输入格式：
第1行: 一个整数F(1 <= F <= 1024)，表示栅栏的数目
第2到F+1行: 每行两个整数i, j(1 <= i,j <= 500)表示这条栅栏连接i与j号顶点。
输出格式：
输出应当有F+1行，每行一个整数，依次表示路径经过的顶点号。注意数据可能有多组解，但是只有上面题目要求的那一组解是认为正确的。
输入输出样例
9 1 2 2 3 3 4 4 2 4 5 2 5 5 6 5 7 4 6
1 2 3 4 2 5 4 6 5 7
说明
题目翻译来自NOCOW。
USACO Training Section 3.3
Solution:
来系统地整理一下有关欧拉回路和欧拉路径的问题。
什么是欧拉路径？在图上用一种走法经过所有的边一次且只有一次的路径叫做欧拉路径。即一笔画。
如果这条路径的起点和终点重合，那么就是欧拉回路。
如何判断图是否有欧拉回路或者欧拉路径？
无向图：因为欧拉路径中，除了起点与终点以外，任意点的“进”“出”次数相等，所以除了两个点为奇点（度数为奇数的点）（终点和起点）以外，其它点的度数均为偶数。
如果是欧拉回路，奇点的个数应该为0。
有向图：欧拉路径中，最多只有两个点的入度不等于出度。起点出度比入度大1，终点入度比出度大1。
如果是欧拉回路，所有点的 入度=出度 。
寻找欧拉回路或欧拉路径的算法有？
Fluery算法和Hierholzer算法。后者好像也有博客称逐步插入回路法。
后面一种算法无论是编程复杂度还是时间复杂度好像都比前种算法复杂度更优，但前者的应用广泛性好像比后者更高。欧拉回路的更高级的应用还没涉及，如果之后有什么新内容再来补充吧....所以这里就用Hierholzer算法了。
Hierholzer算法自动寻找欧拉回路，在找不到欧拉回路的情况下会找到欧拉路径。前提是得给它指定好起点。
算法流程（无向图）：
1.判断奇点数。奇点数若为0则任意指定起点，奇点数若为2则指定起点为奇点。
2.开始递归函数Hierholzer(x):
循环寻找与x相连的边(x,u):
删除(x,u)
删除(u,x)
Hierholzer(u);
将x插入答案队列之中
3.倒序输出答案队列
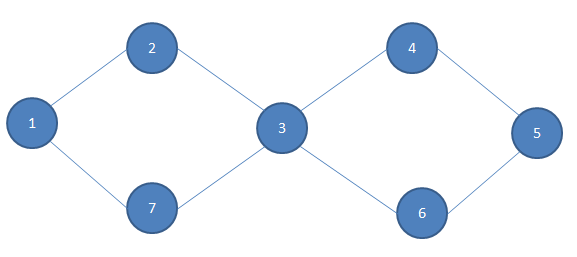
对于该图，算法的执行流程如下：
1.找到该图没有奇点，从1开始进行Hierholzer算法。
2.删边1-2 递归到2
3.删边2-3 递归到3
4.删边3-7 递归到7
5.删边7-1 递归到1
6.1无边，1加入队列，返回
7.7加入队列，返回
8.删边3-4 递归到4
9.删边4-5 递归到5
10.删边5-6 递归到6
11.删边6-3 递归到3
12.3加入队列，返回
13.6加入队列，返回
14.5加入队列，返回
15.4加入队列，返回
16.3加入队列，返回
17.2加入队列，返回
18.1加入队列，返回
答案队列为：1 7 3 6 5 4 3 2 1。反向输出即为答案。
有向图除判断是否存在有一点点不同以外同理。
对于该题【欧拉路径/欧拉回路】模板题，要求输出答案的最小序列。所以起点首先要选的尽量小，然后在边的储存上面加一点小trick。
使用邻接表储存图时，除了用链式前向星还可以用vector储存。我们可以把vector换成multiset，这样就可以保证该点前往的下一个点是最小值，同时保证了答案的最小值。
下面是该题的代码：
#include<bits/stdc++.h> using namespace std; const int N=1025; multiset<int> to[N]; int len[N]; int road[N],k; void dfs(int x){ for(auto a=to[x].begin();a!=to[x].end();a=to[x].begin()){//auto类型为C++11标准，可进行自动类型推断 int u=*a; to[x].erase(a); to[u].erase(to[u].find(x));//删边 dfs(u);//递归 } road[k++]=x;//往答案队列里插入答案 } int main(){ int m,a,b; scanf("%d",&m); for(int i=0;i<m;i++){ scanf("%d%d",&a,&b); len[a]++,len[b]++; to[a].insert(b); to[b].insert(a); } int s=-1,e=-1;//起点与终点 for(int i=1;i<=1024;i++) if(len[i]%2==1){ if(s==-1)s=i; else if(e==-1)e=i; else exit(1); }//判断每个点的度数 if(s==-1)s=1; dfs(s);//开始递归 for(k=k-1;k>=0;k--) printf("%d\n",road[k]);//倒序输出答案 return 0; }
之后会填Fluery算法和欧拉路径更高级应用的坑。（大概）
