51 Nod 1281 山峰和旗子

 

 

 

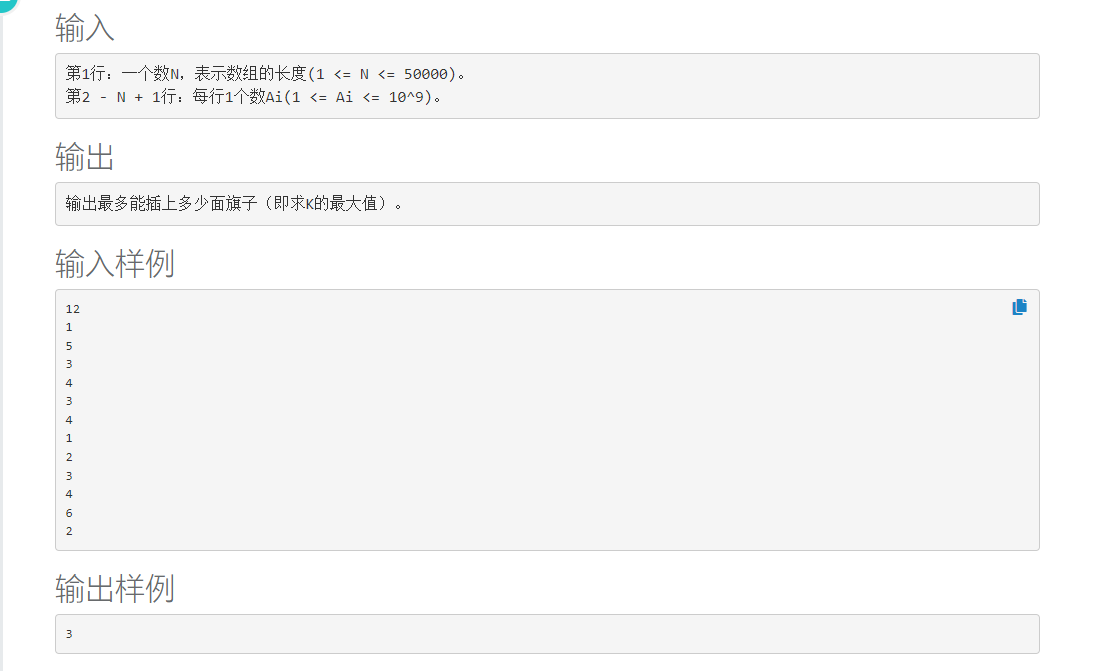
 解题思路:首先先把能当做山峰的点找出来即a[i-1]<a[i]<a[i+1],收入集合中，其次从1开始遍历用二分找到距离大于等于i的，找到i面继续循环，往下循环直至找不到i面

注意：我们不仅要存放旗子的高度且要存储每面旗子初始的距离，所以要用结构体struct E,其次是在二分时循环变量的处理，当找第一个时，去处理第二个由于间距必须>=j，那么    e[2]-e[1]>=j  <=> e[2]>=e[1]+j

即用二分找到大于等于e[1]+j的数，以此类推。

#include <bits/stdc++.h>
using namespace std;
const int N=50010;
int a[N],e[N];
int main() {
    int n;
    cin>>n;
    for(int i=1;i<=n;i++)
    cin>>a[i];
    int k=0;
    for(int i=2;i<n;i++)
    {
        if(a[i]>a[i-1]&&a[i]>a[i+1])
        {
            e[k]=i;
            k++;
            i++;
        }
    } 
    if(k==0)
    {
        cout<<0;
        return 0;
    }
      if(k==1)
       {
            cout<<1<<endl;
            return 0; 
       }
    for(int j=1;j<=k;j++)
    {
       int ans=0;
       for(int i=0;i<k;)
       {
              ans++;
              int t=lower_bound(e,e+k,e[i]+j)-e;
              if(t==k) break;
              else {
                       i=t;
              }
          if(ans==j) break;
       }
       if(ans<j) 
       {
           cout<<j-1;
           break;
       }
    }
    return 0;
}