51Nod 1163 最高的奖励

 

 

 

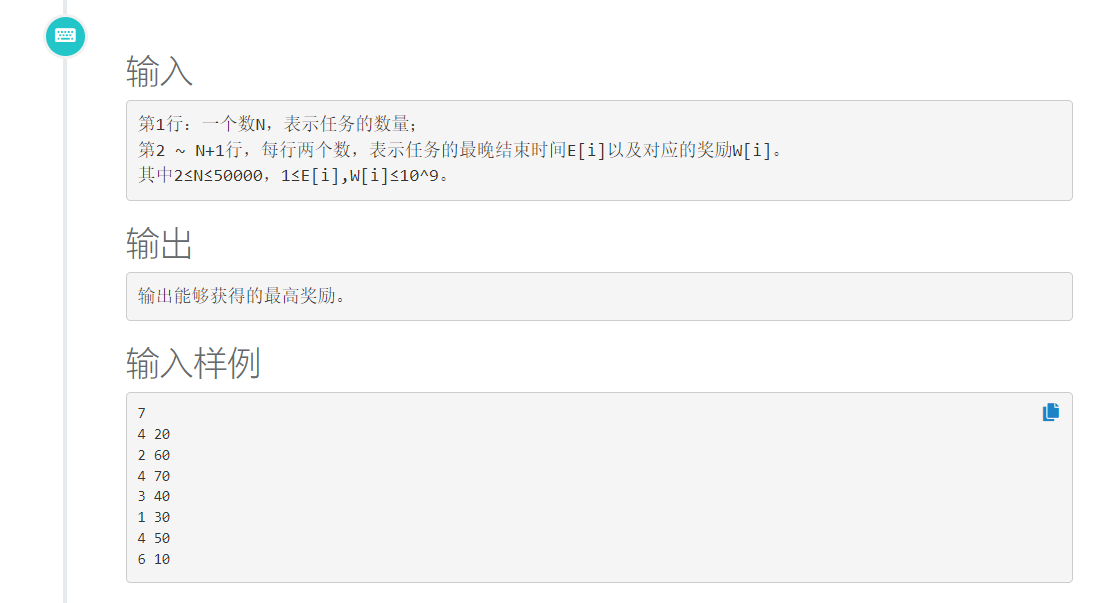
思路：优先队列，以结束时间为关键字进行排序，最好的结果是全部放入队列中，但必然会出现冲突，我们从头开始遍历当冲突出现时即现在的时间放不下这么多的东西，我们需要前面的数腾位置，为了使值最大让最小的出去，此时只能用堆即优先队列，来维护。

特别注意：对取堆顶的判断条件，当结束时间<=堆的大小时，需要堆顶需要出队列，例如结束时间为4，堆的大小为4,此时进队肯定是冲突的，堆的大小为4说明前面1，2，3，4位都排好了，再进来时间不允许必定冲突。当结束时间大于堆的大小时，可以直接入队，因为其结束时间不会对前面已经生成的堆产生影响并且可以增加奖励值。

 

#include<iostream>
#include<algorithm>
#include<queue>
#include<vector>
using namespace std;
const int N=5e4+10;
struct E
{
	int t;
	int v;
}e[N];
bool cmp(E z,E w)
{
	return z.t<w.t;
}
int main()
{
	int n;
	scanf("%d",&n);
	for(int i=1;i<=n;i++)
	{
		int t,v;
		scanf("%d%d",&t,&v);
		e[i]={t,v};
	}
	sort(e+1,e+n+1,cmp);
	priority_queue<int,vector<int>,greater<int>> heap;
	long long res=0;
	for(int i=1;i<=n;i++)
	{
	    unsigned int k=e[i].t;        //取出当前的结束时间再和堆的大小判断
	    if(k<=heap.size())	          //堆的大小代表的是已经排好的选择一个选择占用一个时间 
		{                             //如果当前遍历的时间小于堆的大小那么其就有可能为答案  
		                              //与堆顶比较 
			int tp=heap.top();
			if(tp<e[i].v)
			{
				res-=tp;              //减值 
				heap.pop();           //弹出 
				res+=e[i].v;          //加值 
				heap.push(e[i].v);    //进堆 
			}
		}else 
		{
			res+=e[i].v;
			heap.push(e[i].v);
		 } 
	}
	printf("%lld",res);
	return 0;
 }