DFS——关于洛谷P2802-回家的思考

  题目链接：https://www.luogu.com.cn/problem/P2802

  解题主要思路：1.通过理解题意和观察到题目的变量范围：1<=n,m<=9，便可推断出本题大致要用DFS。

  AC代码展示：   

  ——note:题意简简单单，但实际写起来注意事项还蛮多的。 

#include<bits/stdc++.h>
using namespace std;
int n,m;
int s[100][100];
//int book[100][100];  book数组不用开  因为题目没有说不能走重复的路径
int sx,sy;
int dis[4][2]={{-1,0},{0,1},{1,0},{0,-1}};
int hp1=6;
int minn=999999;  //原则上minn设置成比m*n大一点的数
void dfs(int t,int x,int y,int hp){
    if(t>=minn){   //剪枝策略   减去不用的循环
        return;
    }
    if(s[x][y]==3){  //终点判断
        minn=min(minn,t);
        return;
    }
    if(t>=(n*m/2)){  //剪枝策略  不然会在两个鼠标处来回逛 无限循环
        return;
    }
    if(s[x][y]==4){  //捡起鼠标
        hp=6;
    }
    if(hp==1){  //剪枝策略  
        return;
    }
    for(int i=0;i<4;i++){
        int x1=x+dis[i][0];
        int y1=y+dis[i][1];
        if((x1>=0&&x1<n)&&(y1>=0&&y1<m)&&s[x1][y1]!=0&&s[x1][y1]!=2){//别回到终点  别撞到墙上
            dfs(t+1,x1,y1,hp-1);  //hp 和 t不建议设成常量  因为这两个量是随着枚举状态变化而变化  设成常量会出错
        }
    }
}
int main(){
    scanf("%d%d",&n,&m);
    for(int i=0;i<n;i++){
        for(int j=0;j<m;j++){
            scanf("%d",&s[i][j]);
            if(s[i][j]==2){
                sx=i;
                sy=j;
            }
        }
    }
    dfs(0,sx,sy,6);
    if(minn==999999){//  不能设置成0  要设置成原来的量  因为可以这么理解  没到终点的话就不会改变minn
        cout<<-1;
    }else{
        cout<<minn;
    }
}

  注意事项：1.题目上并没有说不可以走重复的路径，而且从题意也可以推测出有些案例必须要走重复的路径，所以标记数组即book数组就可以不用开了，这就要注意别让程序无限递归！,就是在两个鼠标之间无                      限走来走去

                    2.为了解决无限递归的问题，这就要设置dfs函数的参量step(步数)的上限了，一般按经验是取到n*m/2为最大值。

                    3.判断是否捡到鼠标的放置也要有讲究，要位于“处理区”，而且是在位于特定位置上,必须要判断hp==1前面。

                    

 

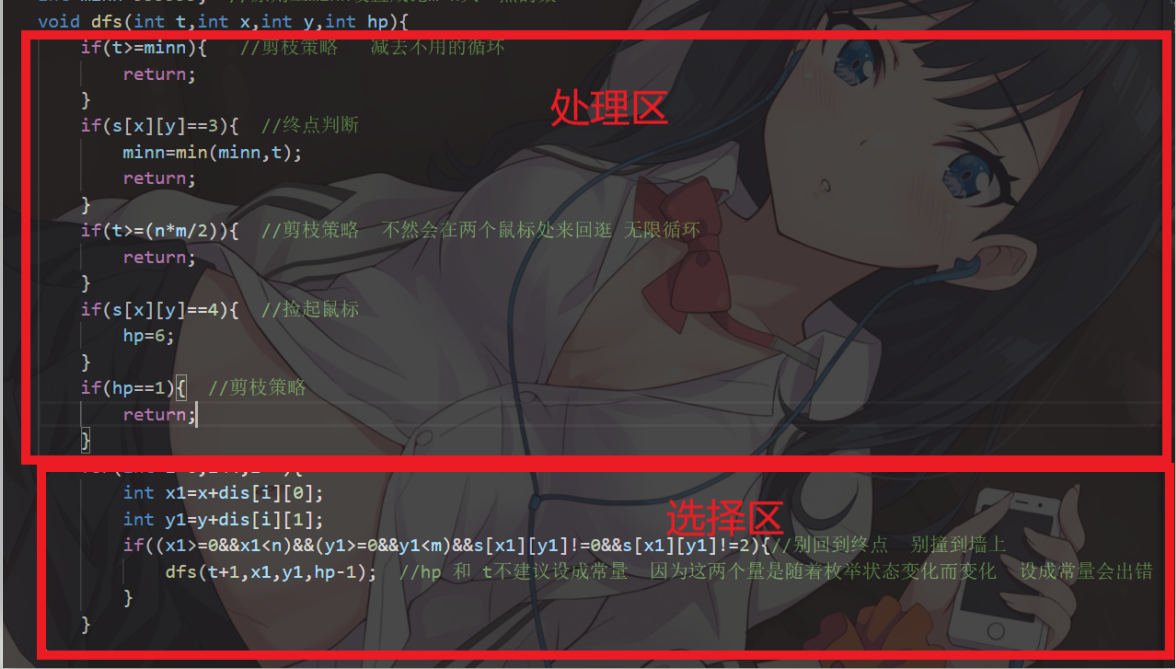
                    4.我一开始写本程序的时候就想让hp(生命值)设置成全程变量，但这样写会wa，因为hp是随着枚举的状态的变化而变化,所以更好的选择是放在函数的形参当中，t(步数也类似)。

                    5.minn等于原值时才是没有路径可以回家，可以这么理解，因为没有路径可以回家，也就是无法更新minn，所以minn为初值，反过来也一样，故是一个充要条件。

                    6.即使注意到了以上几点，还是会超时tle，必须要在开头加个判断if，即如果t>=minn，就放弃它，避免做无用功，这是一个简单的剪枝。