洛谷 P1351 联合权值 题解

P1351 联合权值

题目描述

无向连通图 \(G\) 有 \(n\) 个点，\(n-1\) 条边。点从 \(1\) 到 \(n\) 依次编号,编号为 \(i\) 的点的权值为 \(W_i\)​，每条边的长度均为 \(1\)。图上两点 \((u, v)\) 的距离定义为 \(u\) 点到 \(v\) 点的最短距离。对于图 \(G\) 上的点对 \((u, v)\)，若它们的距离为 \(2\)，则它们之间会产生\(W_v \times W_u\)​ 的联合权值。

请问图 \(G\) 上所有可产生联合权值的有序点对中，联合权值最大的是多少？所有联合权值之和是多少？

输入格式

第一行包含 \(1\) 个整数 \(n\)。

接下来 \(n-1\) 行,每行包含 \(2\) 个用空格隔开的正整数 \(u,v\)，表示编号为 \(u\) 和编号为 \(v\) 的点之间有边相连。

最后 \(1\) 行,包含 \(n\) 个正整数，每两个正整数之间用一个空格隔开，其中第 \(i\) 个整数表示图 \(G\) 上编号为 \(i\) 的点的权值为 \(W_i\)​。

输出格式

输出共 \(1\) 行,包含 \(2\) 个整数，之间用一个空格隔开,依次为图 \(G\) 上联合权值的最大值和所有联合权值之和。由于所有联合权值之和可能很大，输出它时要对\(10007\)取余。

输入输出样例

输入 #1

5
1 2
2 3
3 4
4 5
1 5 2 3 10

输出 #1

20 74

说明/提示

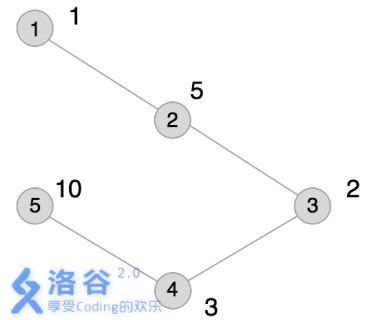
本例输入的图如上所示，距离为2 的有序点对有\(( 1,3)\) 、\(( 2,4)\) 、\(( 3,1)\) 、\(( 3,5)\)、\(( 4,2)\) 、\(( 5,3)\)。

其联合权值分别为2 、15、2 、20、15、20。其中最大的是20，总和为74。

【数据说明】

对于30%的数据，\(1 < n \leq 100\)；

对于60%的数据，\(1 < n \leq 2000\)；

对于100%的数据，\(1 < n \leq 200000, 0 < W_i \leq 10000\)。

保证一定存在可产生联合权值的有序点对。

【思路】

树上问题 + dfs
一开始没往树上操作这个地方想就想打个暴力搜索那点部分分
然后发现暴搜是很麻烦的，好像是没法处理类似菊花图的图形
所以只能上树
可以分为两个部分第一个部分先预处理出每一个点对应的长度为1的菊花图里面的最大值和最大值的位置，同时也求出
这个点对应的菊花图里面所有子节点的和
因为后面求总和的时候可以用一个点的值乘以这个菊花图的总和减去那个点的值
然后再来一个dfs
先处理处不是菊花图也就是直上直下不拐弯的那种可能出现的情况也暴力比较找最大值
然后再枚举菊花图，比较里面哪一个除了最大点的点和最大的的乘积最大
也就是找出次大点记录，同时求和，就用上面的方法就可以了

【完整代码】

#include<iostream>
#include<cstdio>
#include<vector>

using namespace std;
const int Max = 2e5 + 10;
const int mo = 1e4 + 7;
int a[Max];
int father[Max];
int maxw[Max],maxv[Max];//某个点对应的子节点里面的最大值和最大值的位置 
int sum[Max];//某个点对应的子节点之和 
vector<int>e[Max];
int n;
int ans1,ans2;

void dfs1(int x,int fa)
{
	for(int i = 0;i < e[x].size();i ++)
	{
		if(e[x][i] != fa)
		{
			if(a[e[x][i]] > maxw[x])
				maxw[x] = a[e[x][i]],maxv[x] = e[x][i];
			sum[x] = (sum[x] + a[e[x][i]]) % mo;
			dfs1(e[x][i],x); 
		}
	}
}

void dfs2(int x,int fa)
{
	father[x] = fa;
	if(father[father[x]] != 0)
	{
		ans1 = max(ans1,a[father[father[x]]] * a[x]);
		ans2 = (ans2 + 2 * a[x] * a[father[father[x]]]) % mo;
	}
	for(int i = 0;i < e[x].size();i ++)
	{
		if(e[x][i] != fa)
		{
			if(e[x][i] != maxv[x])ans1 = max(ans1,a[e[x][i]] * maxw[x]);
			ans2 = (ans2 + a[e[x][i]] * (sum[x] - a[e[x][i]])) % mo;
			dfs2(e[x][i],x);
		}
	}
}

int main()
{
//	freopen("2","r",stdin); 
	int x,y;
	scanf("%d",&n);
//	for(int i = 1;i <= n;++ i)
//		father[i] = i;
	for(int i = 1;i < n;++ i)
	{
		scanf("%d%d",&x,&y);
		e[x].push_back(y);
		e[y].push_back(x);
	}
	for(int i = 1;i <= n;++ i)
		scanf("%d",&a[i]);
	dfs1(1,0);
	dfs2(1,0);
	cout<<ans1<<" "<<ans2 % mo<<endl;
	return 0;
}