最短路问题算法总结

BFS

#include <iostream>
#include <cstring>
#include <queue>

using namespace std;
const int N = 1e5 + 10;

int n, m, h[N], e[N], idx, ne[N], d[N];
queue<int> q;

void add(int a, int b){ //邻接表
    e[idx] = b, ne[idx] = h[a], h[a] = idx ++;
}

int bfs()
{
    q.push(1);
    memset(d, -1, sizeof d);
    d[1] = 0;
    while (!q.empty())
    {
        int t = q.front();
        q.pop();
        for (int i = h[t];i != -1;i = ne[i]) //遍历t的所有子节点
        {
            int j = e[i];
            if (d[j] == -1)
            {
                d[j] = d[t] + 1; //走到j节点，距离 +1
                q.push(j); //压入j节点作为下一次的父节点
            }
        }
    }
    
    return d[n];
}

int main()
{
    memset(h, -1, sizeof h);
    
    cin >> n >> m;
    for (int i = 0;i < m;i ++)
    {
        int a, b;
        cin >> a >> b;
        add(a, b); //有向图
    }
    
    cout << bfs() << endl;
}

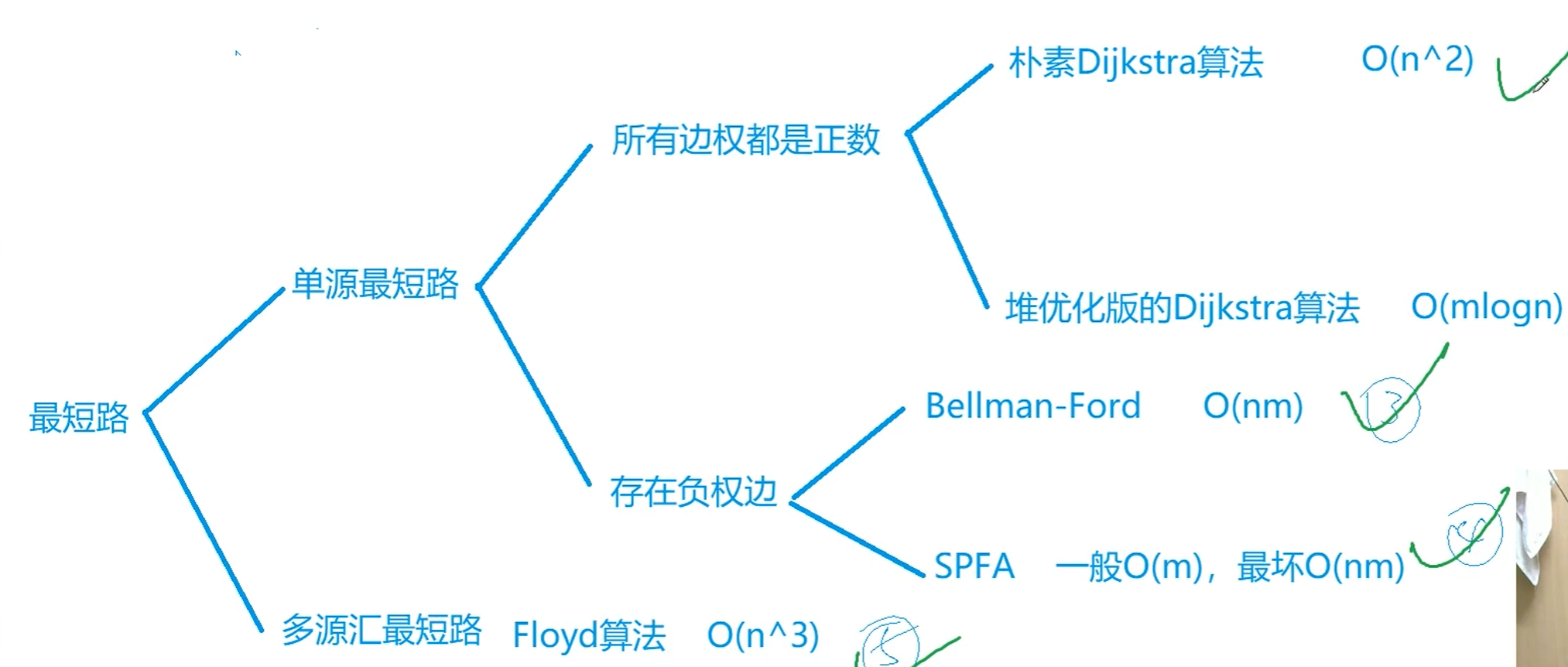
朴素dijkstra

//朴素Dijkstra 邻接矩阵存储稠密图 O(n^2)
#include <bits/stdc++.h>

using namespace std;

const int N = 510;

int n, m,
g[N][N], //g[a][b]:a->b的权重 
dis[N]; //dist[i]:起点到i的距离
bool vis[N]; //st[i]:i点是否已确定最短路

int dijkstra()
{
    memset(dis, 0x3f, sizeof dis); //距离初始化为最大值
    dis[1] = 0; //自身为零
    
    for (int i = 0;i < n;i ++)
    {
        int t = -1; //t是距离最近的未确定最短路点的编号 
        for (int j = 1;j <= n;j ++) //寻找最近的点
            if (!vis[j] && (t == -1 || dis[t] > dis[j]))
                t = j;
                
        if (t == n) break;        
        vis[t] = true;
        
        for (int j = 1;j <= n;j ++ ) //遍历n个点 用最新的点更新迭代所有出边 
            dis[j] = min(dis[j], dis[t] + g[t][j]); 
    }
    
    if (dis[n] == 0x3f3f3f3f) return -1; //无法到达
    return dis[n]; //返回最短距离
}

int main()
{
    cin >> n >> m;
    memset(g, 0x3f, sizeof g);
    
    while (m --)
    {
        int a, b, c;
        cin >> a >> b >> c;
        g[a][b] = min(g[a][b], c); //（有重边）存下最短边长
    }
    
    int t = dijkstra();
    
    printf("%d\n", t);
    
    return 0;
}

堆优化dijkstra

#include <bits/stdc++.h>
#define endl '\n'
#define int long long

using namespace std;

typedef pair<int, int> PII;

const int N = 1e6  + 10, INF = 0x3f3f3f3f3f3f3f3f;
int n, m;
int h[N], e[N], ne[N], idx;
int w[N], d[N];
bool vis[N];

void add(int a , int b, int c){
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++;
}

int dijkstra()
{
    memset(d, INF, sizeof d);
    d[1] = 0;
    priority_queue<PII, vector<PII>, greater<PII>> heap; //小根堆

    heap.push({0, 1}); // 第一个是距离，第二个是编号
    
    while (heap.size())
    {
        auto t = heap.top();
        heap.pop();

        int dis = t.first, ver = t.second;
        
        if (vis[ver]) continue;
        vis[ver] = true;

        for (int i = h[ver];i != -1;i = ne[i])
        {
            int j = e[i];
            if (d[j] > dis + w[i])
            {
                d[j] = dis + w[i];
                heap.push({d[j], j});
            }
        }
    }

    if (d[n] == INF) return -1;
    else return d[n];
}

signed main()
{
    ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);

    cin >> n >> m;
    
    memset(h, -1, sizeof h);
    
    while (m --)
    {
        int a, b, c;
        cin >> a >> b >> c;
        add(a, b, c);
    }

    cout << dijkstra() << endl;

    return 0;
}

SPFA

#include <iostream>
#include <cstring>
#include <queue>
#define endl '\n'

using namespace std;
const int N = 1e5 + 10;
int e[N], h[N], ne[N];
int d[N], w[N], idx, n, m;
bool st[N];

void add(int a, int b, int c){
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++;
}

int spfa()
{
    memset(d, 0x3f, sizeof d);
    d[1] = 0;
    
    queue<int> q;
    st[1] = true;
    q.push(1);
    
    while (!q.empty())
    {
        int t = q.front();
        q.pop();
        
        st[t] = false;
        
        for (int i = h[t];i != -1;i = ne[i])
        {
            int j = e[i];
            if (d[j] > d[t] + w[i])
            {
                d[j] = d[t] + w[i];
                if (!st[j])
                {
                    q.push(j);
                    st[j] = true;
                }
            }
        
        }
    }
    
    return d[n];  
}


int main()
{
    ios::sync_with_stdio(false), cin.tie(0);
    
    memset(h, -1, sizeof h);
    
    cin >> n >> m;
    for (int i = 0;i < m;i ++)
    {
        int a, b, c;
        cin >> a >> b >> c;
        add(a, b, c);
    }
    
    int t = spfa();
    
    if (t == 0x3f3f3f3f ) puts("impossible");
    else cout << t << endl;
    
    return 0;
}

Floyd

#include <iostream>

using namespace std;

const int INF = 1e9;

int d[210][210];
int n, m, k;

void floyd()
{
    for (int k = 1;k <= n;k ++)
    {
        for (int i = 1;i <= n;i ++)
        {
            for (int j = 1;j <= n;j ++)
            {
                d[i][j] = min(d[i][j], d[i][k] + d[k][j]);
            }
        }
    }
}

int main()
{
    cin >> n >> m >> k;
    
    for (int i = 1;i <= n;i ++)
    {
        for (int j = 1;j <= n;j ++)
        {
            if (i == j) d[i][j] = 0;
            else d[i][j] = INF;
        }
    }
    
    
    while (m --)
    {
        int x, y, z;
        cin >> x >> y >> z;
        
        d[x][y] = min(d[x][y], z);
    }
    
    floyd();

    
    while (k --)
    {
        int a, b;
        cin >> a >> b;
        if (d[a][b] >= INF / 4) puts("impossible");
        else cout << d[a][b] << endl;
    }
}