题解【bzoj1010 [HNOI2008]玩具装箱TOY】
斜率优化动态规划可以用来解决这道题。同时这也是一道经典的斜率优化基础题。
分析：明显是动态规划。令\(dp[i]\)为前\(i\)个装箱的最小花费。
转移方程如下：
\[dp[i]=\min\limits_{0 \leq j < i} \{ dp[j]+( \sum \limits_{k = j + 1}^{i}{C_k} + i - j - 1 - L) ^ 2\}
\]
用\(sum[i]\)表示前\(i\)个容器的长度之和（即\(C\)的前缀和），方程简化为：
\[dp[i]=\min\limits_{0 \leq j < i} \{ dp[j]+( sum[i]-sum[j] + i - j - 1 - L) ^ 2\}
\]
又令\(f[i]\)为\(sum[i]+i\)，继续简化方程为：
\[dp[i]=\min\limits_{0 \leq j < i} \{ dp[j]+( f[i]-f[j] - 1 - L) ^ 2\}
\]
暴力dp是\(O(n^2)\)，考虑优化。如何优化，就是用前面所提到的斜率优化。这玩意到底是什么？我们先来继续对状态转移方程进行进一步的推导。
对于每个\(dp[i]\)可以知道都是由一个\(j0\)推过来的。这个\(j0\)对于当前的\(i\)是最优的决策。假设现在有两个决策\(j_1,j_2 (1 \leq j_1 < j_2 < i)\)，且决策\(j_2\)优于\(j_1\)，则有：
\[dp[j_1]+( f[i]-f[j_1] - 1 - L) ^ 2 \geq dp[j_2]+( f[i]-f[j_2] - 1 - L) ^ 2
\]
拆开可得：
\[dp[j_1]+f[i]^2-2f[i](f[j_1]+1+L)+(f[j_1]+L+1)^2 \geq dp[j_2]+f[i]^2-2f[i](f[j_2]+1+L)+(f[j_2]+L+1)^2
\]
化简可得：
\[2f[i](f[j_2] + 1 + L)-2f[i](f[j_1] + 1 + L) \geq dp[j_2]+(f[j_2]+1+L)^2 - (dp[j_1]+(f[j_1]+1+L)^2)
\]
即：
\[2f[i] \geq \frac{dp[j_2]+(f[j_2]+1+L)^2 - (dp[j_1]+(f[j_1]+1+L)^2)}{f[j_2]-f[j_1]}
\]
令\(g[i] = (f[i]+L+1)^2\)，可得：
\[2f[i] \geq \frac{dp[j_2]+g[j_2] - (dp[j_1]+g[j_1])}{f[j_2]-f[j_1]}
\]
也就是说，若\(j1,j2\)满足上面这个式子，那么\(j2\)一定比\(j1\)优。
为什么叫斜率优化？因为上面这个式子可以把看作\(dp[i]+g[i]\)看做纵坐标，\(f[i]\)看做横坐标，上面的等式右侧就相当于\(\frac{\Delta y}{\Delta x}=k\)也就是一个一次函数的斜率。当这个斜率\(k \leq 2f[i]\)则\(j_2\)优于\(j_1\)。
假如我们有三个决策\(j_1,j_2,j_3\)（如下图）
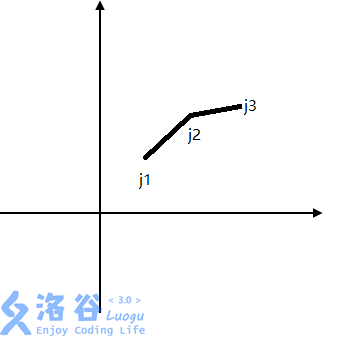
容易证明：\(j_2\)不可能是最优的。
这样一来，每两个决策间的斜率便是单调上升的。
所以有两种做法：
- 对于\(dp[i]\)，有了斜率单调上升这个条件，就可以去二分最优的决策点（也就是斜率小于\(2f[i]\)的）。复杂度\(O(n \log n)\)。
- 又因为\(f[i]\)是单调递增的，可以用单调队列来维护。具体实现就是，把决策放进一个单调队列里，如果队首和当前的\(i\)间的斜率 \(<f[i]\)，就把队首删掉（即h++）。对于队尾，就每次把加入\(i\)后不满足斜率单调上升的队尾全部删掉（即t--），最后把\(i\)放进单调队列就好了。
注意事项：
long long.
还有 $g[0]=(L + 1) ^ 2 $而不是\(0\)!!!!（因为这个我调了很久）
给一下单调队列做法的代码：
#include <iostream>
#include <cstdlib>
#include <cstdio>
#include <algorithm>
using namespace std;
#define int long long
const int MAXN = 50050;
int N, L, dp[MAXN], sum[MAXN], f[MAXN], g[MAXN], h, t, Q[MAXN];
inline double xie(int j1, int j2)
{
return (double) (dp[j2] + g[j2] - dp[j1] - g[j1]) / (f[j2] - f[j1]);
}
#undef int
int main()
{
scanf("%d%d", &N, &L);
for(int i = 1; i <= N; i++)
{
scanf("%d", &sum[i]);
sum[i] += sum[i - 1];
f[i] = sum[i] + i;
g[i] = (f[i] + L + 1) * (f[i] + L + 1);
}
g[0] = (L + 1) * (L + 1); //important!!!
for(int i = 1; i <= N; i++)
{
while(h < t && xie(Q[h], Q[h + 1]) <= 2 * f[i]) h++;
dp[i] = dp[Q[h]] + (f[i] - f[Q[h]] - L - 1) * (f[i] - f[Q[h]] - L - 1); //更新dp值
while(h < t && xie(Q[t], i) < xie(Q[t - 1], Q[t])) t--;
Q[++t] = i;
}
printf("%lld\n", dp[N]);
return 1；//防抄
}
