数学初步
借鉴了多个网址与书
很多都没有给出证明
质数
整除&约数
若\(a\)为\(b\)的因数,则认为a可以整除b,\(a\)为\(b\)的约数 记作: \(a|b\)
\(eg: 2|4 , 3|6 , 8|24\)
互质
若\(a\)与\(b\)没有除了1以外的相同因子,则称a与b互质
质数
若一个数与除了1与自身以外没有任何因数,则称其为质数
推论:质数与除了自身与0以外任何自然数互质
质数的判定:试除法
暴力做法自然可以枚举从小到大的每个数看是否能整除。
bool isPrime(int a) {
if (a < 2) return false;
for (int i = 2; i < a; ++i)
if (a % i == 0) return false;
return true;
}
这样做是十分稳妥了,但是真的有必要每个数都去判断吗?
很容易发现这样一个事实:如果\(x\)为\(a\)的约数,则\(\frac{a}{x}\)也为\(a\)的约数。
这个结论告诉我们,对于每一对\((x, \frac{a}{x} )\),只检验其中的一个就足够了。为了方便起见,我们只考察每一对的较小数。不难发现,所有这些较小数都在 [1, \(\sqrt{a}\)] 这个区间里。
bool isPrime(int a) {
if (a < 2) return 0;
for (int i = 2; (long long)i * i <= a; ++i) // 防溢出
if (a % i == 0) return 0;
return 1;
}
质数筛
如果我们想要知道小于等于 \(n\) 有多少个素数呢?
一个自然的想法是对于小于等于 \(n\) 的每个数进行一次质数检验,这种暴力的做法显然不能达到最优复杂度。于是,我们便需要质数筛法。
Eratosthenes 筛法
考虑这样一件事情:对于任意一个大于 1 的正整数 \(n\),那么它的 \(x\) 倍就是合数\((x > 1)\)。利用这个结论,我们可以避免很多次不必要的检测。
如果我们从小到大考虑每个数,然后同时把当前这个数的所有(比自己大的)倍数记为合数,那么运行结束的时候没有被标记的数就是素数了。
vector<int> prime;
bool is_prime[N];
void Eratosthenes(int n) {
is_prime[0] = is_prime[1] = false;
for (int i = 2; i <= n; ++i) is_prime[i] = true;
for (int i = 2; i <= n; ++i) {
if (is_prime[i]) {
prime.push_back(i);
if ((long long)i * i > n) continue;
for (int j = i * i; j <= n; j += i)
// 因为从 2 到 i - 1 的倍数我们之前筛过了,这里直接从 i
// 的倍数开始,提高了运行速度
is_prime[j] = false; // 是 i 的倍数的均不是素数
}
}
}
复杂度:\(O(\sum\limits_{质数p}^{N}\frac{N}{p})=O(N log log N)\)
线性筛法
埃氏筛法仍有优化空间,它会将一个合数重复多次标记。有没有什么办法省掉无意义的步骤呢?答案是肯定的。
如果能让每个合数都只被标记一次,那么时间复杂度就可以降到 \(O(n)\) 了。
可以通过从大到小累计质因子的方式筛除一个数。
int v[maxn], prime[maxn], m;
void primes(int n) {
for (int i = 2; i <= n; i++) prime[i] = i; //初始化
for (int i = 2; i <= n; i++) {
if (v[i] == 0) { v[i] = i; prime[++m] = i; } //i没有被筛过
//给i乘上质因子
for (int j = 1; j <= m; j++) {
if (prime[j]*i > n) break; //超出范围
if (prime[j] > v[i]) break; //有更小质因子,退出防止重复筛
v[i*prime[j]] = prime[j];
}
}
for (int i = 1; i <= m; i++) cout << prime[i] << endl;
}
约数
质因数分解
算数基本定理
任何一个大于\(1\)的自然数 \(N\),如果\(N\)不为质数,那么\(N\)可以唯一分解成有限个质数的乘积。
试除法分解质因数
void divide(int n) {
m = 0;
for (int i = 2; i*i <= n; i++) {
if (n % i == 0) {
p[++m] = i, c[m] = 0;
while (n % i == 0) n /= i, c[m]++;
}
}
if (n > 1)
p[++m] = n, c[m] = 1;
}
倍数法
类似质数筛
vector<int> factor[500010];
for (int i = 1; i <= n; i++)
for (int j = 1; j*i <= n; j++)
factor[i*j].push_back(i);
最大公约数
我们用\(gcd(a,b)\)表示\(a\)与\(b\)的最大公约数
九章算术:更相减损术
时间复杂度:\(0(n)\)
欧几里得算法
由于\(a\bmod{b}\)可以看成\(a-kb (a\geq kb)\)
则可以将\(gcd(b,a\bmod{b})\)看成k次\(gcd(b,a-b)\)
时间复杂度:O(log
N)
可以使用递归进行求解
int gcd(int a, int b) {
return b ? gcd(b, a % b) : a;
}
最小公倍数
我们用\(lcm(a,b)\)表示\(a\)与\(b\)的最小公倍数
欧拉函数
互质
若\(gcd(a,b) = 1\),则a与b互质
定义
欧拉函数,即 \(\varphi(n)\),表示的是小于等于 \(n\) 和 \(n\) 互质的数的个数。
比如说 \(\varphi(1) = 1\)。
当$ n $ 是质数的时候,显然有 \(\varphi(n) = n - 1\)。
性质
若\(gcd(a,b)=1\),则:
求值
根据算数基本定理,
int phi(int n) {
int m = (sqrt(n+0.5)), ans = n;
for (int i = 2; i <= m; i++) if (n%i == 0) {
ans = ans/i*(i-1);
while ( n%i == 0 ) n /= i;
}
if(n>1) ans = ans/n*(n-1);
return ans;
}
证明
设\(p\)与\(q\)为\(n\)质因子,则 \(1\) ~ \(n\)中\(p\)倍数有\(2p,3p,4p...(n/p)*p\),\(q\)倍数有\(2q,3q,4q...(n/q)*q\)
若要将这\(n/p\)与\(n/q\)除去后,根据容斥原理,应剩余 \(N-\frac{N}{p}-\frac{N}{q}+\frac{N}{pq}=N(1-1/p)(1-1/q)\)
同样的,设\(N\)有\(m\)个质数,分别为\(p_1,p_2...p_m\),则去除这\(n\)个倍数后剩余数字的个数为(其实就是\(\varphi{(n)}\)):
化简后可得:
同余
\(a \equiv b \pmod{m}\) 表示\(a\bmod{m}=b\bmod{m}\)
同余类
对于\(\forall a \in [0,m-1]\),集合\(\{a +km\}(k \in \mathbb{Z})\)中任意数模m都为a,则称该集合为一个模m的同余类,记作
\(\bar{a}\)
剩余系
模\(m\)的剩余系有\(m-1\)个分别为\(\bar{1}、\bar{2}、\bar{3}...\overline{\text{m-1}}\)。它们一起构成了完全剩余系。
\(1\)~\(m\)中与\(m\)互质的数代表的同余类有\(\varphi(m)\)个,他们构成了\(m\)的简化剩余系
\(eg:10的简化剩余系为: \{\bar{1},\bar{3},\bar{7},\bar{9}\}\)
性质
简化剩余系关于模 \(m\) 乘法封闭
费马小定理
若\(p\)为质数,则对于任意整数\(a\),有:
欧拉定理
若\(gcd(a,n)=1\),则
推论
若\(gcd(a,n)=1\),对于任意正整数\(b\),
证明
扩展欧几里得算法(exgcd)
\(B\acute{e}zout\)定理
对于任意整数\(a,b\),必然存在一组\((x,y)\),使得:\(ax+by=gcd(a,b)\)
\(B\acute{e}zout\)给出了解决方法,又被称为扩展欧几里得算法
在欧几里得算法的最后一步,当 \(b=0\) ,显然有 \(x=1,y=0\)使得 \(a*x+b*y=gcd(a,b)\) 成立。
当 \(b>0\) 时,
递归求解即可,边界为\(b=0\)时,此时\(x=1, y=0\)
int ex_gcd(int a, int b, int& x, int& y) {
if (b == 0) {
x = 1;
y = 0;
return a;
}
int d = ex_gcd(b, a % b, x, y);
int temp = x;
x = y;
y = temp - a / b * y;
return d;
}
乘法逆元
如果一个线性同余方程 \(ax \equiv 1 \pmod b\),则 \(x\) 称为 \(a \bmod b\) 的逆元,记作$ a^{-1}$。
费马小定理求逆元
因为 \(ax \equiv 1 \pmod b\)
所以 \(ax \equiv a^{b-1} \pmod b\)
所以 \(x \equiv a^{b-2} \pmod b\)。
然后我们就可以用快速幂来求了。
线性同余方程
形如
的方程称为 线性同余方程(Linear Congruence Equation)。其中,a、b 和 n 为给定整数,x 为未知数。需要从区间 [0, n-1] 中求解 x,当解不唯一时需要求出全体解。
求解:exgcd
求逆元
求\(a\)模\(p\)的逆元:
答案\(x\)为\(a\)模\(p\)的逆元
中国剩余定理
可求解如下形式的一元线性同余方程组(其中 \(m_1, m_2, \cdots, m_n\) 两两互质):
设 \(m=\prod\nolimits_{i=1}^{n}m_i\),
\(M_i=m/m_i\),
\(t_i\)为线性同余方程 \(M_it_i \equiv 1 \pmod{m_i}\)
的解 \((M_i\) 模 \(m_i\) 的逆元 \()\)
方程有整数解:
矩阵乘法
矩阵定义
一个\(n*m\)矩阵可看作\(n*m\)的二维数组。
矩阵加减
矩阵的加法和减法就是把两个矩阵对应位置的数相加减。
矩阵乘法
设\(A\)为\(n*m\)的矩阵,B为\(m*p\)的矩阵。
若\(C=A*B\),则C为\(n*p\)的矩阵。
计算细则:
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
c[i][j] = 0;
for (int p = 0; p < k; p++)
c[i][j] += a[i][p] * b[p][j];
}
}
矩阵乘法满足结合律与分配律,但不满足交换律
优化递推
设矩阵\(F\)为\(1*n\)的矩阵,\(A\)为\(n*n\)的矩阵,则\(F_0=F*A\)也是\(1*n\)的矩阵。
按照矩阵乘法的运算法则,
\(
\forall j \in [1,n],\)有\(F_{0j}=\sum\limits_{k=1}^{n}F_k*A_{k,j}
\)
,等价于\(F\)每一项按照\(A\)进行了递推。
\(eg:\)
设我们需要进行递推,其中\(f[i]=f[i-1]+2f[i-2]\)
则可以设置矩阵\(F(1*2)\)与\(A(2*2)\),每进行一次转移就是将\(A\)与\(F\)相乘一次。

由于转移一次就是让\(F\)乘上一次\(A\),则转移\(n\)次就是乘上\(n\)个\(A\),即\(F*A^n\),可以使用矩阵快速幂进行优化,将时间复杂度降到log级别。
高斯消元
消元
消元法是将方程组中的一方程的未知数用含有另一未知数的代数式表示,并将其带入到另一方程中,这就消去了一未知数,得到一解;或将方程组中的一方程倍乘某个常数加到另外一方程中去,也可达到消去一未知数的目的。消元法主要用于二元一次方程组的求解。
德国数学家高斯对消元法进行了思考分析,得出了如下结论:
1.在消元法中,参与计算和发生改变的是方程中各变量的系数;
2.各变量并未参与计算,且没有发生改变;
3.可以利用系数的位置表示变量,从而省略变量;
4.在计算中将变量简化省略,方程的解不变。
过程
高斯消元法在将增广矩阵化为最简形后对于自由未知量的赋值,需要掌握线性相关知识,且赋值存在人工经验的因素,使得在学习过程中有一定的困难,将高斯消元法划分为五步骤,从而提出五步骤法,内容如下:
增广矩阵行初等行变换为行最简形;
还原线性方程组;
求解第一个变量;
补充自由未知量;
方法:初等行变换
1.用一个非零数字乘上一行。
2.将一行的若干倍加上另一行。
3。交换两行。
利用高斯消元法五步骤法求解线性方程组
增广矩阵行(初等)变换为行最简形
所谓增广矩阵,即为方程组系数矩阵 A 与常数列 b 的并生成的新矩阵,即 (A | b),增广矩阵行初等变换化为行最简形,即是利用了高斯消元法的思想理念,省略了变量而用变量的系数位置表示变量,增广矩阵中用竖线隔开了系数矩阵和常数列,代表了等于符号。
化为行阶梯形
化为最简形
还原线性方程组
求解第一个变量
补充自由未知量
代码
for(int i=1;i<=n;i++){
int r=i;
for(int j=i+1;j<=n;j++)
if(fabs(map[r][i])<fabs(map[j][i]))
r=j;
if(fabs(map[r][i])<eps){
printf("No Solution");
return 0;
}
if(i!=r)swap(map[i],map[r]);
double div=map[i][i];
for(int j=i;j<=n+1;j++)
map[i][j]/=div;
for(int j=i+1;j<=n;j++){
div=map[j][i];
for(int k=i;k<=n+1;k++)
map[j][k]-=map[i][k]*div;
}
}
ans[n]=map[n][n+1];
for(int i=n-1;i>=1;i--){
ans[i]=map[i][n+1];
for(int j=i+1;j<=n;j++)
ans[i]-=(map[i][j]*ans[j]);
}
线性空间
相关概念
是一个关于以下两个计算封闭的向量集合:
1.向量加法 \(\vec{a}+\vec{b}\)
2.标量乘法 \(\vec{a}*k\)
给定\(k\)个向量\(\vec{a_1},\vec{a_2}...\vec{a_k}\)。若 \(\vec{b}\) 能被这\(k\)个向量用上述两个计算计算出,则称\(\vec{b}\)能被\(\vec{a_1},\vec{a_2}...\vec{a_k}\)表出。所有能够被这 \(k\) 个向量表出的向量构成一个线性空间,这 \(k\) 个向量叫做生成子集。
从线性空间中选出若干向量,若其中存在一个向量能被其它向量表出,则称这些向量线性相关,否则称其为线性无关。
线性无关的生成子集称为线性空间的基底/基。
一个线性空间中,若所有基的大小相等,则称其大小为维数。
与矩阵
对于一个 \(n*m\) 矩阵,若将每行看作一个长度为 \(m\) 的向量,叫做“行向量”。 \(n\) 个行向量产生的线性空间的维数称为 秩。
可以将矩阵进行高斯消元(增广矩阵最后一列看作0),得到一个新的矩阵。新矩阵非零行所构成向量线性无关,因为高斯消元的初等行变换与向量加法与标量乘法等价。可得,新矩阵的所有非零行向量就是一个基,个数就是秩。
组合数学
加法原理
完成一个工程可以有 \(n\) 类办法,\(a_i(1 \le i \le n)\) 代表第 \(i\) 类方法的数目。那么完成这件事共有 \(S=a_1+a_2+\cdots +a_n\) 种不同的方法。
乘法原理
完成一个工程需要分 \(n\) 个步骤,\(a_i(1 \le i \le n)\) 代表第 \(i\) 个步骤的不同方法数目。那么完成这件事共有$ S = a_1 \times a_2 \times \cdots \times a_n $种不同的方法。
排列数
从 \(n\) 个不同元素中,任取 \(m(m\leq n,m\) 与 \(n\) 均为自然数,下同\()\)个元素按照一定的顺序排成一列,叫做从 \(n\) 个不同元素中取出 \(m\) 个元素的一个排列;从 \(n\) 个不同元素中取出 \(m(m\leq n)\) 个元素的所有排列的个数,叫做从 \(n\) 个不同元素中取出 \(m\) 个元素的排列数,用符号
\(\mathrm A_n^m\)(或者是
\(\mathrm P_n^m\))表示。
全排列是排列数的一个特殊情况( \(m=n\) )。
组合数
从 \(n\) 个不同元素中,任取 \(m \leq n\) 个元素组成一个集合,叫做从 \(n\) 个不同元素中取出 \(m\) 个元素的一个组合;从 \(n\) 个不同元素中取出 \(m \leq n\) 个元素的所有组合的个数,叫做从 \(n\) 个不同元素中取出 \(m\) 个元素的组合数,用符号
\(\mathrm C_n^m\) 来表示,读作 \(「n 选 m」\)。
组合数性质
1.$\mathrm C_n^m = \mathrm C_n^{n-m} $
2.\(\mathrm C_n^m = \mathrm C_{n-1}^m + \mathrm C_{n-1}^{m-1}\)
(从取不取 \(n\) 号元素分类)
3.\(\sum_{i=0}^n\mathrm C_n^i = 2^n\) (加法原理)
求法
预处理阶乘。
多重集
包含重复元素的集合,下文皆以 $S = {n_1 \cdot a_1,n_2 \cdot a_2...n_k \cdot a_k} $
多重集排列数
记 \(n=\sum_{i=1}^kn_i\),则 \(S\) 全排列个数为:
多重集组合数
设 \(r \leq n_i(\forall i\in [1,k])\),则从中选 \(r\) 个元素组成一个多重集,产生不同的多重集的数量为:
\(Lucas\) 定理
若 \(p\) 为质数,则对于任意 \(1\leq m \leq n\),
将 \(n\) 与 \(m\) 转换成 \(p\) 进制进行计算。
\(Catalan\)数列
给定 \(n\) 个 \(0\) 与 \(1\) 排列成一个长 \(2n\) 的序列,满足任意前缀中 \(0\) 的个数都不得少于 \(1\) 的个数的序列的数量:
容斥原理
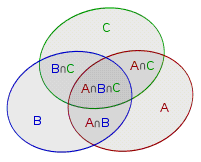
即
\(Mobius\) 函数
设 \(N={p_1}^{c_1}{p_2}^{c_2}...{p_m}^{c_m}\)
定义函数 \(\mu(N)\) 称作 \(Mobius\)函数。
当 \(N\) 包含相等的质因子,\(\mu(N)=0\)
否则,
当 \(N\) 包含偶数个质因子,\(\mu(N)=-1\)
当 \(N\) 包含奇数个质因子,\(\mu(N)=1\)
求解
若只求解一项,可以使用质因数分解。
若要求解多项(如 \(1\) ~ \(N\) 项),可以使用Eratosthenes 筛法。
void getMu() {
mu[1] = 1;
for (int i = 2; i <= n; ++i) {
if (!flg[i]) p[++tot] = i, mu[i] = -1;
for (int j = 1; j <= tot && i * p[j] <= n; ++j) {
flg[i * p[j]] = 1;
if (i % p[j] == 0) {
mu[i * p[j]] = 0;
break;
}
mu[i * p[j]] = -mu[i];
}
}
}
概率与期望
一个随机现象中可能发生的不能再细分的结果被称为 样本点。所有样本点的集合称为 样本空间,通常用 \(\Omega\) 来表示。
一个 随机事件 是样本空间 \(\Omega\) 的子集,它由若干样本点构成,用大写字母 \(A, B, C, \cdots\) 表示。
\(P(A)\) 表示 \(A\) 发生的概率。
期望
若随机变量 \(X\) 有取值 \(x_1,x_2,...\),一个随机事件可表示为 \(X=X_i\),且\(P(X=X_i)=p_i\),则称\(E(x)=\sum p_ix_i\)为变量\(X\)数学期望。
性质
期望为线性函数,满足:
0/1分数规划
分数规划用来求一个分式的极值。
形象一点就是,给出 \(a_i\) 和 \(b_i\),求一组 \(w_i\in\{0,1\}\),最小化或最大化
\(\displaystyle\frac{\sum\limits_{i=1}^na_i\times w_i}{\sum\limits_{i=1}^nb_i\times w_i}\)
另外一种描述:每种物品有两个权值 \(a\) 和 \(b\),选出若干个物品使得
\(\displaystyle\frac{\sum a}{\sum b}\) 最小/最大。
一般分数规划问题还会有一些奇怪的限制,比如『分母至少为 W』。
求解
二分法
分数规划问题的通用方法是二分。
假设我们要求最大值。二分一个答案 mid,然后推式子(为了方便少写了上下界):
那么只要求出不等号左边的式子的最大值就行了。如果最大值比 0 要大,说明 mid 是可行的,否则不可行。
博弈论
Nim 游戏
\(n\) 堆物品,每堆有 \(a_i\) 个,两个玩家轮流取走任意一堆的任意个物品,但不能不取。
取走最后一个物品的人获胜。
这便是一个简单的NIM博弈。游戏过程中面临的状态叫做局面,第一个行动称作先手,第二个称为后手。若在某一局面,无论采取什么措施都将输掉,则称为局面必败。若能在该局面中采取措施使得对手进入必败局面,则称为必胜局面。
NIM博弈没有平局,只有先手必胜与先手必败两种。
定理
当\(A_1 xor A_2 xor... A_n != 0\)时,先手必胜。
公平组合游戏
若一个游戏,有两名玩家交替行动,在游戏进程的任意时刻可执行的行动与轮到哪名玩家无关,无法行动的玩家判负,则为公平组合游戏。NIM就属于此类游戏,常见的棋类不属于此类游戏。
有向图游戏
在一个有向无环图中,只有一个起点,上面有一个棋子,两个玩家轮流沿着有向边推动棋子,不能走的玩家判负。任何一个公平组合游戏都可以转化为有向图游戏。
可以将每一个局面看作一个节点,并向下一个合法局面连一条有向边。
Mex运算与SG函数
定义 \(\operatorname{mex}\) 函数的值为不属于集合 S 中的最小非负整数,即:
例如 \(\operatorname{mex}(\{0, 2, 4\})=1,\operatorname{mex}(\{1, 2\})=0。\)
对于状态 x 和它的所有 k 个后继状态 $y_1, y_2, \ldots, y_k,定义 \operatorname{SG} $函数:
并且游戏整体函数值等于起点的函数值。
局面必败时,\(SG\)值应等于\(0\)。
必胜时,\(SG\)值应大于\(0\)。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号