2022-2024年睿抗CAIP编程技能赛-本科组(国赛)模拟训练题解
题目难度:2022>2024>2023 (个人观点,仅供参考)
感觉这几年的形式大概是开头1道字符串处理/模拟题,然后一道暴力枚举,一道数据结构,一道图论带DP,剩下一道不固定,不排除又来一个dp或者比较复杂的模拟题......
2024年
RC-u1 大家一起查作弊(分数 15)

输入样例:
点击查看代码
static void nnmMNBkf3kfa(){
int fefvB4=2;
int [][]fsdk9A=new int[fefvB4][fefvB4];
fsdk9A[0][0]=1;
for (int gfdgsUB3 = 0; gfdgsUB3 < fefvB4; gfdgsUB3++) {
for (int fdnbXZ8 = 0; fdnbXZ8<fefvB4-gfdgsUB3-1; fdnbXZ8++) {
fsdk9A[gfdgsUB3][fdnbXZ8+1]=fsdk9A[gfdgsUB3][fdnbXZ8]+gfdgsUB3+fdnbXZ8+2;
fsdk9A[gfdgsUB3+1][fdnbXZ8]=fsdk9A[gfdgsUB3][fdnbXZ8]+gfdgsUB3+fdnbXZ8+1;
break;
}
break;
}
}
输出样例:
点击查看代码
155
276 54
思路(字符串处理)
对输入字符串逐字符扫描提取字母数字组成的关键词,并判断其字符类型组合计算可疑分数,再汇总所有关键词的可疑分数、总长度和数量即可。
C++代码实现
点击查看代码
#include <bits/stdc++.h>
#define endl "\n"
using namespace std;
void solve(){
int res=0,sum=0,num=0; // res: 可疑分数总和, sum: 关键词总长度, num: 关键词数量
string s;
while(cin>>s){ // 按单词读取输入
int idx=0;
bool f1=0,f2=0,f3=0; // f1: 是否包含数字, f2: 是否包含小写字母, f3: 是否包含大写字母
int len=0; // 当前关键词长度
while(idx<(int)s.length()){
if(s[idx]>='0'&&s[idx]<='9'){
f1=1;
len++;
}else if(s[idx]>='a'&&s[idx]<='z'){
f2=1;
len++;
}else if(s[idx]>='A'&&s[idx]<='Z'){
f3=1;
len++;
}else { // 遇到非字母数字字符,结束当前关键词
if(len){ // 如果关键词长度大于0,计算分数并更新统计
if(f1&&f2&&f3)res+=5; // 同时包含三种字符类型
else if((f2||f3)&&f1)res+=3; // 包含数字和其他至少一种类型
else if(f2&&f3)res+=1; // 同时包含大小写字母
num++;
sum+=len;
len=f1=f2=f3=0; // 重置状态,准备下一个关键词
}else {
len=f1=f2=f3=0; // 重置状态
}
}
idx++;
}
// 处理行末可能的关键词
if(len){
if(f1&&f2&&f3)res+=5;
else if((f2||f3)&&f1)res+=3;
else if(f2&&f3)res+=1;
num++;
sum+=len;
len=f1=f2=f3=0;
}
}
cout<<res<<endl;
cout<<sum<<" "<<num<<endl;
}
signed main(){
ios::sync_with_stdio(0);cin.tie(0),cout.tie(0);
int _=1;
// cin>>_;
while(_--) solve();
return 0;
}
RC-u2 谁进线下了?II (分数 20)
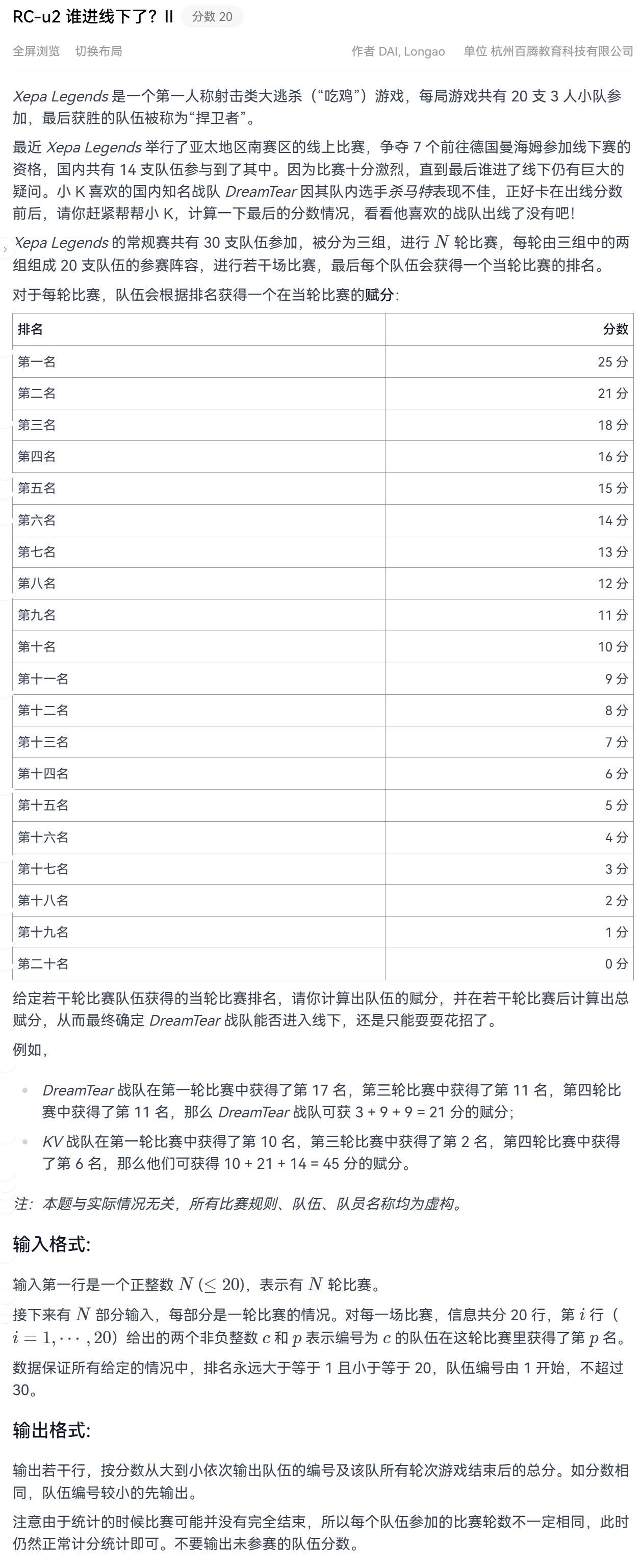
输入样例:
点击查看代码
3
1 1
2 2
9 3
6 4
7 5
11 6
3 7
13 8
8 9
16 10
4 11
19 12
17 13
5 14
12 15
15 16
14 17
10 18
20 19
18 20
5 11
10 12
30 13
22 14
1 1
28 20
21 16
26 17
2 2
24 3
4 4
29 5
8 6
7 15
6 7
3 8
9 9
25 10
23 19
27 18
19 20
26 19
27 18
18 17
21 16
12 15
28 14
20 13
17 12
14 11
13 10
23 9
29 8
22 7
30 6
15 5
24 4
25 3
16 2
11 1
输出样例:
点击查看代码
1 50
2 42
11 39
24 34
16 31
6 29
9 29
25 28
29 27
3 25
4 25
8 25
13 22
30 21
7 20
15 19
22 19
5 15
17 15
14 12
23 12
10 10
12 10
19 8
20 8
21 8
28 6
26 4
27 4
18 3
思路(排序)
利用数组num快速映射排名对应的分数,用数组存储各队伍总分并初始化为-1,累加各队排名对应分数后,对总分非-1的队伍按总分降序、编号升序排序输出即可。
C++代码实现
点击查看代码
#include <bits/stdc++.h>
#define PII pair<int,int>
#define fi first
#define se second
#define endl "\n"
using namespace std;
// 定义排名与分数的映射数组:num[p]表示第p名对应的分数(p从1到20)
int num[30] = {0,25,21,18,16,15,14,13,12,11,10,9,8,7,6,5,4,3,2,1,0};
PII res[31]; // 存储30支队伍的信息(索引1-30对应队伍编号1-30)
// 排序比较函数:先按分数降序,分数相同则按队伍编号升序
bool cmp(PII a, PII b){
if(a.se != b.se) return a.se > b.se;
return a.fi < b.fi;
}
void solve(){
int n;
cin >> n;
// 初始化队伍信息:编号1-30,初始分数设为-1(表示未参赛)
for(int i=1; i<=30; i++){
res[i] = {i, -1};
}
while(n--){
for(int i=1; i<=20; i++){
int c, p; // c:队伍编号,p:排名
cin >> c >> p;
// 计算该队伍在本轮的得分(通过num数组获取)
int score = num[p];
// 更新总分:若未参赛过(分数为-1),直接赋值;否则累加
if(res[c].se == -1){
res[c].se = score;
} else {
res[c].se += score;
}
}
}
sort(res + 1, res + 31, cmp);
for(int i=1; i<=30; i++){
if(res[i].se == -1){
break; // 未参赛队伍排在后面,遇到第一个未参赛的即可停止
}
cout << res[i].fi << " " << res[i].se << endl;
}
}
signed main(){
// 关闭输入输出同步,加速cin/cout(在大量输入时有效)
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
int _ = 1;
// cin >> _;
while(_--){
solve();
}
return 0;
}
RC-u3 势均力敌(分数 25)

输入样例:
点击查看代码
3
5 2 1
输出样例:
点击查看代码
125
512
251
思路(dfs+剪枝)
本题要求将由n(3≤n≤4)个不同个位数字组成的所有n!个n位数分为两组,两组的数字个数均为(n!)/2且平方和相等,最终输出其中一组。
核心思路分为三步:
1. 生成所有可能的 n 位数
通过dfs生成由输入数字组成的所有全排列(即所有可能的n位数)
2. 计算总平方和
遍历aa数组,计算所有n!个数字的平方和,记为maxv。由于题目保证可分为两组平方和相等的集合,因此每组的平方和应为maxv/2,且每组包含n!/2个数字。
3. 查找符合条件的子集
通过dfs筛选出(n!)/2个数字,使得它们的平方和等于maxv/2。搜索过程中通过控制起始索引(避免重复选择)和剪枝(确保剩余数字足够组成目标数量)提高效率,找到符合条件的子集后立即输出。
C++代码实现
点击查看代码
#include <bits/stdc++.h>
#define int long long
#define endl "\n"
using namespace std;
const int N=5e6+10,M=1010,mod=1e9+7,INF=0x3f3f3f3f;
int n; // 输入的n(3或4)
int a[5]; // 存储输入的n个数字
int tt[N]; // 临时数组,在dfs1中存当前排列,在第二个dfs中存选中的数字
int st[N]; // 标记数组,在dfs1中标记数字是否已被使用(1表示已用,0表示未用)
int aa[N]; // 存储所有生成的n位数(全排列结果)
int idx=0; // 记录aa数组中元素的个数(即n!)
int maxv=0; // 所有n位数的平方和总和
int flag=0; // 标记是否找到符合条件的子集(1表示找到)
// 生成所有n位数的全排列,存入aa数组
void dfs1(int x){ // x表示当前要确定第x位数字(1-based)
if(x>n){ // 若已确定n位数字,组成完整的n位数
int tmp=0;
for(int i=1;i<=n;i++){
tmp=tmp*10+tt[i]; // 将tt中存储的数字组合成n位数(如tt[1]=1,tt[2]=2,tt[3]=5→125)
}
aa[idx++]=tmp; // 存入aa数组,索引递增
return ;
}
// 尝试选择未使用的数字放在第x位
for(int i=1;i<=n;i++){
if(st[i]==0){ // 若第i个数字未被使用
st[i]=1; // 标记为已使用
tt[x]=a[i]; // 将第i个数字放在第x位
dfs1(x+1); // 递归确定下一位
st[i]=0; // 回溯:恢复未使用状态,尝试其他数字
}
}
}
// 从aa数组中选idx/2个数字,使其平方和为maxv/2
// x:当前已选数字的个数;h:从aa[h]开始选择(避免重复子集);sum:当前选中数字的平方和
void dfs(int x,int h,int sum){
// 剪枝:若当前平方和的2倍已超过maxv,或已找到解,直接返回
if(sum*2>maxv||flag)return;
// 若已选够idx/2个数字,且平方和为maxv/2(sum*2==maxv)
if(x==idx/2){
if(sum*2==maxv){
// 输出选中的数字
for(int i=0;i<x;i++)cout<<tt[i]<<endl;
flag=1; // 标记已找到解
}
return;
}
// 从h开始遍历aa数组,选择下一个数字
for(int i=h;i<idx;i++){
// 剪枝:确保剩余数字足够选到idx/2个(x + 剩余可选数量 >= idx/2 → x + (idx - i) >= idx/2 → 两边乘2得(x+idx-i)*2 >= idx)
if((x+idx-i)*2>=idx){
tt[x]=aa[i]; // 选中aa[i]
// 递归:已选数量+1,下一次从i+1开始选(避免重复),平方和累加aa[i]^2
dfs(x+1,i+1,sum+tt[x]*tt[x]);
}
if(flag)return; // 若已找到解,直接退出
}
}
void solve(){
cin>>n;
for(int i=1;i<=n;i++)cin>>a[i];
dfs1(1); // 生成所有n位数,存入aa数组
// 计算所有n位数的平方和总和maxv
for(int i=0;i<idx;i++){
maxv+=aa[i]*aa[i];
}
// 查找符合条件的子集并输出
dfs(0,0,0);
}
signed main(){
ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
int _ = 1;
//cin >> _;
while (_--) solve();
return 0;
}
RC-u4 City 不 City (分数 30)

输入样例1:
点击查看代码
8 14 7 8
100 20 30 10 50 80 100 100
7 1 1
7 2 2
7 3 1
7 4 2
1 2 1
1 5 2
2 5 1
3 4 1
3 5 3
3 6 2
4 6 1
5 6 1
5 8 1
6 8 2
输出样例1:
点击查看代码
4 50
输入样例2:
点击查看代码
3 1 1 2
10 20 30
1 3 1
输出样例2:
点击查看代码
Impossible
思路(dijkstra+dp)
本题需找到从起点s到终点t的最优路线,核心目标是:
1:总花销最小;
2:若存在多条最小花销路线,选择途经城镇(除s和t外)的最高旅游热度最小的路线。
为了处理旅游热度,我们需要设计一个dp处理:
一.dp[i]表示:从s到i的所有最小花销路径中,途经城镇(不含s和t)的最高旅游热度的最小值。
二. 状态转移方程:
对当前节点x及邻接节点j(边花销cost):
1.路径更短:
j是终点t:dp[j] = dp[x](t不算途经城镇)。
j是途经城镇:dp[j] = max(dp[x], w[j])(纳入j的热度)。
2.路径等长:
j是终点t:dp[j] = min(dp[j], dp[x])(取更小前序热度)。
j是途经城镇:dp[j] = min(dp[j], max(dp[x], w[j]))(取更小最高热度)。
C++代码实现
点击查看代码
#include <bits/stdc++.h>
#define PII pair<int,int>
#define int long long
#define fi first
#define se second
#define endl "\n"
using namespace std;
const int N=1e5+10, INF=0x3f3f3f3f3f3f3f3f;
int n,m,s,t; // n:城镇数;m:通路数;s:起点;t:终点
int h[N],e[N],ne[N],vv[N],idx; // vv[i]为边的花销
int w[N]; // w[i]为城镇i的旅游热度
int dist[N]; // dist[i]为从s到i的最小花销
int dp[N]; // dp[i]:s到i的最小花销路径中,途经城镇的最高热度的最小值
//int path[N];//记录路径,可省略
void add(int a,int b,int c){
vv[idx] = c,e[idx] = b,ne[idx] = h[a],h[a] = idx++;
}
void dijk(){
memset(dist, 0x3f, sizeof dist);
priority_queue<PII, vector<PII>, greater<PII>> pq;
dist[s] = 0; // 起点s到自身的距离为0
dp[s] = 0; // 起点s无途经城镇,初始最高热度为0
pq.push({0, s});
while(pq.size()){
int x = pq.top().se;
pq.pop();
for(int i = h[x]; ~i; i = ne[i]){
int j = e[i];
int cost = vv[i]; // x到j的花销
// 情况1:发现一条到j的更短路径(总花销更小)
if(dist[j] > dist[x] + cost){
dist[j] = dist[x] + cost;
//path[j]=x;
if(j != t){ // j不是终点t,属于途经城镇
//当前最高热度是前序最高(dp[x])和j的热度(w[j])的较大者
dp[j] = max(w[j], dp[x]);
} else { // j是终点t,不算途经城镇,最高热度与前序一致
dp[j] = dp[x];
}
pq.push({dist[j], j});
}
// 情况2:路径花销相同,需优化最高热度
else if(dist[j]==dist[x]+vv[i]){
//path[j]=x
if(j!=t)dp[j]=min(max(dp[x],w[j]),dp[j]);
else dp[j]=min(dp[j],dp[x]);
//pq.push({dist[j],j});
}
}
}
}
void solve(){
cin >> n >> m >> s >> t;
memset(h, -1, sizeof h);
for(int i = 1; i <= n; i++){
cin >> w[i];
}
while(m--){
int u, v, k;
cin >> u >> v >> k;
add(u, v, k),add(v, u, k);
}
dijk();
if(dist[t] == INF){
cout << "Impossible" << endl;
} else {
cout << dist[t] << " " << dp[t] << endl;
}
}
signed main(){
ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
int _ = 1;
// cin >> _;
while(_--) solve();
return 0;
}
RC-u5 贪心消消乐(分数 30)
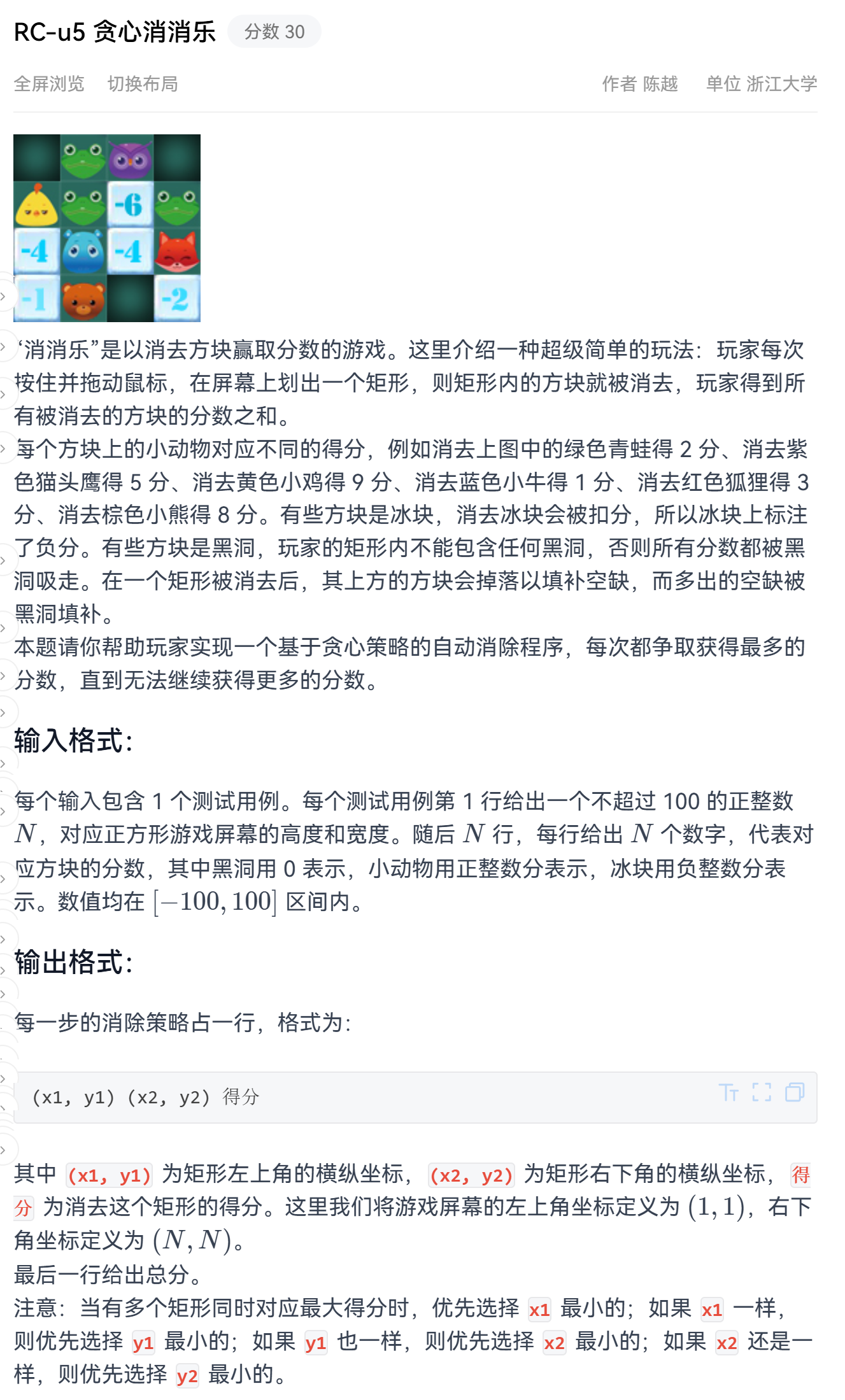
输入样例:
点击查看代码
4
0 2 5 0
9 2 -6 2
-4 1 -4 3
-1 8 0 -2
输出样例:
点击查看代码
(1, 2) (2, 4) 15
(3, 1) (3, 1) 5
(4, 2) (4, 3) 5
(2, 4) (2, 4) 2
27

思路(模拟、前缀和、Kadane's算法[最大子矩形之和问题])
一、步骤:
1.找到和最大的子矩形(不含 0,0 标记为负无穷),若有多个和相等的矩形,选择字典序最小的(左列→上行→右列→下行);
2.消除该矩形(置为 0),剩余元素下落(非 0 元素下沉,填补空白);
3.重复至无有效矩形,输出总分数。
二、对于寻找最大子矩形:
暴力解法: 直接通过四重循环枚举所有可能的矩形(左列、右列、上行、下行),计算每个矩形的和并比较。时间复杂度为 O (n⁴)
Kadane's算法: 将二维问题转化为一维问题。固定上下行(或左右列),计算每列(或每行)在该范围内的和,再用 Kadane 算法找最大子数组(对应最优左右列或上下行)。时间复杂度优化为 O (\(n^3\))Kadane 算法 二维 详解[转载]
注意:
1.输入是按先列后行(j,i)输入的,而不是按先行后列(i,j)!
2.模拟掉落的时候冰块也要掉下去,否则只有21分!!!
C++代码实现
24分暴力代码:O(\(n^4\))
点击查看代码
#include <bits/stdc++.h>
#define int long long
#define LL long long
#define PII pair<int,int>
#define pb push_back
#define fi first
#define se second
#define endl '\n'
using namespace std;
int n,g[110][110]; // g[列][行]存图
int sumg[110][110]; // 前缀和数组加速
void solve() {
cin>>n;
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++){
cin>>g[j][i];
if(g[j][i]==0)g[j][i]=-1e10; // 黑洞标记为负无穷,不会选到,简化逻辑
}
int res=0;
// 循环寻找并消除最大矩形,直到无有效矩形
while(1){
// 计算前缀和
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
sumg[i][j]=g[i][j]+sumg[i-1][j]+sumg[i][j-1]-sumg[i-1][j-1];
PII l={-1,-1},r={-1,-1}; // l:矩形左上角(左列, 上行);r:矩形右下角(右列, 下行)
int maxv=0; // 最大矩形和
// 四重循环暴力枚举所有可能的矩形
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
for(int x=i;x<=n;x++)
for(int y=j;y<=n;y++){
int score=sumg[x][y]-sumg[i-1][y]-sumg[x][j-1]+sumg[i-1][j-1];
if(score<=0)continue;
if(score>maxv)
{
maxv=score;
l={i,j},r={x,y};
}
// 若和相等,按字典序选择更小的矩形(左列→上行→右列→下行)
else if(score==maxv)
{
// 字典序比较逻辑:依次比较左列、上行、右列、下行
if(l.fi!=i){
if(l.fi>i)l={i,j},r={x,y}; // 左列更小,优先选择
}else if(l.se!=j){
if(l.se>j)l={i,j},r={x,y}; // 上行更小,优先选择
}else if(r.fi!=x){
if(r.fi>x)l={i,j},r={x,y}; // 右列更小,优先选择
}else if(r.se!=y){
if(r.se>y)l={i,j},r={x,y}; // 下行更小,优先选择
}
}
}
if(maxv<=0)break; // 无有效矩形,退出循环
res+=maxv;
cout<<"("<<l.fi<<", "<<l.se<<") ("<<r.fi<<", "<<r.se<<") "<<maxv<<endl;
// 消除选中的矩形:将矩形内所有元素置为0
for(int i=l.fi;i<=r.fi;i++)
for(int j=l.se;j<=r.se;j++)
g[i][j]=0;
// 下落逻辑:每列的非0元素下沉(填补被消除的0)
for(int i=1;i<=n;i++) // 按列处理
{
for(int j=n;j>=2;j--) // 从下往上检查,确保下方先填满
if(g[i][j]==0) // 若当前位置为0(空位)
// 向上寻找非0元素,填补当前空位
for(int k=j-1;k>=1;k--)
if(g[i][k]){ // 找到非0元素
g[i][j]=g[i][k]; // 下移元素
g[i][k]=0; // 原位置置为0
break; // 只填补一个,继续处理上方空位
}
}
// 重新标记0为负无穷
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
if(g[i][j]==0)
g[i][j]=-1e10;
}
cout<<res<<endl;
}
signed main() {
std::ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
int _=1;
//cin>>_;
while(_--)solve();
return 0;
}
满分Kadane's 算法优化:O(\(n^3\))
点击查看代码
#include <bits/stdc++.h>
#define int long long
#define LL long long
#define PII pair<int,int>
#define pb push_back
#define fi first
#define se second
#define endl '\n'
using namespace std;
int n,g[110][110];
int sumg[110][110];
int row_sum[110]; // 存储当前上下行范围内每列的和
void solve() {
cin>>n;
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++){
cin>>g[j][i];
if(g[j][i]==0)g[j][i]=-1e10;
}
int res=0;
while(1){
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
sumg[i][j]=g[i][j]+sumg[i-1][j]+sumg[i][j-1]-sumg[i-1][j-1];
PII l={-1,-1},r={-1,-1};
int maxv=0;
// 固定上行j和下行y,用Kadane算法找最优左右列
for(int j=1;j<=n;j++){
memset(row_sum,0,sizeof(row_sum));
for(int y=j;y<=n;y++){
// 计算每列在[j,y]行范围内的和(修复行列对应关系)
for(int i=1;i<=n;i++)
row_sum[i] += g[i][y]; // 累加当前行到列和中
// Kadane算法找最优左右列
int current_sum=0, left=1;
for(int x=1;x<=n;x++){
if(current_sum <= 0){
current_sum = row_sum[x];
left = x;
} else {
current_sum += row_sum[x];
}
// 计算当前矩形实际和(修复和计算错误)
int score = current_sum;
if(score <= 0) continue;
// 更新最大矩形(保持原字典序逻辑)
if(score > maxv){
maxv = score;
l={left,j}; // 左列, 上行
r={x,y}; // 右列, 下行
} else if(score == maxv){
if(l.fi!=left){
if(l.fi>left)l={left,j},r={x,y};
}else if(l.se!=j){
if(l.se>j)l={left,j},r={x,y};
}else if(r.fi!=x){
if(r.fi>x)l={left,j},r={x,y};
}else if(r.se!=y){
if(r.se>y)l={left,j},r={x,y};
}
}
}
}
}
if(maxv<=0)break;
res+=maxv;
cout<<"("<<l.fi<<", "<<l.se<<") ("<<r.fi<<", "<<r.se<<") "<<maxv<<endl;
// 消除选中矩形
for(int i=l.fi;i<=r.fi;i++)
for(int j=l.se;j<=r.se;j++)
g[i][j]=0;
// 下落逻辑(保持原有正确逻辑)
for(int i=1;i<=n;i++){
for(int j=n;j>=2;j--){
if(g[i][j]==0){
for(int k=j-1;k>=1;k--){
if(g[i][k]!=0){
g[i][j]=g[i][k];
g[i][k]=0;
break;
}
}
}
}
}
// 重新标记0为负无穷
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
if(g[i][j]==0)
g[i][j]=-1e10;
}
cout<<res<<endl;
}
signed main() {
std::ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
int _=1;
while(_--)solve();
return 0;
}
[--------------时间分割线--------------]
2023年
RC-u1 睿抗,启动!(分数 15)

输入样例1:
点击查看代码
DOGcat1234XZxzABabFFXIV
输出样例1:
点击查看代码
DOGcat1234XZxzABabFFXIV
ephBZS1234YAwyBCzaggyjw
输入样例2:
点击查看代码
2
DOGcat1234XZxzABabFFXIV
输出样例2:
点击查看代码
DOGcat1234XZxzABabFFXIV
DOGcat1234ZBvxCDYZFFXIV
思路(字符串处理)
严格按照题目要求处理字符串即可。
C++代码实现
点击查看代码
void solve(){
int n;
string s;
cin>>n>>s;
if(s == "yourname") s = "accuber";
cout << s << endl;
// 进行N轮转换
while(n--){
string tmp = "";
int m = (int)s.length();
// 第一轮转换:根据规则替换每个字符
for(int i = 0; i < m; i++){
if(s[i] >= 'A' && s[i] <= 'Z'){
if(s[i] == 'Z') tmp += 'A';
else tmp += (char)(s[i] + 1);
}
else if(s[i] >= 'a' && s[i] <= 'z'){
if(s[i] == 'a') tmp += 'z';
else tmp += (char)(s[i] - 1);
}
else tmp += s[i];
}
s = "";
int idx = 0; // 当前处理位置
// 第二轮转换:处理连续字符
while(idx < m){
int cnt = 0;// 记录连续字符数量
// 处理连续大写字母
while(idx < m && tmp[idx] >= 'A' && tmp[idx] <= 'Z'){
idx++, cnt++;
}
if(cnt){ // 存在连续大写字母
if(cnt >= 3){
for(int i = idx - cnt; i < idx; i++)
s += (char)(tmp[i] - 'A' + 'a');
}
else {
for(int i = idx - cnt; i < idx; i++)
s += tmp[i];
}
continue;
}
// 处理连续小写字母
while(idx < m && tmp[idx] >= 'a' && tmp[idx] <= 'z'){
idx++, cnt++;
}
if(cnt){ // 存在连续小写字母
if(cnt >= 3){
for(int i = idx - cnt; i < idx; i++)
s += (char)(tmp[i] - 'a' + 'A');
}
else {
for(int i = idx - cnt; i < idx; i++)
s += tmp[i];
}
continue;
}
// 处理非字母字符(如数字)
s += tmp[idx++];
}
}
cout << s << endl;
}
RC-u2 桌游猜谜(分数 20)

输入样例:
点击查看代码
2
1
1 1 1 1 1 1
3
1 4 2 8 5 7
2 3 1 4 6 6
4 5 3 2 8 1
输出样例:
点击查看代码
59339
7875
思路(暴力枚举+dfs)
1.枚举询问组合:
颜色:三重循环枚举所有不重复的三色组合(共 20 种)。
范围:枚举所有可能的和范围[L,R](3≤L≤R≤24)。
2.DFS 计算方案数:
递归遍历三色的所有可用数字组合,统计和在[L,R]内的方案数K₁,总方案数减K₁得K₂。
3.计算剩余方案数:
总方案数为(8-n)³,剩余方案数=总方案数-最优询问的Max(K₁,K₂)。
C++代码实现
点击查看代码
#include <bits/stdc++.h>
#define PII pair<int,int>
#define int long long
#define pb push_back
#define fi first
#define se second
#define endl "\n"
using namespace std;
const int N=1e4+10,M=5010,mod=1e9+7,INF=0x3f3f3f3f;
int n,m,k,p;
int a[N][7]; // 存储其他玩家的卡牌信息(未使用)
int card[7][9];// 标记每种颜色的数字是否被使用(行:颜色1-6,列:数字1-8)
PII ans,tmp; // ans存储最优的(K1,K2),tmp存储当前询问的(K1,K2)
int qpow(int a,int b){
int res=1;
while(b){
if(b&1)res=res*a;
a=a*a;
b>>=1;
}
return res;
}
// 计算三种颜色数字和在[L,R]内/外的方案数
//c1,c2,c3为三种颜色;idx为当前处理的颜色索引(1-3);l,r为范围;sum为当前和
void dfs(int c1,int c2,int c3,int idx,int l,int r,int sum){
if(idx>3){ // 已处理完三种颜色,判断和是否在范围内
if(sum>=l&&sum<=r)tmp.fi++; // 在范围内,K1加1
else tmp.se++; // 不在范围内,K2加1
return;
}
int color;
if(idx==1)color=c1;
else if(idx==2)color=c2;
else color=c3;
for(int i=1;i<=8;i++){
if(!card[color][i]){
card[color][i]=1;
dfs(c1,c2,c3,idx+1,l,r,sum+i); // 递归处理下一种颜色,累加当前数字
card[color][i]=0;
}
}
}
// 检查当前询问(三种颜色+范围[L,R])的效果
void check(int c1,int c2,int c3,int l,int r)
{
tmp={0,0};
dfs(c1,c2,c3,1,l,r,0); // 计算K1和K2
// 更新最优解ans:选择Min(K1,K2)最大的情况
if(min(tmp.fi,tmp.se)>min(ans.fi,ans.se))ans=tmp;
else if(tmp.fi==ans.fi&&tmp.se>ans.se)ans=tmp; // 若Min相等,选择K2更大的
else if(tmp.se==ans.se&&tmp.fi>ans.fi)ans=tmp; // 若Min相等,选择K1更大的
}
void solve(){
cin>>n;
memset(card,0,sizeof card);
for(int i=1;i<=n;i++)
for(int j=1;j<=6;j++)
{
cin>>k;
card[j][k]=1; // 标记该数字已被使用
}
ans={-1,-1};
// 枚举所有可能的询问组合
//枚举三种不同颜色
for(int i=1;i<=6;i++)
for(int j=i+1;j<=6;j++)
for(int k=j+1;k<=6;k++)
//枚举范围[L,R](L<=R,和的范围3到24)
for(int l=3;l<=24;l++)
for(int r=l;r<=24;r++)
check(i,j,k,l,r);
// 计算剩余方案数:总方案数*(Max(K1,K2)/总方案数) = Max(K1,K2)
// 注:总方案数为(8-n)^3,而K1+K2=(8-n)^3,故(8-n)^3 * max(K1,K2)/(8-n)^3 = max(K1,K2)
int res=qpow(8-n,3)*max(ans.fi,ans.se);
cout<<res<<endl;
}
signed main(){
ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
int _ = 1;
cin >> _;
while (_--) solve();
return 0;
}
RC-u3 兰州拉面派餐系统(分数 25)

输入样例:
点击查看代码
3 5 10
3 5 8
2 1 3 3 1 1 2 1 3 2
输出样例:
点击查看代码
2:3 5:3 1:5 6:6 3:8 4:8 7:8 8:8 10:13 9:14
3 3 1 1 2
思路(模拟+小根堆排序)
1.堆的维护:用小根堆unuse存空闲篮子(按编号升序),小根堆box存煮面中篮子(按煮好时间升序,时间同则按客单编号升序)。
2.流程处理:处理客单时,优先取unuse中最小编号篮子;无空闲则等box中最早煮好的,释放后再分配,记录煮好时间。
3.结果处理:所有客单处理完后,清空box并记录出锅时间,按送餐时间和客单编号排序输出,同时统计各篮子煮面数量。
C++代码实现
点击查看代码
#include <bits/stdc++.h>
#define PII pair<int,int>
#define int long long
#define pb push_back
#define fi first
#define se second
#define endl "\n"
using namespace std;
const int N=1e6+10,M=5010,mod=1e9+7,INF=0x3f3f3f3f;
int n,m,k,p; // n:面种类数;m:篮子数;k:客单数
int id[N]; // id[i]:第i种面的煮制时间
int cnt[N]; // cnt[i]:第i个篮子煮面数量
vector<PII>ans;// 存储客单编号和送餐时间(用于排序输出)
// num:客单编号、boxnum:篮子编号、time:煮好时间
struct nod{
int num,boxnum,time;
bool operator < (const nod&u)const{
if(time!=u.time)return time>u.time;
return num>u.num;
}
};
priority_queue<int,vector<int>,greater<int>>unuse; // 空闲篮子(小根堆,取编号最小)
priority_queue<nod>box; // 正在煮面的篮子(按规则排序)
// 排序函数:按送餐时间升序,时间相同按客单编号升序
bool cmp(PII a,PII b){
if(a.se!=b.se)return a.se<b.se;
return a.fi<b.fi;
}
void solve(){
cin>>n>>m>>k;
for(int i=1;i<=n;i++)cin>>id[i];
for(int i=1;i<=m;i++)unuse.push(i);
int tt=0; // 记录当前时间(最近一次有面出锅的时间)
for(int i=1;i<=k;i++){
cin>>p;
if(unuse.size()){
int idx=unuse.top();unuse.pop();
//煮好时间=当前时间+面p的煮制时间
box.push({i,idx,id[p]+tt});
}else{
auto tmp=box.top();box.pop();
tt=tmp.time; // 更新当前时间为该面的出锅时间
ans.pb({tmp.num,tt}); // 记录该客单的送餐信息
cnt[tmp.boxnum]++; // 该篮子煮面数量+1
unuse.push(tmp.boxnum);
// 处理同时煮好的其他面(时间相同)
while(box.size()&&box.top().time==tt){
ans.pb({box.top().num,tt});
cnt[box.top().boxnum]++;
unuse.push(box.top().boxnum);
box.pop();
}
// 分配空闲篮子给当前客单
int idx=unuse.top();unuse.pop();
box.push({i,idx,id[p]+tt});
}
}
// 处理剩余所有正在煮面的篮子
while(box.size()){
auto tmp=box.top();box.pop();
tt=tmp.time;
ans.pb({tmp.num,tt});
cnt[tmp.boxnum]++;
unuse.push(tmp.boxnum);
while(box.size()&&box.top().time==tt){
ans.pb({box.top().num,tt});
cnt[box.top().boxnum]++;
unuse.push(box.top().boxnum);
box.pop();
}
}
// 按送餐时间和客单编号排序
sort(ans.begin(),ans.end(),cmp);
cout<<ans[0].fi<<":"<<ans[0].se;
for(int i=1;i<(int)ans.size();i++)
cout<<" "<<ans[i].fi<<":"<<ans[i].se;
cout<<endl;
for(int i=1;i<=m;i++)
cout<<cnt[i]<<(i==m?'\n':' ');
}
signed main(){
ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
int _ = 1;
while (_--) solve();
return 0;
}
RC-u4 拆积木(分数 30)

输入样例1(示意如上图):
点击查看代码
5 5
4 4 4 11 11
9 9 4 2 1
9 5 4 4 4
7 3 3 6 10
8 8 8 10 10
输出样例1:
点击查看代码
11 1 2 4 6 9 5 3 7 8 10
输入样例2:
点击查看代码
4 3
8 9 7
4 4 4
5 6 4
1 4 4
输出样例2:
点击查看代码
7 8 9 Impossible
思路(拓扑排序)
问题本质是求解积木拆卸的拓扑排序。每块积木只能在其正上方的所有积木(若存在且不同编号)被拆除后才能拆卸,即存在 “上方积木→当前积木” 的依赖关系。通过建立依赖图的入度表,使用小根堆优先选择编号最小的可拆积木(入度为 0),最终若所有积木均可拆除则输出顺序,否则输出 “Impossible”。
C++代码实现
点击查看代码
#include <bits/stdc++.h>
#define endl "\n"
using namespace std;
const int N=1e6+10,M=2010,mod=1e9+7,INF=0x3f3f3f3f;
int n,m,k;
int g[M][M]; // 存储积木布局,g[i][j]表示第i行第j列的积木编号
bool st[M][M];// 未使用(预留标记数组)
int d[N]; // d[i]:编号为i的积木的入度(依赖的上方积木数量)
int h[N],e[N],ne[N],idx;
void add(int a,int b){
e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}
void solve()
{
memset(h,-1,sizeof h);
memset(d,-1,sizeof d);
cin>>n>>m;
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
{
cin>>g[i][j];
if(i>1){ // 若不是顶端行,需判断与上方积木的关系
if(g[i-1][j]==g[i][j])continue; // 同一积木,无依赖
// 不同积木:下方积木(g[i][j])依赖上方积木(g[i-1][j])
add(g[i-1][j],g[i][j]);
// 更新下方积木的入度(首次处理则设为1,否则+1)
if(d[g[i][j]]==-1)d[g[i][j]]=1;
else d[g[i][j]]++;
}else{ // 顶端行积木,入度为0(可直接拆除)
if(d[g[i][j]]==-1)d[g[i][j]]=0;
}
}
// 小根堆:存储当前可拆除的积木(入度为0),保证优先取编号最小的
priority_queue<int,vector<int>,greater<int>>pq;
for(int i=1;i<=1e6;i++)
if(d[i]==0)pq.push(i);
bool ans=1;
while(!pq.empty())
{
int p=pq.top();pq.pop();
if(ans)cout<<p,ans=0;
else cout<<" "<<p;
for(int i=h[p];~i;i=ne[i])
{
int j=e[i];
d[j]--;
if(d[j]==0)pq.push(j); // 入度为0则加入可拆队列
}
}
for(int i=1;i<=1e6;i++)
if(d[i]>0){
if(ans)cout<<"Impossible";
else cout<<" Impossible";
return;
}
}
signed main(){
ios::sync_with_stdio(0);cin.tie(0),cout.tie(0);
int _=1;
while(_--) solve();
return 0;
}
RC-u5 栈与数组(分数 30)

输入样例:
点击查看代码
3
6 7 3
1 1 4 5 1 4
1 9 1 9 8 1 0
5 5 2
1 2 3 4 5
6 7 8 9 10
5 5 2
1 1 1 1 1
1 1 1 1 1
输出样例:
点击查看代码
8
10
2
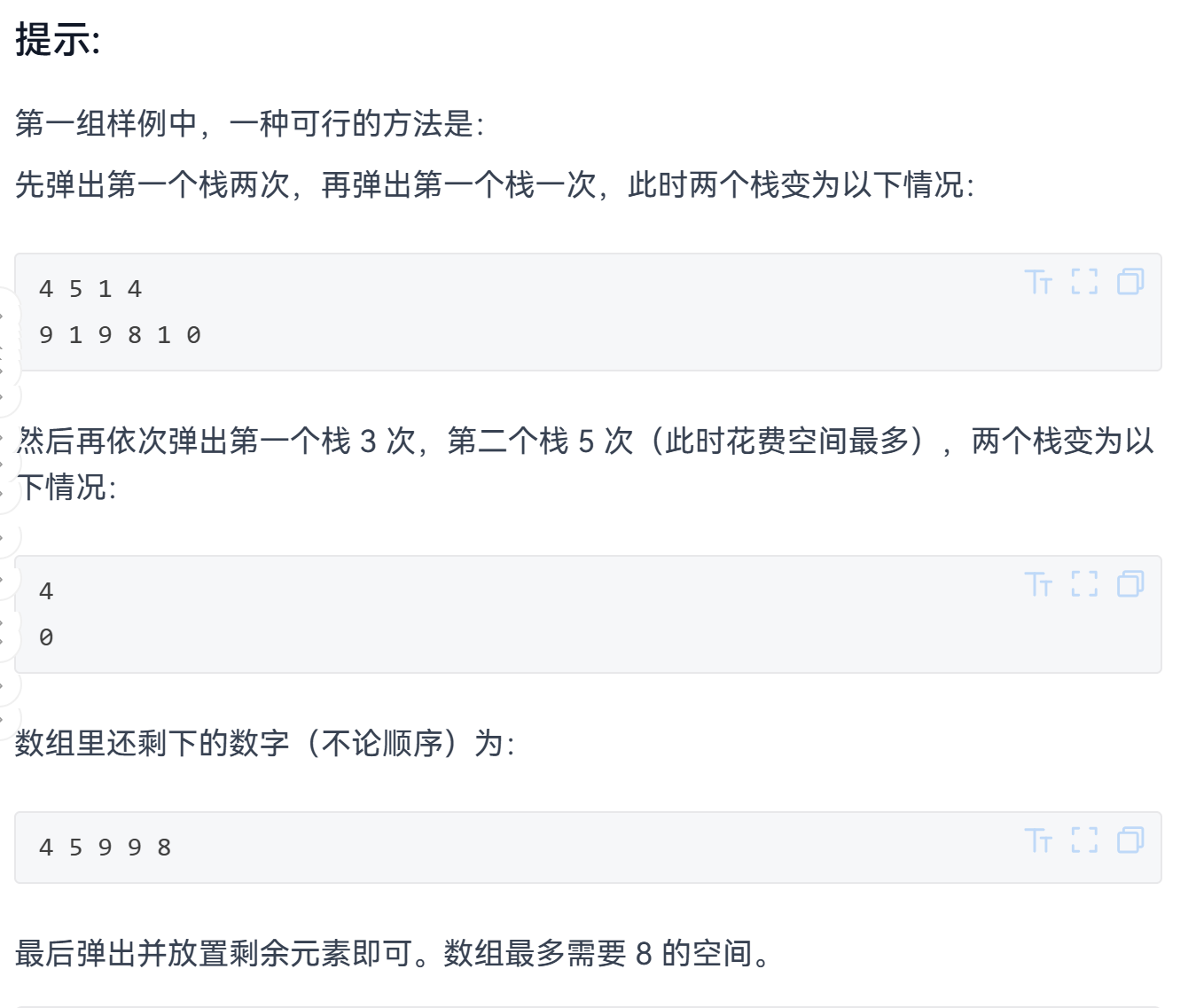
思路(预处理、二分答案+dp)
参考题解
一、pre 数组:预处理剩余元素数
1.核心作用是:计算 “从第一个栈取前 i 个元素、从第二个栈取前 j 个元素” 后,经过所有可能的消除操作(即凑齐 K 个相同元素就删除),最终剩余的元素数量。
2.基础思路:
无论元素从两个栈中以什么顺序取出,最终剩余的元素数是固定的(因为消除只看 “相同元素的总数量”,与顺序无关)。
3.具体计算:
对每个 i(第一个栈取 i 个元素),先处理第一个栈的 i 个元素:
用 cnt 统计每个元素的出现次数,acc 累计当前未消除的元素数。每当某个元素的计数达到 K,就将其计数清零,同时 acc 减去 K(表示消除了 K 个元素)。
再处理第二个栈的 j 个元素:
延续上面的 cnt 和 acc,同样统计并消除,最终得到的 acc 就是 pre[i][j]。
4.示例:
若 K=3,栈 1 前 2 个元素是 [1,1],栈 2 前 1 个元素是 [1]:
处理栈 1 的 2 个1:cnt[1]=2,acc=2;
处理栈 2 的 1 个1:cnt[1]=3(达到K),cnt[1] 清零,acc=2+1-3=0;
因此 pre[2][1] = 0。
二、dp 数组:判断可行性
1.状态定义:
dp[i][j] = 1 表示:存在合法的取法,使得取完第一个栈的 i 个元素和第二个栈的 j 个元素,且过程中数组的临时长度(未消除时的最大长度)始终不超过 x;否则dp[i][j]=0
2.转移逻辑:
dp[i][j] 的值由两种可能的 “最后一步操作” 决定:
最后一步取的是第一个栈的第 i 个元素:
此时前一步的状态是 dp[i-1][j](已取完栈 1 的 i-1 个和栈 2 的 j 个)。
加入第 i 个元素后,临时长度(未消除时)为 pre[i-1][j] + 1(pre[i-1][j] 是前一步消除后的剩余数,加 1 是加入新元素)。
若 pre[i-1][j] + 1 ≤ x 且 dp[i-1][j] = 1,则 dp[i][j] 可行。
最后一步取的是第二个栈的第 j 个元素:
类似地,前一步状态是 dp[i][j-1],加入第 j 个元素后的临时长度为 pre[i][j-1] + 1。
若 pre[i][j-1] + 1 ≤ x 且 dp[i][j-1] = 1,则 dp[i][j] 可行。
3.示例:
若 x=5,pre[2][3] = 4(取 2 个栈 1 和 3 个栈 2 后剩余 4 个),且 dp[1][3] = 1、pre[1][3] + 1 = 3 + 1 = 4 ≤ 5,则 dp[2][3] 可行。
C++代码实现
点击查看代码
#include <bits/stdc++.h>
#define int long long
#define PII pair<int,int>
#define vvi vector<vector<int>>
using namespace std;
const int N=1e3+10,inf=1e10;
int sta1[N],sta2[N],c1,c2,k;
int pre[N][N];//pre[i][j]表示取栈1前i个和栈2前j个元素后剩余的元素数
bool check(int x) // 检查数组长度x是否可行
{
vvi dp(c1+1,vector<int>(c2+1,0));
//dp[i][j]表示:取第一个栈的i个元素和第二个栈的j个元素是否可行(过程中数组临时长度不超过x)
dp[0][0]=1;// 初始状态:取0个元素可行
for(int i=0;i<=c1;i++)
{
for(int j=0;j<=c2;j++)
{
if(!i&&!j) continue; // 跳过初始状态
if(pre[i][j]>x) continue; //剩余元素数超过x,不可行
//从栈1取最后一个元素转移而来
if(i-1>=0&&pre[i-1][j]+1<=x&&dp[i-1][j]) dp[i][j]=1;
//从栈2取最后一个元素转移而来
if(j-1>=0&&pre[i][j-1]+1<=x&&dp[i][j-1]) dp[i][j]=1;
}
}
return dp[c1][c2]==1; //是否能取完所有元素
}
void solve()
{
cin>>c1>>c2>>k;
for(int i=1;i<=c1;i++) cin>>sta1[i];
for(int i=1;i<=c2;i++) cin>>sta2[i];
// 预处理pre数组
for(int i=0;i<=c1;i++)
{
map<int,int> cnt; //统计元素出现次数
int acc=0; //累计剩余元素数
// 处理栈1前i个元素
for(int j=1;j<=i;j++)
{
int v=sta1[j];
cnt[v]++;
acc++;
if(cnt[v]==k){ // 满k个消除
cnt[v]=0;
acc-=k;
}
}
pre[i][0]=acc; // 栈2取0个时的剩余数
// 处理栈2前j个元素
for(int j=1;j<=c2;j++)
{
int v=sta2[j];
cnt[v]++;
acc++;
if(cnt[v]==k)
{ // 满k个消除
cnt[v]=0;
acc-=k;
}
pre[i][j]=acc; // 栈1取i个、栈2取j个时的剩余数
}
}
//二分答案
int l=1,r=c1+c2;
while(l<r)
{
int mid=l+r>>1;
if(check(mid))r=mid;
else l=mid+1;
}
cout<<l<<endl;
}
signed main()
{
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
int _=1;
cin>>_;
while(_--) solve();
return 0;
}
[--------------时间分割线--------------]
2022年
RC-u1 智能红绿灯(分数 15)

输入样例:
点击查看代码
10
3 4 5 6 33 45 49 70 90 100
输出样例:
点击查看代码
18 62
85 129
思路(模拟)
1.遍历所有按钮时间点,维护当前红灯的起始(l)和结束(r)时间,以及是否已延续(flag)。
2.若按钮时间在当前红灯区间外,输出当前区间并生成新区间;若在区间内且未延续,延长红灯并标记已延续。
C++代码实现
点击查看代码
void solve()
{
int n,k; // n:按钮按下次数;k:当前按钮时间点
cin>>n;
int l=0,r=-1; // l:当前红灯起始时间;r:当前红灯结束时间(初始为无效值)
int flag=0; // 标记当前红灯是否已延续(0:未延续;1:已延续)
for(int i=1;i<=n;i++){
cin>>k;
// 若当前按钮时间在当前红灯区间外(需生成新红灯区间)
if(k>r){
if(l!=0)cout<<l<<" "<<r<<endl; // 存在上一个红灯区间
//起始:k+15(15秒后转红);
//结束:k+44(30秒红灯,k+15到k+44共30秒)
l=k+15;
r=k+45-1;
flag=0; // 未延续
}
// 若当前按钮在红灯区间内,且未延续过,延长15秒
else if(flag==0&&k>=l&&k<=r){
r+=15; // 结束时间延长15秒
flag=1; // 标记为已延续
}
}
// 输出最后一个红灯区间
cout<<l<<" "<<r<<endl;
}
RC-u2 女王的大敕令(分数 20)



输入样例:
点击查看代码
2 4 4 2
1 2 3 2
5 3 3 4
输出样例:
点击查看代码
2 1 2 4
2 3 3 1
2 3 3 5
思路(暴力枚举+排序)
1.考虑到数据范围较小(棋盘大小固定为5*5),暴力枚举筛选出起始点(第一次攻击安全)和第一次停留点(第二次攻击安全);
2.暴力枚举筛选出来的起始点与停留点,并验证两点间及停留点到目标点的步长是否符合要求;
3.按规则排序并输出所有有效方案。
C++代码实现
点击查看代码
#include <bits/stdc++.h>
#define PII pair<int,int>
#define pb push_back
#define fi first
#define se second
#define endl "\n"
using namespace std;
const int N=1e6+10,M=2010,mod=1e9+7;
int n,m,k;
int c1,c2,r1,r2; // 北、南、西、东小怪初始位置
int vc1,vc2,vr1,vr2; // 北、南、西、东小怪移动步数
int row,col,d1,d2; // 目标点坐标及两次移动步长
bool g1[6][6],g2[6][6];// g1:第一次攻击危险区域;g2:第二次攻击危险区域
struct nod{
int l,r,ll,rr;
bool operator < (const nod&u)const{
if(l!=u.l)return l<u.l;
if(r!=u.r)return r<u.r;
if(ll!=u.ll)return ll<u.ll;
return rr<u.rr;
}
};
void solve()
{
cin>>c1>>c2>>r1>>r2;
cin>>vc1>>vc2>>vr1>>vr2;
cin>>row>>col>>d1>>d2;
// 计算东西小怪移动后的行
r1-=vr1;
r2+=vr2;
// 标记第一次攻击的危险区域
for(int i=1;i<=5;i++){
g1[r1][i]=g1[r2][i]=1;
g1[i][c1]=g1[i][c2]=1;
}
// 计算南北小怪移动后的列
c1+=vc1;
c2-=vc2;
// 标记第二次攻击的危险区域
for(int i=1;i<=5;i++){
g2[r1][i]=g2[r2][i]=1;
g2[i][c1]=g2[i][c2]=1;
}
// 筛选第一次攻击中安全的起始点(不在g1中)
vector<PII>fir,sec;
for(int i=1;i<=5;i++)
for(int j=1;j<=5;j++)
if(!g1[i][j])
fir.pb({i,j});
// 筛选第二次攻击中安全的第一次停留点(不在g2中)
for(int i=1;i<=5;i++)
for(int j=1;j<=5;j++)
if(!g2[i][j])
sec.pb({i,j});
vector<nod>ans;
for(auto i:fir) // 遍历所有起始点
for(auto j:sec) // 遍历所有停留点
{
// 验证起始点到停留点的步长是否为d1
if(abs(i.fi-j.fi)+abs(i.se-j.se)!=d1)continue;
// 验证停留点到目标点的步长是否为d2
if(abs(j.fi-row)+abs(j.se-col)!=d2)continue;
ans.pb({i.fi,i.se,j.fi,j.se});
}
sort(ans.begin(),ans.end());
for(auto it:ans){
cout<<it.l<<" "<<it.r<<" "<<it.ll<<" "<<it.rr<<endl;
}
}
signed main(){
ios::sync_with_stdio(0);cin.tie(0),cout.tie(0);
int _=1;
//cin>>_;
while(_--) solve();
return 0;
}
RC-u3 战利品分配(分数 25)

输入样例:
点击查看代码
9 11 2 2
100 150 130 50 30 20 200 0 70
1 2
1 3
2 3
2 4
2 5
3 6
4 7
5 7
6 8
7 9
8 9
1 9
输出样例:
点击查看代码
350
思路(BFS+DP)
本题要求在最短路径限制下,选择从起点 S 到终点 T 的路线,使得第 P 位玩家获得的战利品总价值最大。
1.BFS 分层确定最短路径结构
由于路径必须是最短的,我们可以通过BFS计算每个城市到终点的最短距离(层数),并按距离分层存储。最短路径上的城市必然满足:相邻城市的层数差为 1,且终点T的层数是固定的。
2.DP计算最大价值
定义dp[v]表示到达城市v时,第P位玩家累计获得的最大战利品价值。
辅助数组best[v]用于记录能到达 v 的最优前驱城市的dp值(即从上层城市到 v 的最大dp值)。
状态转移:对于第i层的城市v,其dp[v]由上层(i-1层)城市的dp值转移而来。
若i满足i%K==P-1(即v是第P位玩家分配到的城市),则dp[v]需加上v的战利品价值。
// 对于第i层城市v,从i-1层转移
for (int v : layer[i])
{
dp[v]=best[v]; //继承来自i-1层城市的dp值
if (i%K==P-1) // 若v是第P位玩家的分配城市
dp[v]+=w[v]; // 加上v的战利品价值
}
C++代码实现
点击查看代码
#include <bits/stdc++.h>
#define int long long
#define pb push_back
#define fi first
#define se second
#define endl '\n'
using namespace std;
const int N=1e5+10,INF=0x3f3f3f3f3f3f3f3f;
int n,m,k,p,S,T; // n节点数,m边数,k间隔,第p个节点,S起点,T终点
int h[N],e[N<<1],ne[N<<1],w[N],idx;
vector<int> layer[N];// 分层存储节点:layer[i]表示距离起点为i的所有节点
int dp[N],best[N]; // dp[i]:到达节点i的最大权值和;best[i]:节点i的最优前驱权值
int d[N]; // d[i]:节点i到起点的最短距离(层数)
void add(int u,int v){
e[idx]=v,ne[idx]=h[u],h[u]=idx++;
}
void solve()
{
memset(h,-1,sizeof h);
memset(d,-1,sizeof d);
memset(dp,-0x3f,sizeof dp);
memset(best,-0x3f,sizeof best);
cin>>n>>m>>k>>p;
for(int i=1;i<=n;i++)cin>>w[i];
int u,v;
for(int i=0;i<m;i++)
{
cin>>u>>v;
add(u,v);add(v,u);
}
cin>>S>>T;
// BFS分层:计算各节点到起点的最短距离(层数)
layer[0].pb(S);
queue<int>q;
q.push(S);
d[S]=0;
while(!q.empty())
{
int u=q.front();q.pop();
for(int i=h[u];~i;i=ne[i])
{
int v=e[i];
if(d[v]==-1)//未访问
{
d[v]=d[u]+1;
q.push(v);
layer[d[v]].pb(v);//加入对应层数
}
}
}
//按层数从1到终点层数递推
//若p=1(第1个节点),则包含起点权值
dp[S]=(p==1?w[S]:0);
for(int i=1;i<=d[T];i++)
{
//1.计算当前层节点的最优前驱
for(int u:layer[i-1])
{ //遍历上一层所有节点
if(dp[u]==-INF)continue; //跳过不可达节点
// 遍历u的邻接节点,更新当前层节点的best值
for(int j=h[u];~j;j=ne[j])
{
int v=e[j];
// v是当前层节点,且u的权值更大,更新best[v]
if(d[v]==i&&dp[u]>best[v])
best[v]=dp[u];
}
}
//2.更新当前层节点的dp值
for(int v:layer[i])
{
dp[v]=best[v]; //继承最优前驱的权值
//当前层数是第p个间隔节点,加上当前节点权值
if(i%k==p-1)dp[v]+=w[v];
best[v]=-INF;// 重置,避免影响下一层
}
}
cout<<dp[T]<<endl;
}
signed main()
{
ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
int _=1;
//cin>>_;
while(_--)solve();
return 0;
}
RC-u4 变牛的最快方法(分数 30)

输入样例:
点击查看代码
13 5 6 20 2 20 1 13 9 20 3 28 3 34 6 25 233 -1
3 5 6 20 6 20 3 5 9 3 9 20 3 6 6 25 233 -1
输出样例:
点击查看代码
8
122212112023121222

思路(编辑距离问题DP)
本题可转化为经典的编辑距离问题,目标是计算将一个序列通过插入、删除、替换这3种操作转换为另一个序列,求所需的最少操作次数和具体操作序列。
1.DP设计:时间复杂度O(\(n^2\))
定义 dp[i][j] 表示将第一个序列的前 i 个元素转换为第二个序列的前 j 个元素的最少操作次数。
(1)边界条件:
dp[i][0] = i(将前 i 个元素全删除)。
dp[0][j] = j(向空序列插入 j 个元素)。
(2)状态转移:对每个 (i,j),计算三种操作的代价并取最小值:
插入:dp[i][j-1] + 1(在第一个序列第 i 个元素前插入第二个序列第 j 个元素)。
删除:dp[i-1][j] + 1(删除第一个序列第 i 个元素)。
替换 / 不变:dp[i-1][j-1] + (a[i] != b[j])(元素不同则替换,相同则不变)。
2.操作序列获取:
用 op[i][j] 记录到达 (i,j) 状态的操作(0删/1改/2不变/3插)。
用 pre[i][j] 记录前驱状态,从 (n,m) 回溯至 (0,0),反转路径得到操作序列。
C++代码实现
点击查看代码
#include <bits/stdc++.h>
#define int long long
#define LL long long
#define PII pair<int,int>
#define pb push_back
#define fi first
#define se second
#define endl '\n'
using namespace std;
const int N=1e3+10;
int a[N],b[N],n=0,m=0,k;
int dp[N][N]; // dp[i][j]: a前i个转b前j个的最少操作数
int op[N][N]; // op[i][j]: 到达(i,j)的操作(0删1换2留3插)
PII pre[N][N]; // pre[i][j]: (i,j)的前驱状态,用于回溯
void solve() {
while(cin>>k && k!=-1) a[++n] = k;
while(cin>>k && k!=-1) b[++m] = k;
memset(op,-1,sizeof(op));
//初始化:a前i个转空序列(全删)
for(int i=0;i<=n;++i) {
dp[i][0]=i; //需要删i个
op[i][0]=0; //操作0(删)
pre[i][0]={i-1,0}; //前驱是i-1,j=0
}
//初始化:空序列转b前i个(全插)
for(int i=0;i<=m;++i) {
dp[0][i]=i; //需要插i个
op[0][i]=3; //操作3(插)
pre[0][i]={0,i-1}; //前驱是i=0,j-1
}
for(int i=1;i<=n;++i)
{
for(int j=1;j<=m;++j)
{
int op1 = dp[i][j-1]+1; // 插
int op2 = dp[i-1][j]+1; // 删
int op3 = dp[i-1][j-1]+(a[i]!=b[j]); // 换/留
dp[i][j] = min(op1,min(op2,op3)); //取最小代价
// 记录操作和前驱
if(dp[i][j]==op3) { // 换/留
op[i][j] = (a[i]!=b[j] ? 1 : 2); // 不等时换,等时留
pre[i][j] = {i-1,j-1};
} else if(dp[i][j]==op1) { // 插
op[i][j] = 3;
pre[i][j] = {i,j-1};
} else { // 删
op[i][j] = 0;
pre[i][j] = {i-1,j};
}
}
}
// 输出最少操作数
cout<<dp[n][m]<<endl;
// 回溯找操作序列
PII t={n,m};
vector<int> ans;
while(t.fi||t.se) { // 从(n,m)回溯到(0,0)
ans.pb(op[t.fi][t.se]);
t = pre[t.fi][t.se];
}
reverse(ans.begin(),ans.end()); // 反转得到正确顺序
for(auto& it:ans) cout<<it;
cout<<endl;
}
signed main() {
std::ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
int _=1;
// cin>>_;
while(_--) solve();
return 0;
}
RC-u5 养老社区(分数 30)

输入样例:
点击查看代码
11
1 2
1 3
1 4
2 5
2 6
3 7
3 8
4 9
4 10
1 11
1 2 3 4 5 6 7 8 9 9 10
输出样例:
点击查看代码
14
思路(BFS+暴力枚举)
一、题目要求
树中满足以下条件的三元组数量:
三个节点两两距离相等;
三个节点种类各不相同;
三元组本质不同(元素唯一,不重复计数)。
二、关键思路O(\(n^3\))
1.距离计算:利用 BFS 预处理所有节点对的最短距离(树中两点距离唯一)。
2.三元组枚举:通过三重循环枚举所有三元组 (i<j<k),避免重复计数。
两两距离是否相等(d[i][j] == d[i][k] == d[j][k]);
三个节点种类是否全不同(w[i]、w[j]、w[k] 互不相等)。\
注意:三元组枚举的方法实际上会超时,但是题目数据过水,暴力直接过了。。。
C++代码实现
点击查看代码
#include <bits/stdc++.h>
#define PII pair<int,int>
#define int long long
#define pb push_back
#define fi first
#define se second
#define endl "\n"
using namespace std;
// 常量定义:数组大小、模数、无穷大值
const int N=1e6+10,M=2010,mod=1e9+7,INF=0x3f3f3f3f;
const int inf=0x3f3f3f3f3f3f3f3f;
int n,u,v;
int h[N],ne[N*2],e[N*2],idx;
int w[N],d[M][M];// 距离矩阵: d[i][j]表示i到j的最短距离
void add(int a,int b){
e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}
// BFS计算从p到所有节点的最短距离
void bfs(int p){
queue<int>qq;
qq.push(p);
d[p][p]=0;
while(qq.size()){
int idx=qq.front();qq.pop();
for(int i=h[idx];~i;i=ne[i]){
int j=e[i];
if(d[p][j]>d[p][idx]+1){
d[p][j]=d[p][idx]+1;
qq.push(j);
}
}
}
}
void solve(){
memset(h,-1,sizeof h);
memset(d,0x3f,sizeof d);
cin>>n;
for(int i=1;i<n;i++){
cin>>u>>v;
add(u,v),add(v,u);
}
for(int i=1;i<=n;i++)cin>>w[i];
// 计算两两节点间的距离
for(int i=1;i<=n;i++)bfs(i);
int res=0;
// 枚举所有三元组,确保不重复计数
for(int i=1;i<=n;i++)
for(int j=i+1;j<=n;j++)
for(int k=j+1;k<=n;k++)
// 检查两两距离是否相等
if(d[i][j]==d[i][k]&&d[i][j]==d[j][k])
// 检查三个节点种类是否全不同
if(w[i]!=w[j]&&w[i]!=w[k]&&w[j]!=w[k])
res++;
cout<<res<<endl;
}
signed main(){
ios::sync_with_stdio(0);cin.tie(0),cout.tie(0);
int _=1;
// cin>>_;
while(_--)solve();
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号