2022-2024年睿抗(本科组省赛)模拟训练题解
题目难度:2023>2024>2022(个人观点,仅供参考)
2024年
RC-u1 热 热 热

思路(循环+模拟)
循环1~n,判断气温是否大于35°,并按题目要求统计即可
点击查看代码
void solve(){
cin>>n>>k;
int res=0,cnt=0;
for(int i=1;i<=n;i++){
cin>>kk;
if(kk>=35){
if(k==4)cnt++;
else res++;
}
k++;
if(k==8)k=1;
}
cout<<res<<" "<<cnt<<endl;
}
RC-u2 谁进线下了?

输入样例:
点击查看代码
3
6 2
7 3
11 5
10 1
2 9
5 8
14 3
4 3
1 6
18 1
12 1
20 0
13 0
3 2
16 4
8 1
19 0
9 4
17 1
15 0
8 2
19 1
12 2
1 9
10 1
7 5
18 0
14 0
5 2
4 4
2 5
6 2
16 3
13 1
20 0
3 7
9 3
15 0
17 5
11 3
18 0
5 2
2 9
9 4
4 7
10 3
16 0
1 6
20 0
15 1
6 0
3 6
14 3
7 4
19 0
17 0
8 9
11 0
13 5
12 0
输出样例:
点击查看代码
1 9
2 13
3 27
4 30
5 33
6 25
7 4
8 27
9 24
10 12
11 19
12 18
13 8
14 18
15 4
16 17
17 16
18 8
19 12
20 6
思路(模拟)
查表得出排名分,并加上杀敌数得到该场得分,累加到对应队伍的总分中,最后输出即可
点击查看代码
int a[N];
void solve(){
cin>>n;
for(int i=1;i<=n;i++){
for(int j=1;j<=20;j++){
cin>>k>>kk;
if(k==1)a[j]+=12;
else if(k==2)a[j]+=9;
else if(k==3)a[j]+=7;
else if(k==4)a[j]+=5;
else if(k==5)a[j]+=4;
else if(k==6||k==7)a[j]+=3;
else if(k>=8&&k<=10)a[j]+=2;
else if(k<=15)a[j]++;
a[j]+=kk;
}
}
for(int i=1;i<=20;i++)cout<<i<<" "<<a[i]<<endl;
}
RC-u3 暖炉与水豚

思路(模拟,时间复杂度O(N*M))
1.预处理已有的暖炉覆盖区域:遍历所有 'm',标记它们能覆盖的 3×3 区域。
2.已知最多只有一只水豚的状态不太对劲,所有我们只要找到一个隐藏的暖炉即可。如果有且未被覆盖的 'w',说明它周围某个空地可能隐藏了一个暖炉。
3.枚举所有可能藏暖炉的空地 '.':对每个空地,假设放置一个暖炉,再检查是否能让所有水豚的状态都合法,合法则加入答案列表。
小技巧:放置一个暖炉可以把周围标记数组+1,然后恢复-1即可
坑点:放置一个暖炉后不能把冷的水豚变暖了!
点击查看代码
#include <bits/stdc++.h>
#define int long long
#define pb push_back
#define fi first
#define se second
#define endl "\n"
using namespace std;
const int N=1e6+10,M=1010,mod=1e9+7,INF=0x3f3f3f3f;
const int inf=0x3f3f3f3f3f3f3f3f;
int dx[]= {1,0,-1,0},dy[]= {0,1,0,-1};
int n,m,k,kk,u,v;
int st[M][M];
int g[M][M];//0. - 1cold - 2warm 3m
void solve(){
cin>>n>>m;
char c;
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
cin>>c;
if(c=='.')g[i][j]=0;
else if(c=='c')g[i][j]=1;
else if(c=='w')g[i][j]=2;
else {
g[i][j]=3;
for(int l=i-1;l<=i+1;l++){
for(int r=j-1;r<=j+1;r++){
if(l<1||l>n||r<1||r>m)continue;
st[l][r]=1;
}
}
}
}
}
// for(int i=1;i<=n;i++)
// for(int j=1;j<=m;j++){
// cout<<g[i][j];
// if(j!=m)cout<<" ";
// else cout<<endl;
// }
int flag=1;
vector<PII>ans;
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++){
if(g[i][j]==2&&st[i][j]==0){
for(int l=i-1;l<=i+1;l++){
for(int r=j-1;r<=j+1;r++){
if(l<1||l>n||r<1||r>m)continue;
if(g[l][r])continue;
//cout<<l<<" "<<r<<endl;
ans.pb({l,r});
//flag=0;
}
}
}
}
for(PII it:ans){
//cout<<it.fi<<" "<<it.se<<endl;
int flag2=1;
for(int i=it.fi-1;i<=it.fi+1;i++){
for(int j=it.se-1;j<=it.se+1;j++){
if(i<1||i>n||j<1||j>m)continue;
st[i][j]++;
if(g[i][j]==1)
flag2=0;
}
}
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++)
if(g[i][j]==2&&st[i][j]==0)
{
flag2=0;
break;
}
if(flag2==0)break;
}
if(flag2){
cout<<it.fi<<" "<<it.se<<endl;
flag=0;
}
for(int i=it.fi-1;i<=it.fi+1;i++){
for(int j=it.se-1;j<=it.se+1;j++){
if(i<1||i>n||j<1||j>m)continue;
st[i][j]--;
}
}
}
if(flag)cout<<"Too cold!"<<endl;
}
signed main(){
ios::sync_with_stdio(0);cin.tie(0),cout.tie(0);
int _=1;
//cin>>_;
while(_--) solve();
return 0;
}
RC-u4 章鱼图的判断

输入样例:
点击查看代码
3
10 10
1 3
3 5
5 7
7 9
1 2
2 4
2 6
3 8
9 10
1 9
10 10
1 3
3 5
5 7
7 9
9 1
1 2
2 4
4 8
8 10
10 1
10 10
1 3
3 5
5 7
7 9
9 1
2 4
4 8
8 10
10 2
10 6
输出样例:
点击查看代码
Yes 5
No 0
No 2
思路(BFS+拓扑排序)
1.根据题意,我们只要找到环形图和它的节点数,怎么找到这种环形图?
2.首先,可以用BFS分离出各块连通图,环形图一定在其中;
3.其次,考虑拓扑排序,依次把度为1的节点加入队列,对于队头节点,将该节点所连节点的度数-1,所连节点的度数为1时加入队列,最后弹出队头。重复操作直到不存在度为1的节点;
4.再其次,对于剩下节点,如果他们的度数不都为2,那一定不能构造成一个环形图;
5.最后,也是一个坑点,虽然他们的度数不都为2,但是我们还要判断他的节点数是否小于2,因为对于非环形图,没有剩余节点,也就不会有度不为2的剩余节点了
点击查看代码
#include <bits/stdc++.h>
#define PII pair<int,int>
#define int long long
#define pb push_back
#define fi first
#define se second
#define endl "\n"
using namespace std;
const int N=1e6+10,M=1010,mod=1e9+7,INF=0x3f3f3f3f;
int dx[]= {1,0,-1,0},dy[]= {0,1,0,-1};
int n,m,k,kk,u,v;
int h[N],ne[N*2],e[N*2],idx;
int d[N],res;
int st[N];
void add(int a,int b){
e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}
bool bfs(int fir){
queue<int>qq;
vector<int>g;
qq.push(fir);
g.pb(fir);
st[fir]=1;
while(qq.size()){
int idx=qq.front();qq.pop();
for(int i=h[idx];~i;i=ne[i]){
int j=e[i];
if(st[j])continue;
st[j]=1;
qq.push(j);
g.pb(j);
}
}
// for(int i=1;i<=n;i++)cout<<d[i]<<" ";
// cout<<endl;
for(auto it:g){
if(d[it]==1){
qq.push(it);
st[it]=2;
//cout<<it<<" ";
}
}
while(qq.size()){
int idx=qq.front();qq.pop();
for(int i=h[idx];~i;i=ne[i]){
int j=e[i];
if(st[j]==2)continue;
d[j]--;
if(d[j]==1){
//cout<<j<<" ";
qq.push(j);
st[j]=2;
}
}
//cout<<endl;
}
// for(int i=1;i<=n;i++)cout<<d[i]<<" ";
// cout<<endl;
int root=0;
vector<int>gg;
unordered_map<int,bool>mp;
for(auto it:g){
if(d[it]!=2&&st[it]!=2){
return 0;
}else if(d[it]==2&&st[it]==1){
mp[it]=1,root=it;
}
}
int tmp=(int)mp.size();
if(mp.size()<2)return 0;
if(res==0)res=tmp;
return 1;
}
void solve(){
cin>>n>>m;
memset(h,-1,sizeof h);
memset(st,0,sizeof st);
memset(d,0,sizeof d);
idx=0,res=0;
while(m--){
cin>>u>>v;
add(u,v);
add(v,u);
d[u]++,d[v]++;
}
int cnt=0;
for(int i=1;i<=n;i++){
if(st[i])continue;
cnt+=bfs(i);
}
if(cnt==1)cout<<"Yes "<<res<<endl;
else cout<<"No "<<cnt<<endl;
}
signed main(){
ios::sync_with_stdio(0);cin.tie(0),cout.tie(0);
int _=1;
cin>>_;
while(_--) solve();
return 0;
}
RC-u5 工作安排

思路(排序+01背包DP,O(\(N^2\)) )
1.我的01背包DP实际上是一个类背包问题的解法,只不过这里的“容量”是时间,而每个物品(任务)有一个“必须完成的时间限制”
2.设dp[i]表示只考虑前i个工作且考虑第i个工作能获得的最大价值
3.状态转移方程:若 \(j ≥ t_i\),dp[j] = max(dp[j], dp[j - \(t_i\)] + \(p_i\) )
点击查看代码
int dp[5010];
//dp[i]表示只考虑前i个工作且考虑第i个工作能获得的最大价值
struct nod{
int t,d,p;
bool operator <(const nod&u)const{
if(d!=u.d)return d<u.d;
else if(t!=u.t)return t<u.t;
return p>u.p;
}
}tr[N];
void solve(){
cin>>n;
for(int i=1;i<=n;i++){
cin>>tr[i].t>>tr[i].d>>tr[i].p;
}
sort(tr+1,tr+1+n);
memset(dp,0,sizeof dp);
for(int i=1;i<=n;i++){
for(int j=tr[i].d;j>=tr[i].t;j--){
dp[j]=max(dp[j],dp[j-tr[i].t]+tr[i].p);
}
}
int res=0;
for(int i=1;i<=5000;i++){
res=max(res,dp[i]);
}
cout<<res<<endl;
}
signed main(){
ios::sync_with_stdio(0);cin.tie(0),cout.tie(0);
int _=1;
cin>>_;
while(_--) solve();
return 0;
}
[--------------时间分割线--------------]
2023年
RC-u1 亚运奖牌榜
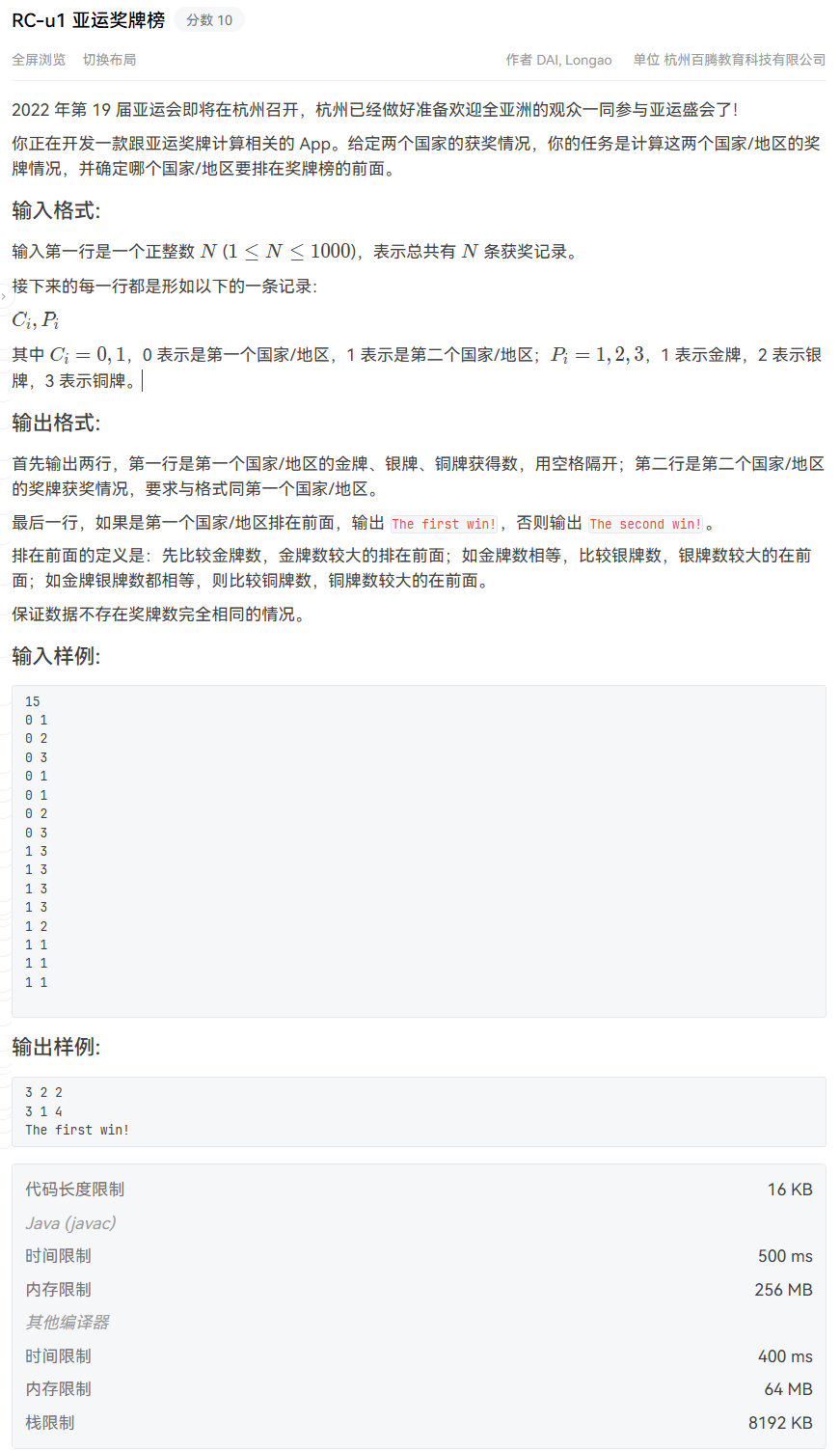
思路(排序)
统计两个国家的金牌、银牌、铜牌数量,并按照金银铜规则排序
点击查看代码
int n,m,k,kk,u,v;
struct nod{
int a[3],id;
bool operator <(const nod&u)const{
if(a[0]!=u.a[0])return a[0]>u.a[0];
else if(a[1]!=u.a[1])return a[1]>u.a[1];
else return a[2]>u.a[2];
}
}tr[2];
void solve(){
cin>>n;
tr[0].id=0;
tr[1].id=1;
for(int i=1;i>=0;i--)
for(int j=0;j<3;j++)
tr[i].a[j]=0;
while(n--){
cin>>k>>kk;
tr[k].a[kk-1]++;
}
sort(tr,tr+2);
if(tr[0].id){
for(int i=1;i>=0;i--){
for(int j=0;j<3;j++){
cout<<tr[i].a[j];
if(j!=2)cout<<" ";
else cout<<endl;
}
}
cout<<"The second win!"<<endl;
}else {
for(int i=0;i<2;i++){
for(int j=0;j<3;j++){
cout<<tr[i].a[j];
if(j!=2)cout<<" ";
else cout<<endl;
}
}
cout<<"The first win!"<<endl;
}
}
RC-u2 出院

思路(模拟,字符串组合匹配)
1.使用一个数组 ss[0~3] 来存储 A~D 四个等级对应的饮料名列表;
2.检查是否是已知饮料,若该饮料已经在任意一个等级中存在,直接输出对应等级
3.枚举所有可能的“前缀”+“后缀”组合;
4.判断前缀是否匹配字符串开头;
5.再判断后缀是否能从该位置开始完全匹配;
6.如果匹配成功,把两个等级拼接起来加入结果列表 ans
点击查看代码
#include <bits/stdc++.h>
#define int long long
#define lc (p<<1)
#define rc (p<<1|1)
#define lowbit(x) (x&-x)
#define pb push_back
#define fi first
#define se second
#define endl "\n"
using namespace std;
const int N=1e6+10,M=1010,mod=1e9+7,INF=0x3f3f3f3f;
int n,m,k,kk,u,v;
vector<string>ss[5];
string s;
void solve(){
cin>>n>>m;
char c;
for(int i=1;i<=n;i++){
cin>>s>>c;
ss[c-'A'].pb(s);
}
while(m--){
cin>>s;
vector<string>ans;
int flag=0;
for(int i=0;i<4;i++){
for(int j=0;j<(int)ss[i].size();j++)
{
if(ss[i][j]!=s)continue;
cout<<(char)(i+'A')<<endl;
flag=1;
break;
}
if(flag)break;
}
if(flag)continue;
for(int i=0;i<4;i++){
for(int j=0;j<(int)ss[i].size();j++){
if(s.find(ss[i][j])!=0)continue;
for(int k=0;k<4;k++){
for(int l=0;l<(int)ss[k].size();l++){
if(ss[i][j].length()+ss[k][l].length()!=s.length())continue;
if(s.find(ss[k][l],(int)ss[i][j].length())!=ss[i][j].length())continue;
string tmp="";
tmp+=(char)(i+'A');
tmp+=(char)(k+'A');
ans.pb(tmp);
}
}
}
}
if((int)ans.size()!=1)cout<<'D'<<endl;
else cout<<ans[0]<<endl;
}
}
signed main(){
ios::sync_with_stdio(0);cin.tie(0),cout.tie(0);
int _=1;
//cin>>_;
while(_--) solve();
return 0;
}
RC-u3 骰子游戏

思路(二进制枚举+全排列枚举,时间复杂度O(\(2^{5}\)\(6^{5}\)10))
1.枚举所有重掷方案dfs1(是否选择重掷)
2.使用dfs生成所有可能的mask方案(骰子重掷后的结果)
3.通过judge()函数计算初始等级和骰子重掷后的等级
4.选择最佳方案:优先选择提升概率最高的方案,若概率相同,选择重掷骰子最少的方案
点击查看代码
#include <bits/stdc++.h>
#define PII pair<int,int>
#define int long long
#define endl "\n"
using namespace std;
const int N=1e6+10,M=1010,mod=1e9+7,INF=0x3f3f3f3f;
int dx[]= {1,0,-1,0},dy[]= {0,1,0,-1};
int n,m,k,kk,u,v;
int h[N],ne[N*2],e[N*2],w[N],idx=0;
int fir,cnt;
struct nod{
double count;
int cnt,l,r;
}ans;
int a[10],num[10],tmp[10],mask[10];
int qpow(int a,int b){
int res=1;
while(b){
if(b&1)res*=a;
a=a*a;
b>>=1;
}
return res;
}
int judge(){
int mp[10]={0};
for(int i=1;i<=5;i++)mp[tmp[i]]++;
int cnt3=0,cnt2=0,cnt1=0;
for(int i=1;i<=6;i++){
if(mp[i]==5)return 8;
else if(mp[i]==4)return 7;
else if(mp[i]==3)cnt3++;
else if(mp[i]==2)cnt2++;
else if(mp[i]==1)cnt1++;
}
if(cnt3==1&&cnt2==1)return 6;
if(mp[2]==1&&mp[3]==1&&mp[4]==1&&mp[5]==1&&mp[6]==1)return 5;
if(mp[2]==1&&mp[3]==1&&mp[4]==1&&mp[5]==1&&mp[1]==1)return 4;
if(cnt3==1)return 3;
if(cnt2==2)return 2;
if(cnt2==1)return 1;
return 0;
}
void dfs(int x){
if(x>5){
// for(int i=1;i<=5;i++)cout<<tmp[i]<<" ";
// cout<<endl;
for(int i=1;i<=5;i++)
if(tmp[i]!=a[i]&&mask[i]==0)return;
if(judge()>fir)cnt++;
return;
}
for(int i=1;i<=6;i++){
tmp[x]=i;
dfs(x+1);
}
}
void dfs1(int x){
if(x>5){
// for(int i=1;i<=5;i++)cout<<mask[i]<<" ";
// cout<<endl;
int cnt1=0;
for(int i=1;i<=5;i++)cnt1+=mask[i];
cnt=0;
dfs(1);
int pp=qpow(6,cnt1);
double count=cnt*1.0/pp;
if(count>ans.count){
ans={count,cnt1,cnt,pp};
}else if(fabs(count-ans.count)<1e-15){
if(cnt1<ans.cnt){
ans={count,cnt1,cnt,pp};
}
}
return;
}
mask[x]=0;
dfs1(x+1);
mask[x]=1;
dfs1(x+1);
}
void solve(){
for(int i=1;i<=5;i++)cin>>a[i],tmp[i]=a[i];
ans={-1,-1,0,1};
fir=judge();
dfs1(1);
int tmp=__gcd(ans.l,ans.r);
ans.l/=tmp,ans.r/=tmp;
cout<<ans.cnt<<" "<<ans.l<<" "<<ans.r<<endl;
}
signed main(){
ios::sync_with_stdio(0);cin.tie(0),cout.tie(0);
int _=1;
cin>>_;
while(_--) solve();
return 0;
}
RC-u4 相对论大师
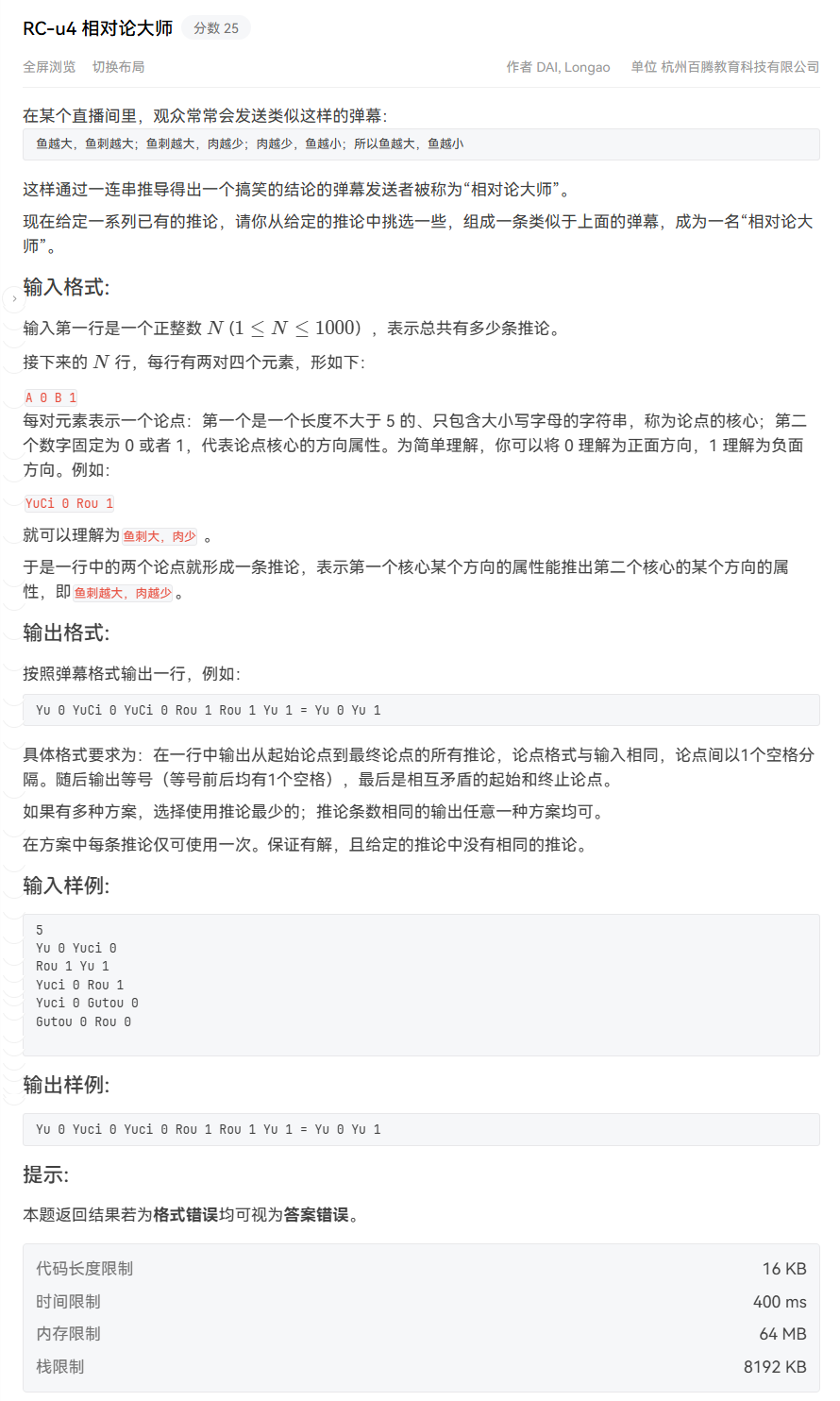
思路(最短路有向图+BFS)
本题难点在于建图
这是一个寻找逻辑矛盾的图论问题。我们需要从给定的一系列推论中找出一个能形成闭环的推理链,使得起点和终点的论点矛盾。
1.将论点转化为图的节点,推论转化为图的边;
2.使用BFS从各顶点遍历图,当发现起点与终点论点相同但方向相反时,视为找到矛盾链;
3.在多条可行路径中选择使用推论最少的路径;
点击查看代码
#include <bits/stdc++.h>
#define int long long
#define pb push_back
#define endl "\n"
using namespace std;
const int N=1e6+10,M=10010,mod=1e9+7,INF=0x3f3f3f3f;
int dx[]= {1,0,-1,0},dy[]= {0,1,0,-1};
int n,m,k,kk,u,v;
int idx,res;
string s;
map<string,int>mp;//mp[string]:论点string对应的数组编号
string mp2[M];//mp[int]:数组编号int对应的论点string
vector<int>gg[M],ans;//邻接表
bool st[M];
/*
3
q1 0 q2 1
q2 0 q1 1
q1 0 q2 0
*/
void bfs(int fir){
queue<vector<int>>qq;
vector<int>tmp;
tmp.pb(fir);
qq.push(tmp);
while(qq.size()){
vector<int> idx=qq.front();qq.pop();
string s1=mp2[fir],s2=mp2[idx.back()];
if(s1.back()=='1'){
s1.back()='0';
}else s1.back()='1';
if(s1==s2){
if(res>(int)idx.size()){
ans=idx;
res=(int)idx.size();
}
continue;
}
vector<int>tmp2=idx;
for(int it:gg[idx.back()]){
int flag=1;
for(int j:tmp2){
if(it==j){
flag=0;
break;
}
}
if(flag==0)continue;
tmp2.pb(it);
qq.push(tmp2);
tmp2.pop_back();
}
}
}
void solve(){
cin>>n;
idx=1;
for(int i=1;i<=n;i++){
string s1,s2;
string c1,c2;
cin>>s1>>c1>>s2>>c2;
s1=s1+" "+c1,s2=s2+" "+c2;
if(mp.find(s1)==mp.end())mp2[idx]=s1,mp[s1]=idx++;
if(mp.find(s2)==mp.end())mp2[idx]=s2,mp[s2]=idx++;
gg[mp[s1]].pb(mp[s2]);
}
// for(auto it:mp){
// cout<<it.se<<" ";
// }
// cout<<endl;
// for(auto it:mp2){
// cout<<it.se<<" ";
// }
// cout<<endl;
res=INF;
for(int i=1;i<idx;i++){
bfs(i);
}
//cout<<res<<endl;
string l=mp2[ans[0]];
string r=mp2[ans.back()];
cout<<l;
for(int i=1;i<(int)ans.size()-1;i++){
cout<<" "<<mp2[ans[i]];
cout<<" "<<mp2[ans[i]];
}
cout<<" "<<r<<" = ";
cout<<l<<" "<<r<<endl;
}
signed main(){
ios::sync_with_stdio(0);cin.tie(0),cout.tie(0);
int _=1;
//cin>>_;
while(_--) solve();
return 0;
}
RC-u5 相对成功与相对失败
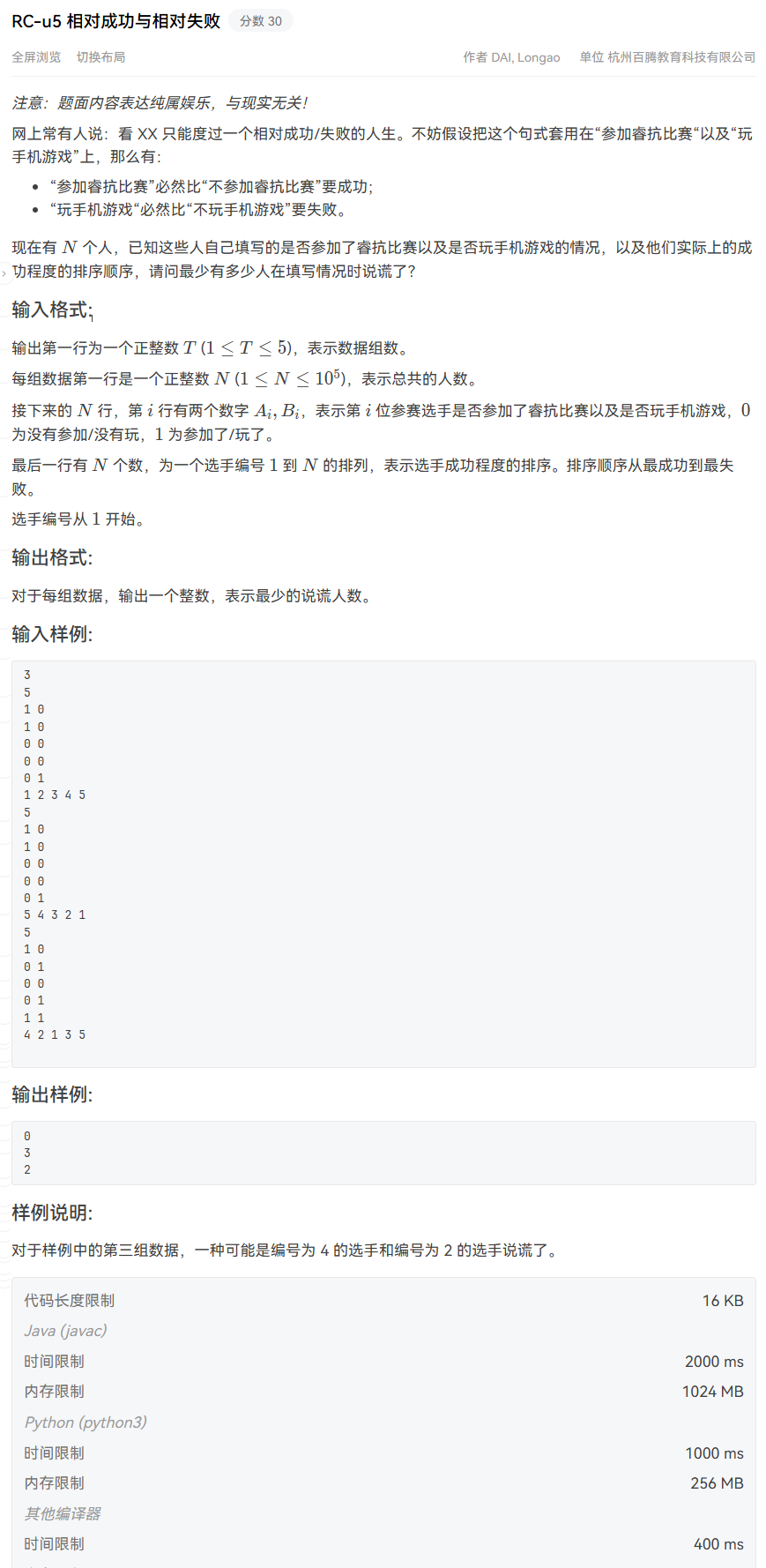
思路(最长不下降子序列DP)
每个学生用二元组 (a, b) 表示其参赛和玩游戏情况。根据题目偏序关系:
(1, 0) > (1, 1)
(1, 0) > (0, 0)
(0, 0) > (0, 1)
其中 (1, 1) 和 (0, 0) 无明确大小关系,可视为等价状态。
1.首先,根据题目偏序关系,成功程度可以分为3个状态:(1,0)>(1,1)|(0,0)>(0,1)
2.我们要找的是一个子序列,使得这个子序列在上述偏序关系下是非递减的。换句话说,不能出现后面的成功程度比前面更低的情况。
3.注意到,把各状态通过val=a-b+1变形后,得到2>1>0,考虑转化为最长不下降子序列问题
4.设dp[val]表示当前以状态值 val 结尾的最长不下降子序列的最大长度。
dp[val] = max(dp[val], dp[val] + 1, dp[val+1] + 1, ..., dp[2] + 1);
5.因为要保留最多的合法子序列,所以最终答案就是:
最少删除的人数 = 总人数 - 最长合法子序列长度
点击查看代码
int num[N];
int dp[3];//dp[i]表示前i个数字中最长不上升子序列长度
/*
ab a-b+1
10 2
00/11 --> 1
01 0
*/
//dp[i]=max(dp[i],dp[num[i]~1]+1)
void solve(){
cin>>n;
for(int i=1;i<=n;i++){
cin>>u>>v;
num[i]=u-v+1;
}
memset(dp,0,sizeof dp);
for(int i=1;i<=n;i++){
cin>>k;
for(int j=num[k];j<=2;j++){
dp[num[k]]=max(dp[num[k]],dp[j]+1);
}
}
int res=0;
for(int i=0;i<=2;i++)res=max(res,dp[i]);
cout<<n-res<<endl;
}
[--------------时间分割线--------------]
2022年
RC-u1 不要浪费金币

思路(模拟)
初始化当前金币数量为 0。
遍历每个怪物带来的金币收益\(P_i\)
如果当前金币 \(P_i\) > m,则进行一次消费(计数加一,金币归零)。
然后加上当前怪物的金币值。
最后输出消费次数。
点击查看代码
void solve(){
cin>>n>>m;
int sum=0,res=0;
while(n--){
cin>>k;
if(sum+k>m)res++,sum=0;
sum+=k;
}
cout<<res<<endl;
}
RC-u2 智能服药助手

思路(模拟)
维护每种药物的上次服用时间;(初始化为负无穷)
根据医嘱的最小间隔时间,判断当前是否可以服用;
如果不能服用(服用时间太近),则输出警告信息;
否则更新最后一次服用时间。
点击查看代码
int a[N],b[N];
void solve(){
cin>>n>>m;
for(int i=1;i<=n;i++)cin>>a[i];
memset(b,-0x3f,sizeof b);
int idx=0;
while(m--){
cin>>idx>>k;
while(k--){
cin>>kk;
if(b[kk]+a[kk]>idx)cout<<"Don't take "<<kk<<" at "<<idx<<"!"<<endl;
else b[kk]=idx;
}
}
}
RC-u3 跑团机器人

思路(字符串模拟)
给定一个仅包含加法、减法和骰子指令的表达式(如 d6+3d5+2-2d3+2d5),你需要:
统计每种面数的骰子需要投掷的个数,并计算该表达式可能得到的结果范围(即最小值和最大值)
- 统一符号格式,让所有项都以 + 或 - 开头,方便统一处理。
2.提取骰子个数(符号后、d前的数字)
3.检查是否是骰子项(是否有d)
4.若为骰子项,继续读取骰子面数,直到遇到下一个符号或结尾
5.骰子项处理记录各面数的骰子的个数,更新最小值和最大值
点击查看代码
#include <bits/stdc++.h>
#define int long long
#define endl "\n"
using namespace std;
const int N=1e6+10,M=10010,mod=1e9+7,INF=0x3f3f3f3f;
int n,m,k,kk,u,v;
int idx,res;
void solve(){
cin>>s;
//小技巧:使得所有项前面都有符号(+ 或 -),方便统一处理。
if(s[0]!='+'&&s[0]!='-')s='+'+s;
int flag=1,minn=0,maxx=0;
int idx=0,l,r;
/*
flag=1 表示当前是加号操作,flag=0 表示是减号操作;
minn 和 maxx 分别记录最终结果的最小值和最大值;
l 表示骰子个数,r 表示骰子面数。
*/
//cout<<s<<endl;
while(idx<(int)s.length())
{
if(s[idx]=='+')flag=1;//判断当前项的符号(加或减)
else flag=0;
idx++;
while(s[idx]!='+'&&s[idx]!='-'&&idx<(int)s.length())//提取骰子个数
{
l=0,r=0;
while(s[idx]!='d'&&s[idx]!='+'&&s[idx]!='-'&&idx<(int)s.length())
{
l=l*10+s[idx]-'0';
idx++;
}
if(s[idx]=='d'){ //检查是否是骰子项(是否有 d)
idx++;//如果是骰子项,继续读取面数 r
while(s[idx]!='+'&&s[idx]!='-'&&idx<(int)s.length())
{
r=r*10+s[idx]-'0';
idx++;
}
}
//cout<<flag<<" "<<l<<"-"<<r<<endl;
// 1 6
// 3 15
// 2 2
// -6 -2
// 2 10
// 2 31
if(r){
if(l==0)l=1;//表示 d6 就是 1d6;
num[r]+=l;
//加号项:最小值 + 个数*1,最大值 + 个数*面数;
//减号项:最小值 - 个数*面数,最大值 - 个数*1;
if(flag)minn+=l,maxx+=l*r;
else minn-=l*r,maxx-=l;
}else {
if(flag)minn+=l,maxx+=l;
else minn-=l,maxx-=l;
}
//cout<<minn<<":"<<maxx<<endl;
if(idx==(int)s.length())break;
}
}
for(int i=1;i<=1000;i++){
if(num[i])cout<<i<<" "<<num[i]<<endl;
}
cout<<minn<<" "<<maxx;
}
signed main(){
ios::sync_with_stdio(0);cin.tie(0),cout.tie(0);
int _=1;
//cin>>_;
while(_--) solve();
return 0;
}
RC-u4 攻略分队

思路(二进制枚举+多条件选最优解)
1.枚举所有可能的分组方式(共 \(2^{6}\)种);
2.用judge() 函数判断当前分组是否满足各层规则,并全局记录最优层
3.统计两队人数和队伍组成情况,并全局保留答案
点击查看代码
#include <bits/stdc++.h>
#define int long long
#define pb push_back
#define fi first
#define se second
#define endl "\n"
using namespace std;
const int N=1e6+10,M=10010,mod=1e9+7,INF=0x3f3f3f3f;
int n,m,k,kk,u,v;
int idx,res;
int ans=0,l=0,r=0;
string ansl,ansr;
bool num[6];
struct nod{
int v;
bool p[3];
//p[0] 对应 主坦克,p[1] 对应工兵,p[2] 对应指挥
}a[6];
//第1支队伍为0,第二支队伍为1
int judge(){
bool p1[3]={0,0,0},p2[3]={0,0,0};
for(int i=0;i<6;i++){
if(num[i]==0){
for(int j=0;j<3;j++){
p1[j]|=a[i].p[j];
}
}else {
for(int j=0;j<3;j++){
p2[j]|=a[i].p[j];
}
}
}
if(p1[2]&&p1[1]&&p2[2]&&p2[1]&&p1[0]&&p2[0])return 3;
if(p1[2]&&p2[2]&&p1[0]&&p2[0])return 2;
if(p1[0]&&p2[0])return 1;
return 0;
}
void dfs(int x){
if(x==6){
int idx=judge();
int peo1=0,peo2=0;
string s1="",s2="",i="";
for(int j=0;j<6;j++){
if(a[j].v==0)continue;
if(num[j]==0)peo1+=a[j].v,s1+=j+'1';
else peo2+=a[j].v,s2+=j+'1';
i+=num[j]+'0';
}
if(idx>ans){//1,2
ansl=s1,ansr=s2;
ans=idx;
l=peo1,r=peo2;
}else if(idx==ans)
{
if(abs(l-r)>abs(peo1-peo2)){//3
ansl=s1,ansr=s2;
ans=idx;
l=peo1,r=peo2;
}else if(abs(l-r)==abs(peo1-peo2)){
if(peo1>=peo2&&l<r){//4
ansl=s1,ansr=s2;
ans=idx;
l=peo1,r=peo2;
}else if(peo1>=peo2&&l>=r){
if(s1<ansl){
ansl=s1,ansr=s2;
ans=idx;
l=peo1,r=peo2;
}
}
}
}
return;
}
num[x]=0;
dfs(x+1);
num[x]=1;
dfs(x+1);
}
void solve(){
for(int i=0;i<6;i++)cin>>a[i].v;
char c;
for(int i=0;i<6;i++)
for(int j=0;j<3;j++){
cin>>c;
a[i].p[j]=c-'0';
}
//000001--111110
dfs(0);
if(ans==0)cout<<"GG"<<endl;
else {
cout<<ansl[0];
for(int i=1;i<(int)ansl.length();i++)cout<<" "<<ansl[i];
cout<<endl;
cout<<ansr[0];
for(int i=1;i<(int)ansr.length();i++)cout<<" "<<ansr[i];
cout<<endl;
}
}
signed main(){
ios::sync_with_stdio(0);cin.tie(0),cout.tie(0);
int _=1;
//cin>>_;
while(_--) solve();
return 0;
}
RC-u5 树与二分图
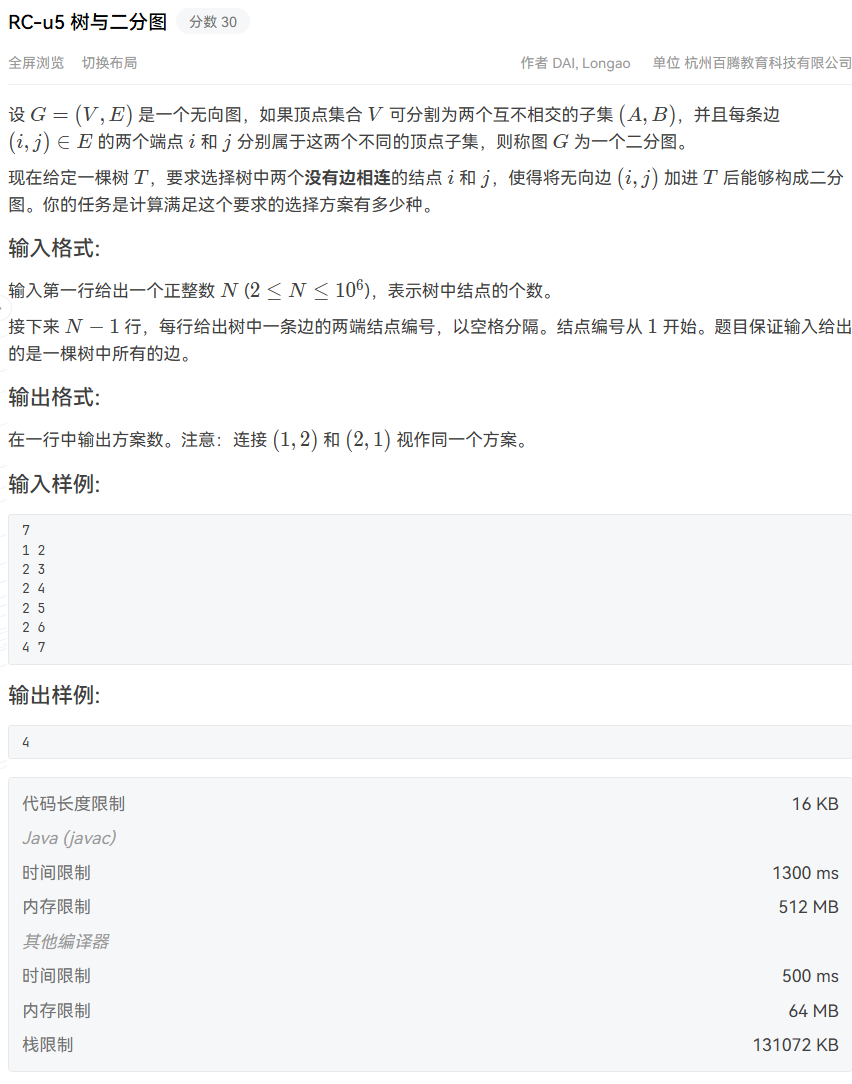
思路(染色法构造二分图)
1.树一定是二分图:因为除根结点外,每个结点有且仅有一个父结点, 所以我们可以把树中的每个结点与它的父结点放到两个不同的集合中, 最后整颗树的结点集都可以划分到两个不相交集合中;
2.对于顶点数为n的二分图, 假设划分的两个集合顶点数分别为m,n-m. 显然这个二分图的最大边数为m*(n-m), 即每个顶点与对面集合所有顶点都形成的边;
3.通过染色法构造二分图,再统计各集合的顶点数n和m,计算答案
点击查看代码
#include <bits/stdc++.h>
#define PII pair<int,int>
#define int long long
#define endl "\n"
using namespace std;
const int N=1e6+10,M=1010,mod=1e9+7,INF=0x3f3f3f3f;
int dx[]= {1,0,-1,0},dy[]= {0,1,0,-1};
int n,m,k,kk,u,v;
int h[N],ne[N*2],e[N*2],w[N],idx=0;
int color[N];
void add(int a,int b){
e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}
bool dfs(int p,int c){
color[p]=c;
for(int i=h[p];~i;i=ne[i]){
int j=e[i];
if(color[j]==0){
if(!dfs(j,3-c))return 0;
}else if(c==color[j])return 0;
}
return 1;
}
void solve(){
cin>>n;
memset(h,-1,sizeof h);
for(int i=1;i<n;i++){
cin>>u>>v;
add(u,v),add(v,u);
}
for(int i=1;i<=n;i++)
if(!color[i])
dfs(i,1);
int res=0;
for(int i=1;i<=n;i++)
if(color[i]==1)res++;
cout<<res*(n-res)-(n-1)<<endl;
}
signed main(){
ios::sync_with_stdio(0);cin.tie(0),cout.tie(0);
int _=1;
// cin>>_;
while(_--) solve();
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号