Codeforces Round 1027 (Div. 3)(A~E)
- 前言: 前天打codeforce挑战第一次不开翻译,感觉其实大部分都是固定的专业名词,除了一些背景故事,不会有太多看不懂的,但是很影响阅读速度,也会导致读得半懂理解错题目意思。所以我第一次还是不出乎意料的翻车了,掉大分了,这不得好好补一下题纪念一下?*
正文:
A题链接

A题大意及做法:
只要从0~\(\sqrt{n}\)遍历一下,判断一下是否可以构造出\((a+b)^2\)=c就可以了,其实用不用字符串读取都可以(虽然赛时我还是转了一下字符串,并且如果成立的一定有a+b=\(\sqrt{n}\),所以只要判断能不能构造a=0,b=\(\sqrt{n}\)就可以了。
//我赛时的代码比较离谱,求我当时的心理状态,赛时代码:
点击查看代码
void solve(){
string s;
cin>>s;
int a=(s[0]-'0')*10+(s[1]-'0'),b=(s[2]-'0')*10+(s[3]-'0');
int c=a*100+b;
int k=sqrt(c);
if(k*k==c){
cout<<0<<" "<<k<<endl;
return;
}
/*
原来我理解错题意了,我那时这里是想判断有没有a^2+b^2=c的,
却写成了(c^2)/(i^4)+i*i=c,还好c是0<=c<=9999的非负整数,
并且c/(i^4)+(i^2)/c==i这个貌似无法成立……
*/
for(int i=1;i*i<=c;i++){
if(c%i==0&&c%i%i==0){
int d=c/i/i;
if(d>i)break;
if(d*d+i*i==c){
cout<<i<<" "<<d<<endl;
return;
}
}
}
//
cout<<-1<<endl;
}
B题链接
B题大意及做法:
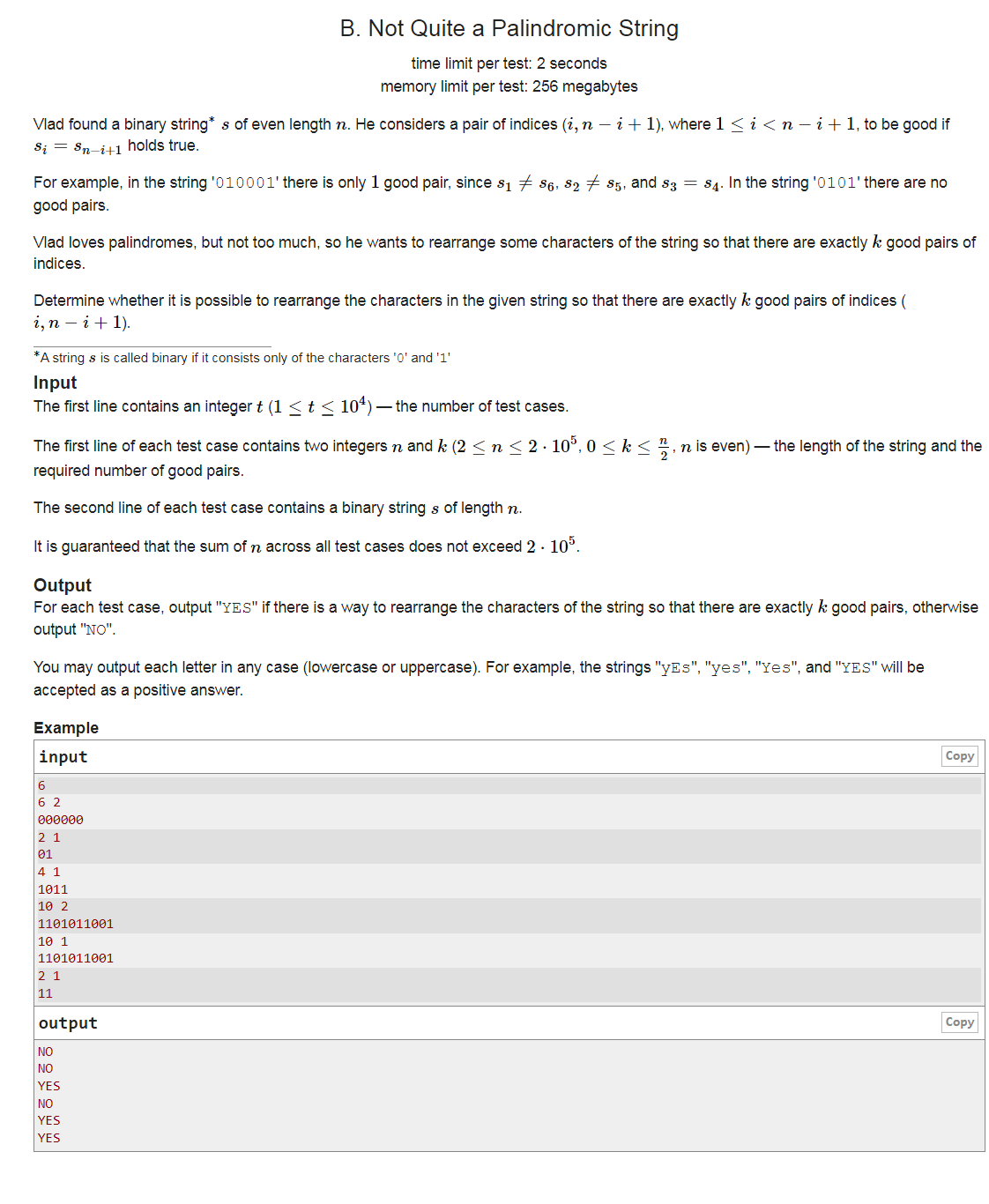
给一个长度为n的01串,我们要判断重新排列字符串中的某些字符,是否可以使得恰好有k个好的索引对。且n为偶数,0<=k<=n/2(这个我竟然没读出来!导致我一直在分类讨论奇偶的情况,被这题卡爆了/(ㄒoㄒ)/~~,虽然偶数情况也错了就是,只能说英语水平有待加强)
索引对:当1<=i<=n-i+1时,若Si==Sn-i+1,则这对(i,n-i+1)是一对索引对。
因为0<=k<=n/2,我们可以把n分为2k和n-2k,2k是构造满足条件的索引对,(n-2k)/2是0和1需要相互抵消的部分,然后遍历一下字符串,记录1的个数cnt1和0的个数cnt0,然后cnt1和cnt0分别减去(n-2*k)/2,如果减成负数了就无法构造,然后判断cnt1/2+cnt0/2是不是等于k,因为1只能和1做一对,0和0做一对,如果不等于k也说明无法构造
补题代码:
点击查看代码
#include <bits/stdc++.h>
#define PII pair<int,int>
#define int long long
#define LL long long
#define lc (p<<1)
#define rc (p<<1|1)
#define lowbit(x) (x&-x)
#define endl "\n"
using namespace std;
const int N=2e5+10,M=1010,mod=1e9+7,INF=0x3f3f3f3f;
const int inf=0x3f3f3f3f3f3f3f3f;
const double eps=1e-6;
int dx[]= {1,0,-1,0},dy[]= {0,1,0,-1};
int n,m,k,kk,u,v;
int h[N],ne[N*2],e[N*2],w[N],idx=0;
string s,ss;
int dp[N][2];
struct node{
int x,y;
int w;
bool operator <(const node&u)const{
return w<u.w;
}
}tr[N];
void add(int a,int b){
e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}
void solve(){
cin>>n>>k;
cin>>s;
int cnt1=0,cnt0=0;
for(int i=0;i<s.length();i++){
if(s[i]=='1')cnt1++;
else cnt0++;
}
int x=(n-2*k)/2;
if(cnt0<x||cnt1<x){
cout<<"NO"<<endl;
return;
}
cnt0-=x,cnt1-=x;
if(cnt0/2+cnt1/2==k)cout<<"YES"<<endl;
else cout<<"NO"<<endl;
}
signed main(){
ios::sync_with_stdio(0);cin.tie(0),cout.tie(0);
int t=1;
cin>>t;
while(t--) solve();
}
C题链接

C题大意及做法:
给一个长度为n的非递减数列a(a[i-1]<=a[i]),让我们把它通过删除元素的操作,分割成一个不连续的数列b(b[i]+1<b[i+1]),求最大数列长度。
我们容易知道,在一个递增且连续的数列里,取数列第1个元素,第3个元素……类似这样隔一个取,不管数列长度n是奇是偶,我们一定能拿到最多的元素,且个数为$\left \lceil n/2 \right \rceil $;我们也知道在这题相等的元素是不能多取的,且1<=ai<=1e6,所以我们可以用一个数组去重(虽然我这里写的是map去重
补题代码:
点击查看代码
#include <bits/stdc++.h>
#define PII pair<int,int>
#define int long long
#define LL long long
#define lc (p<<1)
#define rc (p<<1|1)
#define lowbit(x) (x&-x)
#define endl "\n"
using namespace std;
const int N=1e6+10,M=1010,mod=1e9+7,INF=0x3f3f3f3f;
const int inf=0x3f3f3f3f3f3f3f3f;
const double eps=1e-6;
int dx[]= {1,0,-1,0},dy[]= {0,1,0,-1};
int n,m,k,kk,u,v;
int h[N],ne[N*2],e[N*2],w[N],idx=0;
string s,ss;
struct node{
int x,y;
int w;
bool operator <(const node&u)const{
return w<u.w;
}
}tr[N];
void add(int a,int b){
e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}
void solve(){
cin>>n;
map<int,bool>num;
int minn=1e6,maxx=0;
for(int i=1;i<=n;i++){
cin>>k;
num[k]=1;
}
int flag=0,res=0;
for(auto it:num){
if(num[it.first-1]==0)res++,flag=1;
else if(flag==0){
res++,flag=1;
}else flag=0;
}
cout<<res<<endl;
}
signed main(){
ios::sync_with_stdio(0);cin.tie(0),cout.tie(0);
int t=1;
cin>>t;
while(t--) solve();
}
D题链接
D题大意及做法:
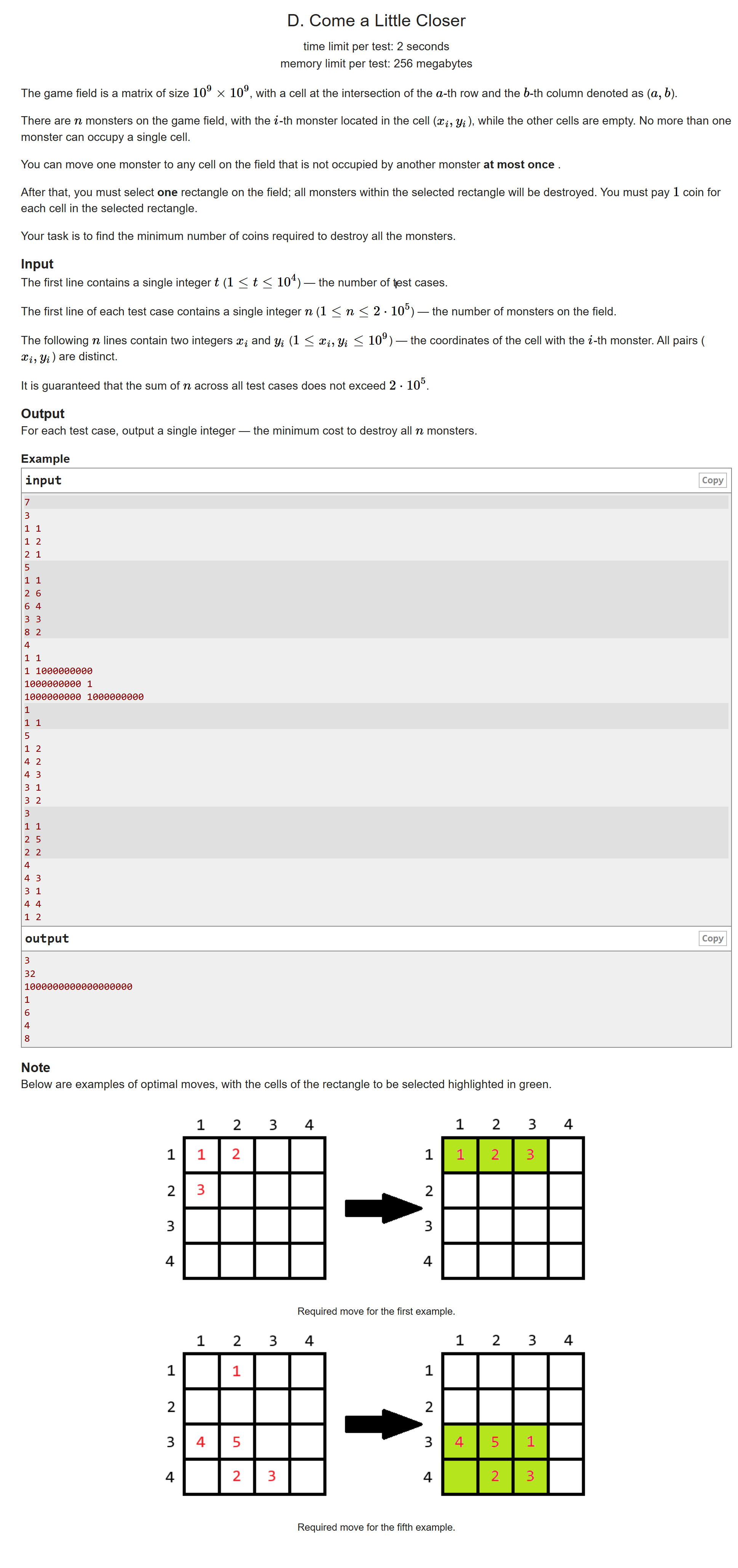
这题有边界问题,写了好久,题目可以抽象成一个1e9 * 1e9大小的网格,有n个点在其中,并且点的坐标不会重复,我们可以移动任意一个点到任意地方最多一次,移动后找到一个矩形能把所有n个点包围起来,找到这样的面积最小的矩形面积。
1.因为只能移动一个点最多一次,在大多数情况,这样的移动相当于去掉这个点,除非所有点在同一条连续的直线上,只需要特判一下这个面积是不是大于n就行了,如果不大于n就加上矩形的长或宽中较小的一个;
2.那去掉哪个点好呢?我们只需要找x坐标最大或最小、y坐标最大或最小的几个点枚举去掉就行了,中间的点对答案是没有影响的,所以我这里找了x坐标最小的和次小的、x坐标最大的和次大的、y坐标最小和次小的、y坐标最大的和次大的,一共八个点,注意这里的次大是不严格的,因为边界上肯定有横坐标或纵坐标相同的两个点。我们找到这些点后,枚举删除其中一个点,然后遍历找到矩形的边界(最小横坐标l,最大横坐标ll,最小纵坐标r,最大纵坐标rr),这样矩形的面积是(|l-ll|+1)*(|r-rr|+1),再加上前面的特判就可以了
补题代码:
点击查看代码
#include <bits/stdc++.h>
#define PII pair<int,int>
#define int long long
#define LL long long
#define lc (p<<1)
#define rc (p<<1|1)
#define lowbit(x) (x&-x)
#define endl "\n"
using namespace std;
const int N=1e6+10,M=1010,mod=1e9+7,INF=0x3f3f3f3f;
const int inf=1e18;
const double eps=1e-6;
int dx[]= {1,0,-1,0},dy[]= {0,1,0,-1};
int n,m,k,kk,u,v;
int h[N],ne[N*2],e[N*2],w[N],idx=0;
PII p[9],a[N];
string s,ss;
struct node{
int x,y;
int w;
bool operator <(const node&u)const{
return w<u.w;
}
}tr[N];
void add(int a,int b){
e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}
void solve(){
cin>>n;
for(int i=1;i<=8;i++)p[i].first=-1;
for(int i=1;i<=n;i++){
cin>>u>>v;
a[i]={u,v};
// cout<<a[i].first<<" "<<a[i].second<<endl;
//x坐标最小的两个点
if(p[1].first==-1||u<p[1].first)p[1]={u,v};
else if(p[2].first==-1||u>=p[1].first&&u<p[2].first)p[2]={u,v};
//y坐标最小的两个点
if(p[3].first==-1||v<p[3].second)p[3]={u,v};
else if(p[4].first==-1||v>=p[3].second&&v<p[4].second)p[4]={u,v};
//x坐标最大的两个点
if(p[5].first==-1||u>p[5].first)p[5]={u,v};
else if(p[6].first==-1||u<=p[5].first&&u>p[6].first)p[6]={u,v};
//y坐标最大的两个点
if(p[7].first==-1||v>p[7].second)p[7]={u,v};
else if(p[8].first==-1||v<=p[7].second&&v>p[8].second)p[8]={u,v};
}
if(n==1){
cout<<1<<endl;
return;
}
int res=inf;
for(int i=1;i<=8;i++){
int l=inf,r=inf,ll=-inf,rr=-inf;
if(p[i].first==-1||p[i].second==-1)continue;
//cout<<p[i].first<<" "<<p[i].second<<endl;
for(int j=1;j<=n;j++){
if(a[j].first==p[i].first&&a[j].second==p[i].second)continue;
l=min(l,a[j].first);
r=min(r,a[j].second);
ll=max(ll,a[j].first);
rr=max(rr,a[j].second);
}
//cout<<l<<" "<<r<<" "<<ll<<" "<<rr<<endl;
if(l==inf||r==inf||ll==-inf||rr==-inf)continue;
res=min(res,(abs(l-ll)+1)*(abs(r-rr)+1));
if(res<n)res+=min(abs(l-ll)+1,abs(r-rr)+1);
}
cout<<res<<endl;
}
signed main(){
ios::sync_with_stdio(0);cin.tie(0),cout.tie(0);
int t=1;
cin>>t;
while(t--) solve();
}
E题链接

E题大意及做法:
感觉E比D好写(在数据结构课上推出来的
题目给出一个n个节点构成的树,根节点的坐标是1,每个节点有一个ai号,代表顶点i的危险程度。顶点的威胁等于从该顶点开始的垂直路径上的最大交替和。我们要求出所以节点到根节点路径上的最大交替和。最大交替和:可以看做是有一个序列1-2-3-4-5-6,那么这其中的最大序列和为1-2+3-4+5
1.这个最大交替和怎么算呢?想来想去可能是树形DP吧,考虑从一个点到根节点之中的最大交替和,又考虑到这个节点(除了根节点)它有一个父节点,它可以由父节点得到,但是如果我们把它的父节点到根节点之中的最大交替和算到上面来,因为是交替加减的,只能得到从这个点到根节点之中的最小交替和,那么我们可以想到他的最大交替和可以由他的父节点的最小交替和得到,那么我们的状态就可以表示出来了:
设dp[i][0]是节点i到根节点之中的最大交替和,dp[i][1]是节点i到根节点之中的最小交替和,w[i]是这个节点的点权,fa[i]是这个节点的父节点:
那么可以推出dp[i][0]=max(w[i],w[i]-dp[fa[i]][1]),dp[i][1]=max(w[i],w[i]-dp[fa[i]][0]);
2.知道状态怎么转移后,我们可以借助树形dp的模板,通过dfs从根节点开始遍历所有节点,在遍历的过程中就可以算出来了
补题代码:
点击查看代码
#include <bits/stdc++.h>
#define PII pair<int,int>
#define int long long
#define LL long long
#define lc (p<<1)
#define rc (p<<1|1)
#define lowbit(x) (x&-x)
#define endl "\n"
using namespace std;
const int N=2e5+10,M=1010,mod=1e9+7,INF=0x3f3f3f3f;
const int inf=0x3f3f3f3f3f3f3f3f;
const double eps=1e-6;
int dx[]= {1,0,-1,0},dy[]= {0,1,0,-1};
int n,m,k,kk,u,v;
int h[N],ne[N*2],e[N*2],w[N],idx=0;//注意如果是无向图的话e[]和ne[]需要开两倍(我这次差点忘记了
string s,ss;
int dp[N][2];
struct node{
int x,y;
int w;
bool operator <(const node&u)const{
return w<u.w;
}
}tr[N];
void add(int a,int b){//链式前向星存图,图论算法必备
e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}
void dfs(int u,int from){//dfs遍历所有的点并且算出他们的最大最小交替和
for(int i=h[u];~i;i=ne[i]){
int j=e[i];
if(j==from)continue;
dp[j][0]=min(w[j]-dp[u][1],w[j]);
dp[j][1]=max(w[j]-dp[u][0],w[j]);
dfs(j,u);
}
}
void solve(){
cin>>n;
for(int i=1;i<=n;i++){
dp[i][0]=dp[i][1]=-INF;
h[i]=-1;
}
idx=0;
for(int i=1;i<=n;i++)cin>>w[i];
for(int i=1;i<n;i++){
cin>>u>>v;
add(u,v),add(v,u);
}
dp[1][0]=0,dp[1][1]=w[1];
dfs(1,0);
for(int i=1;i<=n;i++){
cout<<max(dp[i][0],dp[i][1])<<" ";
}
cout<<endl;
}
signed main(){
ios::sync_with_stdio(0);cin.tie(0),cout.tie(0);
int t=1;
cin>>t;
while(t--) solve();
}
完结撒花!挑战以后也不开翻译!


 浙公网安备 33010602011771号
浙公网安备 33010602011771号