秒啊秒啊--贪心算法

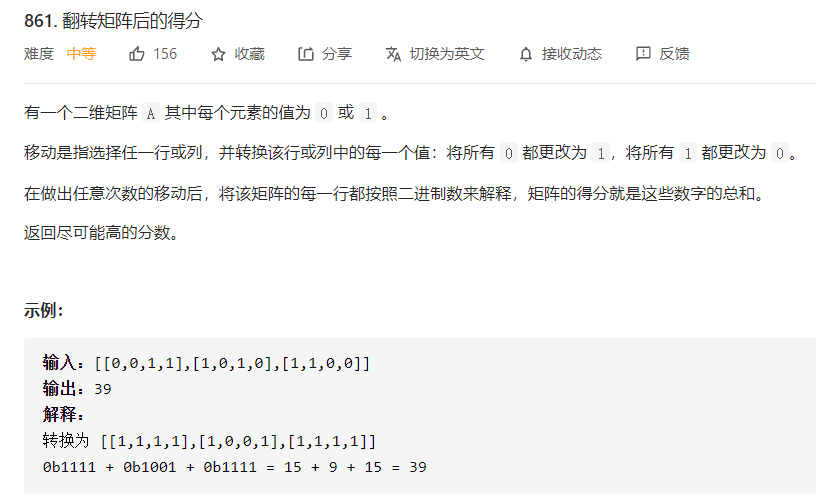
出自lc每日一题--861.翻转矩阵后的得分

原题目地址

分析

第一次尝试做，是根据评论区的思路来的，因为第一眼看完大概知道是用什么方法做，但是具体思路还是没有的。

评论区的思路：

• 第一列值全部转为1，这样结果才能最大化

• 第二列开始就看1的个数，1的个数少于0就当前列值翻转

• 最后遍历数组将每一行值用int保存，然后2转10
  JAVA：考虑用Integer.parseInt(string, 2)进行2转10

总结

按照分析的思路是可以实现的，但是有两个问题：

• 当我们第一列扫过去，翻转后，cnt才能开始计数，可能会习惯性先对A[]先计数

• 第一个问题搞定后，啪的一下提交了，时间复杂度战胜大约5%，这说明算法可以通过，但不是正解

这时候没想到更好解法，直接看官方题解：

• 由于最终只要计算出翻转后的得分，所以我们不用真的修改原数组，只需记录每一列的贡献值即可

• 比如第一列都为1，假设行数为m，列数为n，那么当前列的贡献值就是2^(n -1) * m

• 对于后面每一列，我们取当前列翻转或不翻转最多可以有多少个1，贡献值为2^(n - j - 1)

题解分析部分看完，自己对原来写的%5进行缩减，去掉了修改数组值的部分，最后时间复杂度正解，但是不够精简，
所以看了下题解代码，发现秒啊秒啊，直接双重循环遍历原数组每一元素（从第2列开始），然后每一列取最大1个数
计算贡献值。

class Solution {
    public int matrixScore(int[][] A) {
        int m = A.length, n = A[0].length;
        int ret = m * (1 << (n - 1));

        for (int j = 1; j < n; j++) {
            int nOnes = 0;
            for (int i = 0; i < m; i++) {
                if (A[i][0] == 1) {
                    nOnes += A[i][j];
                } else {
                    nOnes += (1 - A[i][j]); // 如果这一行进行了行反转，则该元素的实际取值为 1 - A[i][j]
                }
            }
            int k = Math.max(nOnes, m - nOnes);
            ret += k * (1 << (n - j - 1));
        }
        return ret;
    }
}

注意：

这里的2^(n - 1/n- j - 1)可以用1 << (n - 1/n - j - 1)代替，很实用。