ST表
本文仅发布于此博客和作者的洛谷博客,不允许任何人以任何形式转载,无论是否标明出处及作者。
0x00 概述
ST表(Sparse Table)是一种基于倍增思想的数据结构,可用于区间查询。
0x10 ST表
0x11 模板
给定一个长度为 \(n\) 的数列,和 \(q\) 次询问,求出每一次询问的区间内数字的最大值。
对于 \(100\%\) 的数据,满足 \(1\le n\le {10}^5\),\(1\le q\le 2\times{10}^6\)。
可以发现,询问的次数明显大于数列长度,线段树每次查询是\(O(\log n)\)的,TLE,无法通过。
0x12 正解: ST表。
我们可以维护这样一个数据结构:
-
建立:设 \(n\) 为数列长度,原数列为
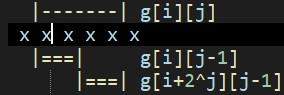
a[i],\(m=\lfloor log_2n\rfloor\).建立一个表格g[n][m],g[i][j]表示区间 \([i,i+2^j-1]\) 中的最大值,即 \(\max\{a[x] \}(x\in[i,i+2^j-1])\). -
初始化:显然,当 \(j=0\) 时,
g[i][j]=a[i]。\(j\neq0\) 时,g[i][j]=max(g[i][j-1],g[i+pow(2,j-1)][j-1])如图。
-
查询:设查询区间左右端点为 \(l,r\) ,长度 \(len=r-l+1\) 。我们在表里找到两个区间 \(t_1,t_2\) ,满足:可重但是不能漏地覆盖 \([l,r]\) 。
显然, \(t_1\) 的左端点是 \(l\) , \(t_2\) 的右端点是 \(r\) 。
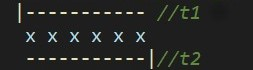
两个区间的一个端点已经分别确定,只需要一个合适的区间长度\(m\)。
设区间长度 \(len=r-l+1\) ,则区间长度\(m\)显然必须满足这些条件:
- \(2m\geq len\),不然没有办法全部覆盖。
- \(m\leq len\),不然 \(t_1,t_2\) 会超过查询区间的边界。
- \(m=2^x\),其中 \(x\in\mathbb{N}\) ,不然 \(t_1,t_2\) 在表格里面找不到。
并且两个区间的长度都为 \(2^{\lfloor \log_2 \rfloor}\) 时,可以满足上面的条件。
\(x=\lfloor \log_2 len\rfloor\)时,符合条件。
此时, \(t_1=[l,l+2^{x}-1],t_2=[r-2^x+1,r]\) ,在
g[n][m]里就分别是t1=g[l][x]和t2=g[r-pow(2,x)+1][x]。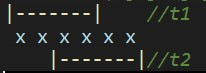
最后的结果就是
max(t1,t2)。
0x13 复杂度分析
空间复杂度:一个 \(\log n\) 行\(n\)列的表,\(n\log n\)。
时间复杂度:初始化时每次\(O(1)\)填入一个g[i][j],表格里有 \(n\log n\) 个数需要计算,所以是 \(O(n\log n)\) 的。查询时\(O(1)\)得到答案。总复杂度是 \(O(n\log n+q)\) 。
可以通过模板题。
0x14 代码
题目:link
#include<bits/stdc++.h>
using namespace std;
int g[100005][17];//log 1e5=16.6
int main(){
int n,m,q;
cin>>n>>q;
m=__lg(n)+1;//st表的行数,__lg(x)可以在O(1)内返回floor(log2(x)).
for(int i=1;i<=n;i++){
cin>>g[i][0];
}
for(int j=1;j<=m;j++){
for(int i=1;i+(1<<j)-1<=n;i++){//区间不能超
g[i][j]=max(g[i][j-1],g[i+(int)pow(2,j-1)][j-1]);
}
}
for(int i=1;i<=q;i++){
int l,r;
cin>>l>>r;
int len=r-l+1;
int x=__lg(len);
int ans=max(g[l][x],g[r-(int)pow(2,x)+1][x]);
cout<<ans<<endl;
}
return 0;
}
轻微卡常(快读,\n,pow改成位运算等)即可通过。
注意:这里初始化最好就这么写,最好不要进行什么额外的操作,不然容易出锅。
0x20 优缺点分析
我们把它和也可以完成区间RMQ的线段树相比。
0x21 优点
-
显然,三个数据结构中,只有ST表能做到O(1)查询,适合在\(q\)很大的时候使用。
-
而且,ST表的码量比线段树少很多,甚至比树状数组还小一点。
0x22 缺点
-
只能计算可重复贡献问题,比如说像最大值这种,\(\max\{[1,6]\}=\max\{\max\{[1,4]\},\max\{[3,6]\}\}\)。 \(3,4\) 被重复计算但是对结果没有影响。可重复贡献问题还有区间按位与,按位或,GCD等。
连一个区间求和都做不成 -
不能做带修的。
0x30 习题
0x31 Problem 1
link:P7333 [JRKSJ R1]JFCA 名字好评
Solution:
首先进行一个破环为链,变成一个长度为\(2n\)的链(经典操作),只存 \(a_i\) , \(b_i\) 不管。
显然,区间 \([k,k+x]\) 的最大值在 \(x\) 递增时,是单调递增的,于是我们可以有以下操作:
对于每一个点 \(i\) ,如果链上的区间 \([i+1,i+n/2]\) 的最大值 \(\geq b_i\) (等价于“存在点 \(j\) 满足 \(j\in[i+1,i+n/2]\land a_j\geq b_i\) ”),那么就在此区间上二分,找到一个满足 \([i+1,j]\) 的最大值 \(\geq b_i\) 且编号尽可能最小的点 \(j\) ,算一下 \(i\) 和 \(j\) 的距离即可。
对于区间 \([i-n/2,i-1]\) 进行相似的操作,所得结果和上面那个区间的结果取个 \(\min\) 就好。(注意进行无解的判断)
区间最大值显然直接使用ST表,\(O(1)\)解决。
另外, \(i-n/2\) 可能是负数,遇到负数直接把区间往右平移 \(n\) 就可以。
#include<bits/stdc++.h>
using namespace std;
struct pt{
int a;
int b;
}a[100007];
int n;
int chain[200014];//链
int st[200014][18];
int query(int l,int r){//查询,l可以不>r,也可以是负数
if(l>r){
swap(l,r);
}
int len=r-l+1;
if(l<=0){
l+=n;
r+=n;
}
int x=__lg(len);
return max(st[l][x],st[r-(1<<x)+1][x]);//经典公式
}
int bs(int k,int l,int r){//[i+1,i+n/2]的二分
if(l==r){
return r-k;
}
int mid=(l+r)/2;
if(query(k+1,mid)<a[k].b){//查询[k+1,mid]有没有解
return bs(k,mid+1,r);
}else{
return bs(k,l,mid);
}
}
int rev_bs(int k,int l,int r){//[i-n/2,i-1]的二分
if(l==r){
return k-r;
}
int mid=(l+r+1)/2;//不+1有死循环(其他方式避免也可以
if(query(k-1,mid)<a[k].b){
return rev_bs(k,l,mid-1);
}else{
return rev_bs(k,mid,r);
}
}
int main(){
cin>>n;
for(int i=1;i<=n;i++){
cin>>a[i].a;
}
for(int i=1;i<=n;i++){
cin>>a[i].b;
}
if(n==1){//n=1要特判
cout<<-1;
return 0;
}
for(int i=1;i<=n;i++){
chain[i]=a[i].a;
}
for(int i=1;i<=n;i++){//再复制一遍,长度变成2n
chain[i+n]=a[i].a;
}
for(int i=1;i<=2*n;i++){
st[i][0]=chain[i];
}
for(int j=1;j<=18;j++){//初始化
for(int i=1;i+(1<<j)-1<=2*n;i++){
st[i][j]=max(st[i][j-1],st[i+(1<<(j-1))][j-1]);
}
}
for(int i=1;i<=n;i++){
int ans=min((query(i+1,i+n/2)<a[i].b?0x3f3f3f3f:bs(i,i+1,i+n/2)),(query(i-1,i-n/2)<a[i].b?0x3f3f3f3f:rev_bs(i,i-n/2,i-1)));
//重点长难句 包括对区间里有没有解的预先判断,两个解取min等
cout<<(ans==0x3f3f3f3f?-1:ans)<<' ';//无解判断
}
}
0x32 Problem 2
link:P8818 [CSP-S 2022] 策略游戏 进行鞭尸
Solution:我觉得这道题应该不需要Solution了。
#include<bits/stdc++.h>
using namespace std;
int a_max[100005][17];
int a_min[100005][17];
int b_max[100005][17];
int b_min[100005][17];
int a_pos[100005][17];
int a_neg[100005][17];
int a[100005];
int b[100005];
int main(){
int n,m,q;
cin>>n>>m>>q;
for(int i=1;i<=n;i++){
cin>>a[i];
}
for(int i=1;i<=m;i++){
cin>>b[i];
}
for(int i=1;i<=n;i++){
a_max[i][0]=a[i];
a_min[i][0]=a[i];
if(a[i]>=0){
a_pos[i][0]=a[i];
}else{
a_pos[i][0]=0x3f3f3f3f;
}
if(a[i]<=0){
a_neg[i][0]=a[i];
}else{
a_neg[i][0]=-0x3f3f3f3f;
}
}
for(int i=1;i<=n;i++){
b_max[i][0]=b[i];
b_min[i][0]=b[i];
}
for(int j=1;j<=17;j++){
for(int i=1;i+(1<<j)-1<=n;i++){
a_max[i][j]=max(a_max[i][j-1],a_max[i+(1<<(j-1))][j-1]);
a_min[i][j]=min(a_min[i][j-1],a_min[i+(1<<(j-1))][j-1]);
b_max[i][j]=max(b_max[i][j-1],b_max[i+(1<<(j-1))][j-1]);
b_min[i][j]=min(b_min[i][j-1],b_min[i+(1<<(j-1))][j-1]);
a_pos[i][j]=min(a_pos[i][j-1],a_pos[i+(1<<(j-1))][j-1]);
a_neg[i][j]=max(a_neg[i][j-1],a_neg[i+(1<<(j-1))][j-1]);
}
}
#define int long long
for(int i=1;i<=q;i++){
int l1,r1,l2,r2;
cin>>l1>>r1>>l2>>r2;
int amax=max(a_max[l1][__lg(r1-l1+1)],a_max[r1-(1<<(__lg(r1-l1+1)))+1][__lg(r1-l1+1)]);
int amin=min(a_min[l1][__lg(r1-l1+1)],a_min[r1-(1<<(__lg(r1-l1+1)))+1][__lg(r1-l1+1)]);
int bmax=max(b_max[l2][__lg(r2-l2+1)],b_max[r2-(1<<(__lg(r2-l2+1)))+1][__lg(r2-l2+1)]);
int bmin=min(b_min[l2][__lg(r2-l2+1)],b_min[r2-(1<<(__lg(r2-l2+1)))+1][__lg(r2-l2+1)]);
int apos=min(a_pos[l1][__lg(r1-l1+1)],a_pos[r1-(1<<(__lg(r1-l1+1)))+1][__lg(r1-l1+1)]);
int aneg=max(a_neg[l1][__lg(r1-l1+1)],a_neg[r1-(1<<(__lg(r1-l1+1)))+1][__lg(r1-l1+1)]);
if(amin>=0&&bmin>=0){
cout<<amax*bmin<<endl;
continue;
}
if(amin>=0&&bmin<=0){
cout<<amin*bmin<<endl;
continue;
}
if(amax<=0&&bmax<=0){
cout<<amin*bmax<<endl;
continue;
}
if(amax<=0&&bmax>=0){
cout<<amax*bmax<<endl;
continue;
}
if(bmin>=0){
cout<<amax*bmin<<endl;
continue;
}
if(bmax<=0){
cout<<amin*bmax<<endl;
continue;
}
cout<<max(apos*bmin,aneg*bmax)<<endl;
continue;
}
}
0x33 Problem 3
link:P7974 [KSN2021] Delivering Balls 阴间的
不要看他的题面,翻译的很不好。 可以看这个。
Solution:实为阴间题。
我们把题目里面的蓝线叫做山(很形象对不对),起点设为\(l\),终点设为\(r\)。
首先我们先进行一个贪心:
-
绝不会出现掉头(往远离终点的方向走)的情况:显然。
-
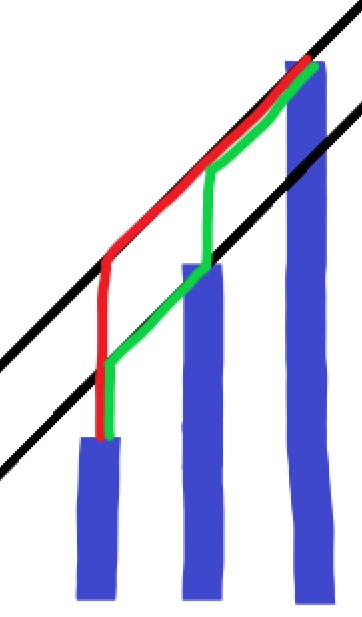
能斜着走就不直上直下:看图,黑字是每一段消耗的体力。
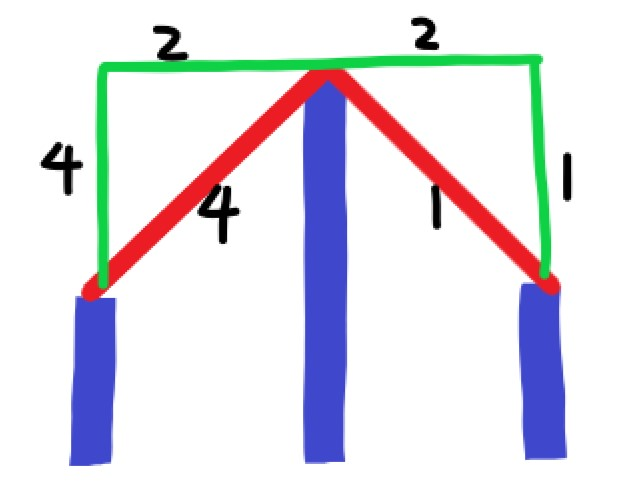
- 如图红线和绿线的花费是一样的,所以不如直接找到使得 \(H_i-H_{l}-(l-i)\) 最大的 \(i\) ,在 \(l\) 上原地升天 \(H_i-H_{l}-(l-i)\) 这么多。(不知道这个柿子是什么意思?就是相当于一个“经过 \(H_i\) 的斜率为1的直线(在图中用黑线表示)在 \(l\) 上的截距”,就是红线和绿线在起点直上直下的部分)。
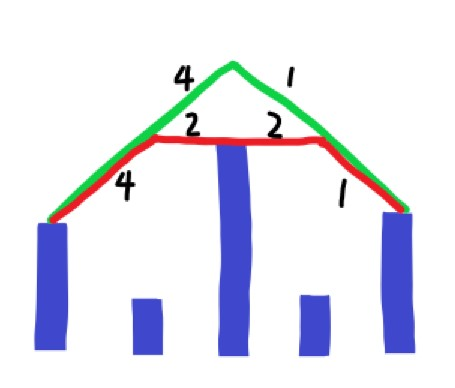
- 如图,绿线顶个尖尖出来完全没有必要,路径一定是尽可能地“平”。
经过这一番贪心,我们可以得出最终路径的大概模样:
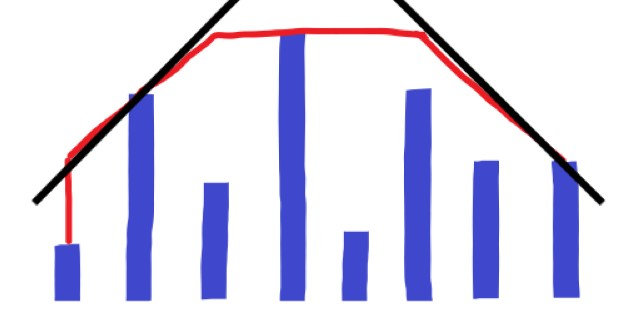
设“使得 \(H_i-H_{l}-(l-i)\) 最大的 \(i\) ”为 \(lhigh\) ,“使得 \(H_i-H_{r}-(i-r)\) 最大的 \(i\) ”为 \(rhigh\) 。
第一部分: \(l\) 到 \(lhigh\) 。(图中为 \(1\to2\) )
第二部分: \(lhigh\) 到 \(rhigh\) 。(图中为 \(2\to8\) )
第三部分: \(rhigh\) 到 \(r\) 。(图中为 \(8\to 8\) ,不存在)
我们算一下每一部分的体力消耗。
第一部分:显然就是 \(4(H_{lhigh}-H_l)\) (四倍高度差)。
第二部分:设 \([lhigh,rhigh]\) 中的最高峰为 \(nhigh\) 。
第二部分可以再分成三小段:上升段,平行段,下降段。
上升段为 \(4(H_{nhigh}-H_{lhigh})\) (也是四倍高度差)
下降段为 \(H_{nhigh}-H_{rhigh}\) (一倍高度差)
平行段为 \(2((rhigh-lhigh)-(H_{nhigh}-H_{lhigh})-(H_{nhigh}-H_{rhigh}))\) (总长度减去上升段和下降段就是平行段)
第三部分: \(H_{rhigh}-H_r\) (一倍高度差)
最后相加就是总体力消耗了。
下面,考虑一下 \(lhigh,rhigh,nhigh\) 怎么求。
\(nhigh\) 不必多说。ST表,在初始化的时候顺带维护最大值的位置即可。
至于 \(lhigh\) ,看一下定义: \(H_i-H_{l}-(l-i)\) 最大的 \(i\) 。 \(H_l\) 和 \(l\) 是定值,对于每个山都一样。把这两个东西从柿子里扔掉,我们发现,第 \(i\) 个山获得了 \(i\) 的加成。所以。对于所有 \(H_i\) ,我们直接把 \(H_i-=i\) ,此时 \(lhigh\) 就是区间 \([l,r]\) 的最大值。ST表维护。
\(rhigh\) 区别不大,改成 \(H_i-=(N-i+1)\) 即可。
最后,我们就完成了这道题。
还有一些细节:
-
有可能 \(l>r\) 。
swap一下然后把四倍高度差一倍高度差对调一下就行。 -
山的高度 \(<1e9\) ,会爆
int,开long long。
阴间代码警告!!
#include<bits/stdc++.h>
#define int long long
using namespace std;
struct ST{
int val;
int pos;//最大值的位置也需要维护
};
int a[200005];
int l_a[200005];
int r_a[200005];
ST st_l[200005][19];
ST st_r[200005][19];
ST st_n[200005][19];
signed main(){
int n,q;
cin>>n;
for(int i=1;i<=n;i++){
cin>>a[i];
}
for(int i=1;i<=n;i++){
l_a[i]=a[i]-i;//为了维护lhigh,处理原数据
r_a[i]=a[i]-(n-i+1);//rhigh
}
for(int i=1;i<=n;i++){
st_l[i][0].val=l_a[i];
st_r[i][0].val=r_a[i];
st_n[i][0].val=a[i];
st_l[i][0].pos=i;
st_r[i][0].pos=i;
st_n[i][0].pos=i;
}
for(int j=1;j<=19;j++){//大型初始化现场
for(int i=1;i+(1<<j)-1<=n;i++){
if(st_l[i][j-1].val>st_l[i+(1<<(j-1))][j-1].val){
st_l[i][j].val=st_l[i][j-1].val;
st_l[i][j].pos=st_l[i][j-1].pos;
}else{
st_l[i][j].val=st_l[i+(1<<(j-1))][j-1].val;
st_l[i][j].pos=st_l[i+(1<<(j-1))][j-1].pos;
}
if(st_r[i][j-1].val>st_r[i+(1<<(j-1))][j-1].val){
st_r[i][j].val=st_r[i][j-1].val;
st_r[i][j].pos=st_r[i][j-1].pos;
}else{
st_r[i][j].val=st_r[i+(1<<(j-1))][j-1].val;
st_r[i][j].pos=st_r[i+(1<<(j-1))][j-1].pos;
}
if(st_n[i][j-1].val>st_n[i+(1<<(j-1))][j-1].val){
st_n[i][j].val=st_n[i][j-1].val;
st_n[i][j].pos=st_n[i][j-1].pos;
}else{
st_n[i][j].val=st_n[i+(1<<(j-1))][j-1].val;
st_n[i][j].pos=st_n[i+(1<<(j-1))][j-1].pos;
}
}
}
cin>>q;
for(int i=1;i<=q;i++){
bool rev=false;
int l,r;
cin>>l>>r;
if(l>r){//如果l>r,交换,标记reverse用来调整体力倍率
rev=true;
swap(l,r);
}
ST lhigh=(st_l[l][__lg(r-l+1)].val>st_l[r-(1<<(__lg(r-l+1)))+1][__lg(r-l+1)].val?
st_l[l][__lg(r-l+1)]:st_l[r-(1<<(__lg(r-l+1)))+1][__lg(r-l+1)]);
ST rhigh=(st_r[l][__lg(r-l+1)].val>st_r[r-(1<<(__lg(r-l+1)))+1][__lg(r-l+1)].val?
st_r[l][__lg(r-l+1)]:st_r[r-(1<<(__lg(r-l+1)))+1][__lg(r-l+1)]);
ST nhigh=(st_n[l][__lg(r-l+1)].val>st_n[r-(1<<(__lg(r-l+1)))+1][__lg(r-l+1)].val?
st_n[l][__lg(r-l+1)]:st_n[r-(1<<(__lg(r-l+1)))+1][__lg(r-l+1)]);
//阴间的......
cout<<
(a[lhigh.pos]-a[l])*(rev?1:4)
+ (a[nhigh.pos]-a[lhigh.pos])*(rev?1:4)
+ (rhigh.pos-lhigh.pos-(a[nhigh.pos]-a[lhigh.pos])-(a[nhigh.pos]-a[rhigh.pos]))*2
+ (a[nhigh.pos]-a[rhigh.pos])*(rev?4:1)
+ (a[rhigh.pos]-a[r])*(rev?4:1)
<<endl;
}
}
闲话:其实这道题除了代码毒瘤一点还是很可以的,把题目中“行变换计算体力”改成“列变换计算体力”也能做思路差不多而且会简单很多(不要问我为什么知道 问就是读错题了...)。另外,用线段树做一个带修的版本也很好,甚至可以再加上山的删除(类似链表那种删除,删掉以后位置也被挤掉那种),用线段树应该也可以进行解决(没仔细想,应该没问题),再毒瘤一点可以再塞一个在末尾增加山,好像也能做......总之扩展一下还能玩出很多新花样,然后在毒瘤的路上越走越远[doge]
0x40 额外题单
P2880 [USACO07JAN] Balanced Lineup G:板子。
P7809 [JRKSJ R2] 01 序列:维护的东西很有意思


 浙公网安备 33010602011771号
浙公网安备 33010602011771号