题解：BLO-Blockade

本文仅发布于此博客和作者的洛谷博客，不允许任何人以任何形式转载，无论是否标明出处及作者。

---

柿子比较毒瘤（可能还是做的题有点少罢（

P3469 [POI2008]BLO-Blockade

题意

给你一张$n$个点，$m$条边的无向图，保证连通。

对于每一个节点$i$，请给出在图中删除和$i$相连的所有边后，不再连通的有序点对$(x,y)$的数量。

注意，删除边的操作是暂时的（就是删除和$i$相连的边时，之前删除的和$i-1$相连的边会恢复），且删除边的时候点会仍然保留。

思路

首先，连接一个点的所有边被删掉以后，图肯定会裂成几个连通块。设任意一个点$i$所在的连通块$P$里面的点的数量为$sum_P$，那么有几个点可以和$i$组成一个满足题目要求的有序对$(i,j)$呢？$(n-sum_P)$个。（$P$内的所有点都不能和$i$组成有序对,$P$以外的都可以）

$P$内总共有$sum_P$个点，每个点都有相同的$(n-sum_P)$个点可以组成有序对，整个连通块$P$的所有点和其他点可以组成的有序对数量就是$sum_P\times(n-sum_P)$，我们称这个数量为$P$的贡献。

显然，题目所求就是所有连通块的贡献之和。我们看一下整个图会裂成哪几种连通块。

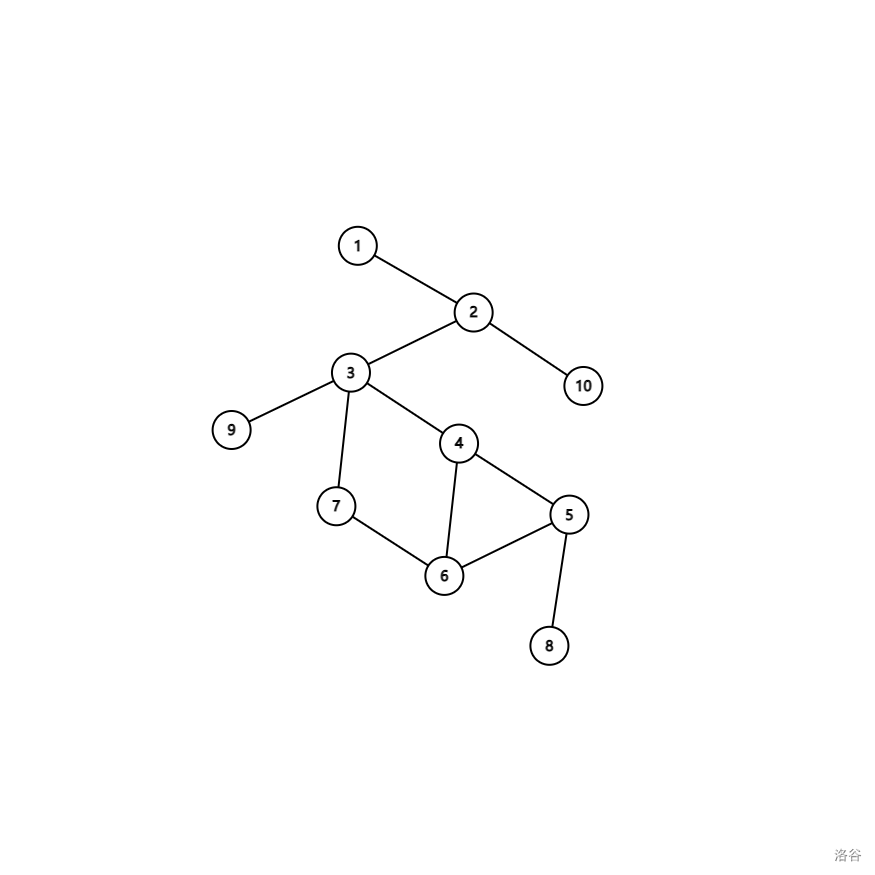
这是一个图，我们把和3相连的边去掉

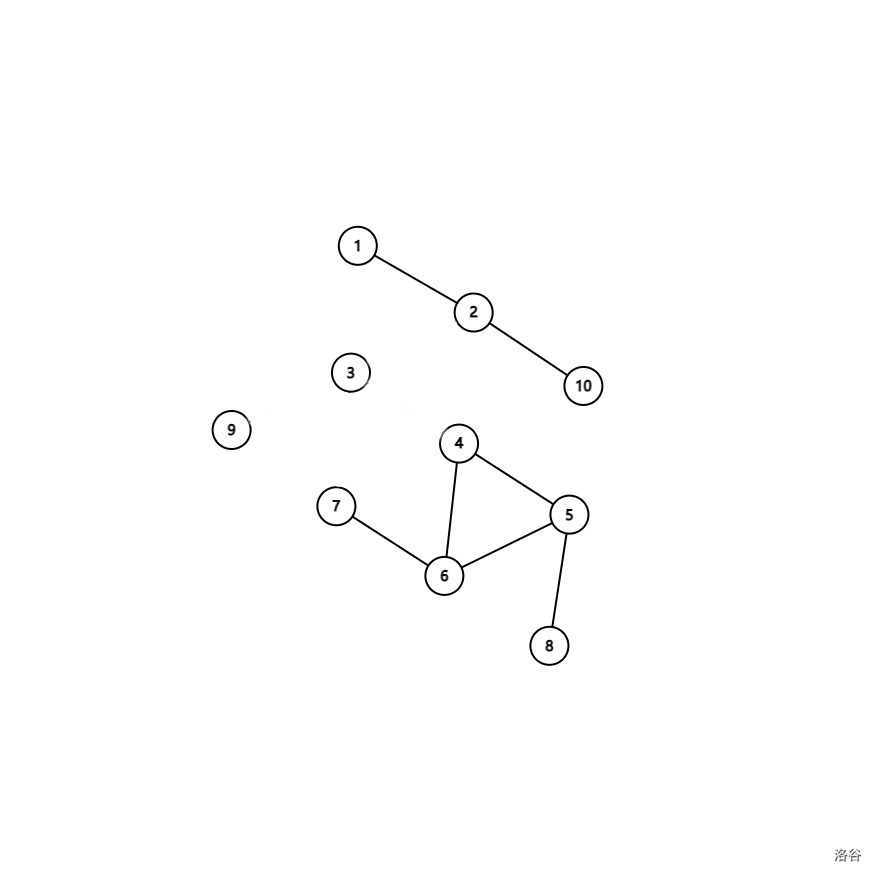
发现，裂成的连通块总共有三种：

1. 主体部分（1,2,10）

2. (没有连接到主体部分上的) 以3的儿子为根的子树（9）和（4,5,6,7,8）

3. 3本身（3）

我们发现，一个图在删掉所有连接点$i$的边后，会分裂成$k+2$块。

$k$块“子树”，$1$块“$i$”，$1$块“主体”.

对于$k$块“子树”,它们的贡献之和是$\sum\limits_{j=1}^{k} sum_j(n-sum_j)$。

对于“$i$”，贡献是$1\times(n-1)$。

因为“主体”是原图的所有节点刨去“子树”和“$i$”的部分，剩余下来的，所以“主体”的节点数为$n-\sum\limits_{j=1}^k sum_j-1$。

所以对于“主体”,贡献是$(n-\sum\limits_{j=1}^k sum_j-1)(\sum\limits_{j=1}^k sum_j+1)$.

于是，我们就可以得到删除和$i$相连的所有边后，不再连通的有序点对$(x,y)$的数量：

$$(n-\sum_{j=1}^k sum_j-1)(\sum_{j=1}^k sum_j+1)+\sum_{j=1}^ksum_j(n-sum_j)+(n-1)$$

好的，那我们的柿子就推到这里就可以了。

那么我们就需要求出来删掉点$i$后，每个没有和主体连接的，以$i$的儿子为根的子树的大小。

考虑使用Tarjan算法，在求割点的代码基础上作一点改造。

分成两部分，一部分找到子树，一部分计算子树的大小。

先看第一部分。

在判定割点的时候，如果low[g[k][i]]>=dfn[k]，就代表以g[k][i]这个儿子为根的子树没有连接上主体。

此时，我们记录g[k][i]，就找到了一个没连接上主体的子树。

而第二部分可以在dfs中顺带实现，计算以所有点为根的子树大小不难。

和割点不同的是，在dfs根节点的时候，完全不需要进行额外的处理。

处理根节点时，我们把主体看成$0$个点，显然所有子树都与其不连通。这时，可以直接套用柿子不会出错。

$$\Huge\textit{Talk is cheap. Show me the code.}$$

#include<bits/stdc++.h>
#define int long long//十年OI一场空，不开long long见祖宗！！1
using namespace std;
int n,m;
vector<int> g[100005];
int dfn[100005];
int low[100005];
int fa[100005];
int subtree[100005];//一个点的子树大小
int sum[100005];//就是题目要求求的那个有序对数量了
int cnt=0;
void calc(int k,vector<int> child){
	int remains=n;//主体中点的数量
	remains--;//k自己是一个连通块，不在主体中
	for(int i=0;i<child.size();i++){	
		remains-=subtree[child[i]];//没连上主体的子树，不在主体中。
	}
	sum[k]+=remains*(n-remains);//主体计数
	for(int i=0;i<child.size();i++){
		sum[k]+=subtree[child[i]]*(n-subtree[child[i]]);//没连上主体的子树计数
	}
	sum[k]+=1*(n-1);//k自己计数
}
void tarjan(int k){//注意这里没有了root
	vector<int> child;//存储没连上主体的子树
	child.clear();
	cnt++;
	dfn[k]=cnt;
	low[k]=cnt;
	subtree[k]=1;//子树大小。先算上自己。
	for(int i=0;i<g[k].size();i++){
		if(g[k][i]==fa[k]){//如果是父亲节点就不搜
			continue;
		}
		if(dfn[g[k][i]]==0){
			fa[g[k][i]]=k;
			tarjan(g[k][i]);
			low[k]=min(low[k],low[g[k][i]]);//Tarjan标准操作 更新low值
			subtree[k]+=subtree[g[k][i]];//子树大小更新。
			if(low[g[k][i]]>=dfn[k]){//这里是发现一个没连上主体的子树
				child.push_back(g[k][i]);//记录一下，等着一起扔进柿子里算。
			}
		}else{
			low[k]=min(low[k],dfn[g[k][i]]);//Tarjan标准操作*2
		}
	}
	calc(k,child);//把子树什么的扔进柿子里算就完了
}
signed main(){
	int tmpa,tmpb;
	cin>>n>>m;
	for(int i=1;i<=m;i++){
		cin>>tmpa>>tmpb;
		g[tmpa].push_back(tmpb);
		g[tmpb].push_back(tmpa);
	}
	tarjan(1);//无向图本身连通，随便一个节点开始dfs就好
	for(int i=1;i<=n;i++){
		cout<<sum[i]<<endl;
	}
}

圆满！