szkzyc小组抛物线与光学作业。
本文仅发布于此博客和作者的洛谷博客,不允许任何人以任何形式转载,无论是否标明出处及作者。
Part 1
Problem 1
给出二次函数\(y=x^2\)对应的抛物线的焦点坐标与准线方程。
\[\begin{aligned}
&\because \text{焦点在对称轴上,准线}\perp\text{对称轴,对称轴为}x=0\\
&\therefore \text{设焦点为}(0,m),\text{准线为}y=n.\\
&\text{由定义,}\sqrt{(-x)^2+(m-x^2)^2}=|x^2-n|\text{对于任意}x\text{均成立。}\\
&\text{分别代入}x=0,x=1,\text{得到}\\
&\begin{cases}
m^2=n^2\\
m^2-n^2-2m+2n+1=0
\end{cases}\\
&\text{解得}\begin{cases}
m=\frac{1}{4}\\
n=-\frac{1}{4}
\end{cases}\\
\\
&\therefore\text{焦点}(0,\frac{1}{4}),\text{准线}y=-\frac{1}{4}.
\end{aligned}\]
Problem 2
给出二次函数\(y=ax^2(a\neq 0)\)对应的抛物线的焦点坐标与准线方程。
\[\begin{aligned}
&\therefore \text{仍设焦点为}(0,m),\text{准线为}y=n.\\
&\sqrt{(-x)^2+(m-ax^2)^2}=|ax^2-n|\text{对于任意}x\text{均成立。}\\
&\text{代入}x=0,x=1,\text{得到}\\
&\begin{cases}
m^2=n^2\\
m^2-n^2-2am+2an+1=0
\end{cases}\\
&\text{解得}\begin{cases}
m=\frac{1}{4a}\\
n=-\frac{1}{4a}
\end{cases}\\
\\
&\therefore\text{焦点}(0,\frac{1}{4a}),\text{准线}y=-\frac{1}{4a}.
\end{aligned}\]
Problem 3
给出二次函数\(y=x^2+4x+3\)对应的抛物线的焦点坐标与准线方程。
\[\begin{aligned}
&\because \text{焦点在对称轴上,准线}\perp\text{对称轴,对称轴为}x=-2\\
&\therefore \text{设焦点为}(-2,m),\text{准线为}y=n.\\
&\sqrt{(x+2)^2+(x^2+4x+3-m)^2}=|x^2+4x+3-n|\text{对于任意}x\text{均成立。}\\
&\text{分别代入}x=-2,x=-1,\text{得到}\\
&\begin{cases}
(m+1)^2=(n+1)^2\\
m^2+1=n^2
\end{cases}\\
&\text{解得}\begin{cases}
m=-\frac{3}{4}\\
n=-\frac{5}{4}
\end{cases}\\
\\
&\therefore\text{焦点}(-2,-\frac{3}{4}),\text{准线}y=-\frac{5}{4}.
\end{aligned}\]
Part 2
Problem 4
求\(y=2x^2\)在\(P(1,2)\)处的切线方程。
\[\begin{aligned}
&\text{设切线为}k(x-1)+2,\text{则}\\
&2x^2=k(x-1)+2\text{的}\Delta=0\\
&\text{即}k^2-8k+16=0,\text{解得}k=4.\\
&\therefore\text{切线方程为}y=4x-2.
\end{aligned}
\]
Problem 5
求\(y=x^2+2x-5\)在\(P(3,10)\)处的切线方程。
\[\begin{aligned}
&\text{设切线为}k(x-3)+10,\text{则}\\
&x^2+2x-5=k(x-3)+10\text{的}\Delta=0\\
&\text{即}k^2-16k+64=0,\text{解得}k=8.\\
&\therefore\text{切线方程为}y=8x-14.
\end{aligned}
\]
Problem 6
求过点\(P(3,9)\),且与\(y=x^2+2x-5\)相切的直线方程。
\[\begin{aligned}
&\text{设切线为}k(x-3)+9,\text{则}\\
&x^2+2x-5=k(x-3)+9\text{的}\Delta=0\\
&\text{即}k^2-16k+60=0,\text{解得}k=10\text{或}6.\\
&\therefore\text{切线方程为}y=10x-21\text{或}y=6x-9.
\end{aligned}
\]
Problem 7
设点\(P\)在抛物线上,过点\(P\)的切线交准线于\(Z\),设抛物线焦点为\(F\),证明:\(\angle PFZ=90^{\circ}\)
\[\begin{aligned}
&\text{设抛物线为}y=ax^2(a\neq 0),\text{则焦点为}F(0,\frac{1}{4a}),\text{准线为}y=-\frac{1}{4a}.\\
&\text{设切线切抛物线于}P(m,am^2),\text{则切线方程为}2amx-am^2.\\
&\text{切线交准线于}Z(-\frac{1}{8a^2m}+\frac{1}{2}m,-\frac{1}{4a}).\\
\\
&\text{当}am^2\neq \frac{1}{4a}\text{时,}\\
&PF\text{的斜率为}am-\frac{1}{4am},FZ\text{的斜率为}\frac{4am}{1-4a^2m^2}.\\
&\because am-\frac{1}{4am}\times\frac{4am}{1-4a^2m^2}=-1\\
&\therefore PF\perp FZ.\\
&\therefore \angle PFZ=90^{\circ}.\\
\\
&\text{当}am^2=\frac{1}{4a}\text{时,}\\
&\text{切线方程为}\pm x-\frac{1}{4a},\text{交准线于}(0,-\frac{1}{4a}).\\
&\text{此时}PF\perp x\text{轴},FZ\text{在}y\text{轴上},PF\perp FZ.\\
&\therefore \angle PFZ=90^{\circ}.
\end{aligned}
\]
Problem 8
设\(A\),\(B\)为抛物线的焦点弦,过\(A\),\(B\)分别做抛物线的两条切线,
证明:这两条切线互相垂直,且交点在准线上。
不会。
Part 3
Problem 9
根据费马原理解释光入射平面镜时的反射规律。
\[\begin{aligned}
&\text{根据物理常识,平面镜成像,像距=物距}\\
&\therefore\text{平面镜成像的光线可以看作从像射出。}\\
&\because\text{费马原理,光线走最短路。}\\
&\therefore\text{从像距射出的光线是一条直线。}
\end{aligned}
\]
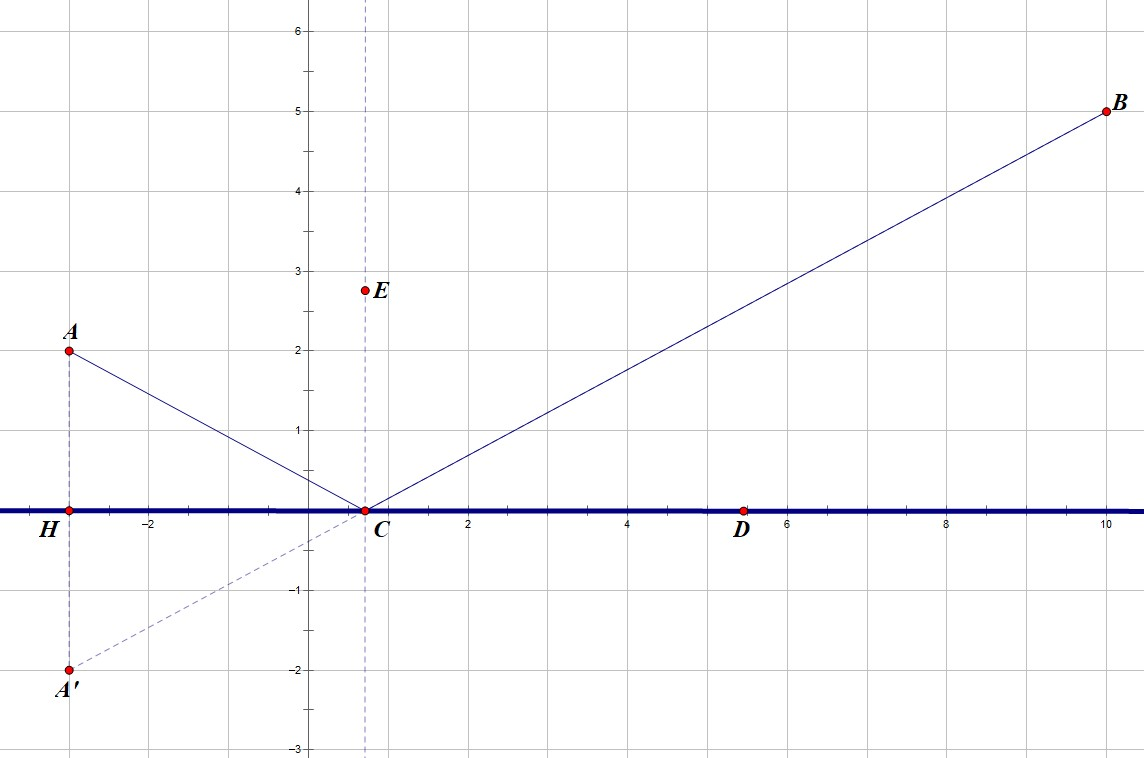
\[\begin{aligned}
&\because\text{在}\triangle AHC\text{和}\triangle A'HC\text{中},\\
&\begin{cases}
AH=A'H(\text{像距=物距})\\
\angle AHC=\angle A'HC=90^{\circ}\\
HC=HC
\end{cases}\\
&\therefore \triangle AHC\cong\triangle A'HC(SAS)\\
&\therefore \angle ACH=\angle A'CH=\angle BCD.\\
&\therefore \angle ACE=\angle BCE.\\
&\therefore \text{反射角=入射角.}
\end{aligned}
\]
Problem 10
当光入射抛物线形镜面时,设入射点为\(P\),则入射光线、出射光线与点\(P\)处的切线夹角相等,试用费马原理进行解释。
暂时不会。
Part 4
Problem 11
设抛物线方程为\(y=ax^2\),证明它的光学性质。
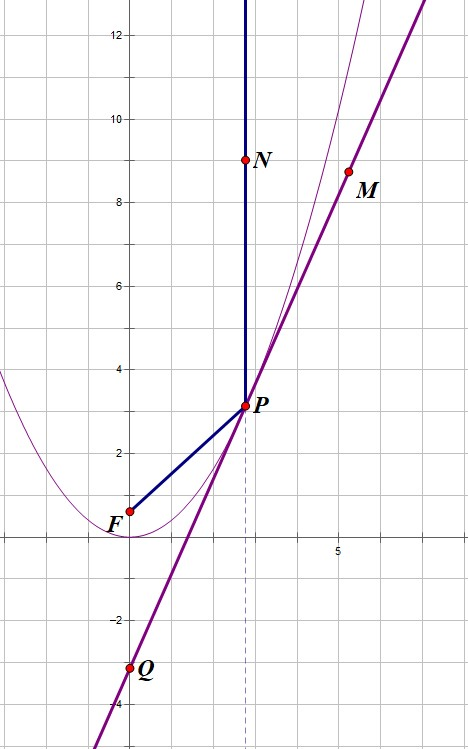
\[\begin{aligned}
&\text{从焦点}F\text{射出的光线在}P\text{反射,切线}MQ\text{切抛物线于}P,\text{交}y\text{轴于Q}.\text{证明反射光线}PN//y\text{轴}.\\
&\because\text{费马定理,}\angle MPN=\angle QPF.\\
&\text{若}\angle PQF=\angle MPN,\text{即}\angle PQF=\angle QPF,\text{则}PN//y\text{轴},\text{即可得证}.\\
&\because\text{当}\angle PQF=\angle QPF\text{时},\triangle FPQ\text{等腰,}\\
&\therefore \text{即证}PF=FQ.\\
\\
&\text{设}P(m,am^2),\text{易得切线}MQ:y=2amx-am^2.\\
&\therefore Q(0,-am^2).\\
&\text{易得}F(0,\frac{1}{4a}).\\
&PF=\sqrt{(m-0)^2+(am^2-\frac{1}{4a})^2}=\sqrt{a^2m^4+\frac{1}{16a^2}+\frac{1}{2}m^2}.\\
&FQ=\sqrt{(\frac{1}{4a}+am^2)^2}=\sqrt{a^2m^4+\frac{1}{16a^2}+\frac{1}{2}m^2}.\\
&\therefore PF=FQ.\\
&\therefore \text{得证}.
\end{aligned}
\]
Problem 12
不建立坐标系,只根据抛物线的定义及性质,用几何方法证明抛物线的光学性质。
不会。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号