彻底弄懂B树、B+树

平衡二叉树

• 概念：平衡二叉树是基于二分法的策略提高数据的查找速度的二叉树的数据结构

• 特点：（1）非叶子节点只能允许最多两个子节点存在 　　（2）每一个非叶子节点数据分布规则为左边的子节点小当前节点的值，右边的子节点大于当前节点的值

 

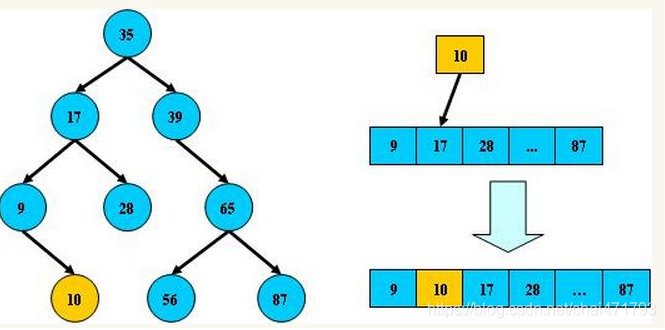
平衡树的层级结构：因为平衡二叉树查询性能和树的层级（h高度）成反比，h值越小查询越快、为了保证树的结构左右两端数据大致平衡降低二叉树的查询难度一般会采用一种算法机制实现节点数据结构的平衡，

实现了这种算法的有比如Treap、红黑树，使用平衡二叉树能保证数据的左右两边的节点层级相差不会大于1，

通过这样避免树形结构由于删除增加变成线性链表影响查询效率，保证数据平衡的情况下查找数据的速度近于二分法查找

 

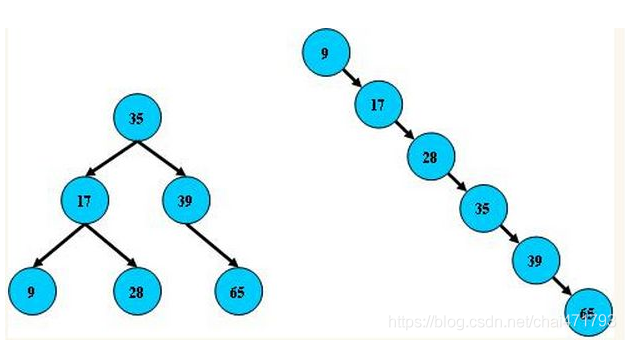
总结平衡二叉树特点：
（1）非叶子节点最多拥有两个子节点；
（2）非叶子节值大于左边子节点、小于右边子节点；
（3）树的左右两边的层级数相差不会大于1;
（4）没有值相等重复的节点;

 

 

 2-3树

2-3树是一种多路查找树：2和3的意思是2-3树包含两种节点

• 2节点包含一个元素和两个孩子（或者没有孩子）
  • 左子树包含节点的元素值小于该节点的元素值，右子树包含的节点的元素值大于该节点的元素值
  • 2节点要么有两个孩子，要么就没有孩子，不允许只有一个孩子　
• 3节点包含一大一小两个元素和三个孩子（或者没有孩子），（两个元素按从小到大排列好）
  • 左子树包含的节点的元素值小于该节点较小的元素值，右子树包含的节点的元素值大于该节点较大的元素值，中间子树包含的节点的元素值介于这两个元素之间
  • 3节点要不有三个孩子，要不就没有孩子，不允许有一个孩子或两个孩子
• 2-3树所有叶子节点都在同一层次

 

 

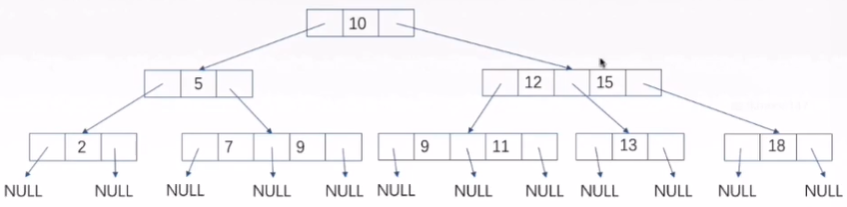
B树

B树也是一种平衡的多路查找树，2-3树是B树的特例，我们把树中节点最大的孩子数目称为B树的阶，通常记为m

举个例子：2-3树种的3节点，所以2-3树的阶m=3

B树的特点如下： 

• 树种每个节点至多有m颗子树（即至多含有m-1个关键字）（两颗子树指针夹着一个关键字）
• 若根节点不是终端节点，则至少有两颗子树（至少一个关键字）
• 除根节点外的所有非叶子节点至少有【m/2】颗子树（即至少含有【m/2】-1个关键字）
• 所有叶子节点出现在同一层次上，不带信息
• 所有非叶子节点的结构如下

B树的查找操作

B树是多路查找树，二叉排序树是二路查找，B树是多路查找，所以它是二叉排序树的扩展，查询方式十分类似

查找过程

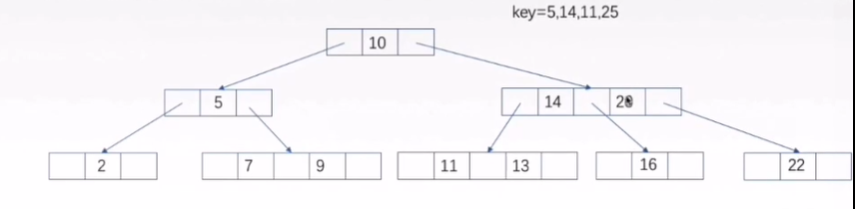
• 先让待查找关键字key和节点中的关键字比较，如果等于其中某个关键字，则查找成功
• 如果和所有关键字都不相等，则看key处于哪个范围内，然后去对应的指针所指向的子树中查找

举个例子：如果key比第一个关键字K1还小，则去P0指针所指向的子树中查找，如果比最后一个关键字Kn还大，则去Pn指针所指向的子树中查找