前缀和

再 Range Queries 问题中，有这样一个经典操作：

\(\operatorname{sum}_q(a,b)\)：区间 \([a,b]\) 的所有值的和。

对于 Static Range Queries（没有修改操作），我们可以进行 \(O(n)\) 的预处理后 \(O(1)\) 地做到每次查询，方法也不难，只需要前缀和即可。

一维前缀和

首先，那么对于任意区间 \([l,r]\) 和任意下标 \(id\)，其中 \(1\leq id\leq l\leq r\leq n\)，都有 \(\operatorname{sum}_q(l,r)=\operatorname{sum}_q(id,r)-\operatorname{sum}_q(id,l-1)\)。
因此，大致思路就是令 \(q_i=\operatorname{sum}_q(1,i)\)，那么 \(\operatorname{sum}_q(l,r)=q_r-q_{l-1}\)。

所谓“前缀和”，就是预处理好任意前缀的和，即把每个 \(\operatorname{sum}_q(1,i)\) 都提前计算好存下来。

int q[N],a[N];
void init(int n) {
    q[0]=0;
    for(int i=1;i<=n;++i) q[i]=q[i-1]+a[i];
}
int query(int l,int r) {
    return q[r]-q[l-1];
}

代码大致就是如此，比较简单。

二位前缀和

在二维空间（二维数组）里，我们也可以进行前缀和操作，而二位前缀和实质就是一种容斥的应用。

预处理

我们令 \(q_{i,j}\) 表示前 \(i\) 行 \(j\) 列的数字的总和，然后考虑如何初始化：

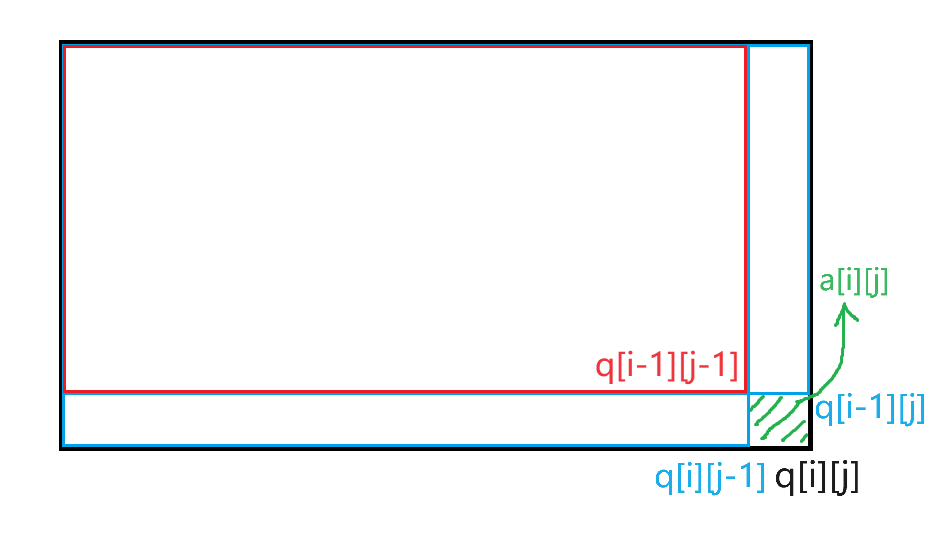
用几何的角度思考，黑色大长方形的面积就可以用两个蓝色长方形的面积和减红色长方形再加绿色长方形的面积来表示，形象地说就是：\(S_{black}=S_{blue1}+S_{blue2}-S_{red}+S_{green}\)，把这些长方形的面积换成字母，就有：\(q_{i,j}=q_{i-1,j}+q_{i,j-1}-q_{i-1,j-1}+a_{i,j}\)。

查询

那么，如何查询一个以 \((x_1,y_1)\) 为左上角，\((x_2,y_2)\) 为右下角的长方形中的数字和呢？也就是，如何用前缀和来表示任意面积呢？

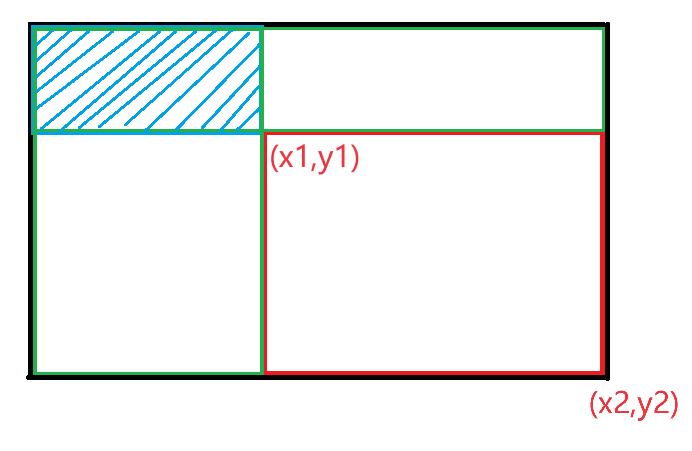
还是从几何意义去思考，以 \((x_1,y_1)\) 为左上角，\((x_2,y_2)\) 为右下角的红色长方形的面积就等于整个黑色长方形面积减去两个绿色长方形面积，再加上蓝色长方形的面积，就是：\(S_{red}=S_{black}-S_{green1}-S_{green2}+S_{blue}\)，把这些长方形的面积换成字母，就有：\(ans=q_{x_2,y_2}-q_{x_1-1,y2}-q_{x_2,y_1-1}+q_{x_1-1,y_1-1}\)。

代码

代码大致如下：

// 注意 y1 是 cmath 库里的函数，如果开了万能头或者引用了 cmath，就需要换一个变量名
int q[N][N],a[N][N];
void init(int n,int m) {
    for(int i=1;i<=n;++i)
        for(int j=1;j<=m;++j)
            q[i][j]=q[i][j-1]+q[i-1][j]-q[i-1][j-1]+a[i][j];
}
inline int query(int x1,int y1,int x2,int y2) {
    return q[x2][y2]-q[x1-1][y2]-q[x2][y1-1]+q[x1-1][y1-1];
}