KMP

KMP 算法是一种改进的字符串匹配算法，由 D.E.Knuth，J.H.Morris 和 V.R.Pratt 提出，以三个人名的首字母按字典序排列，将这个算法命名为 KMP 算法。

字符串匹配

现在给定长度为 \(n\) 的字符串 \(s\) 和长度为 \(m\) 的字符串 \(t\)，要求找到 \(t\) 在 \(s\) 中所有匹配的位置，即找到 \(s\) 的哪些子串与 \(t\) 完全相同。

考虑如果数据范围是 \(n,m\leq 10^4\)，那么这个问题会变的很容易，字符串匹配问题的这个版本可能在学习基础语法的时候就可能遇到过了，写法也很简单，大致如下：

void match(string s,string t) {
	for(int i=0;i+t.size()-1<s.size();++i) {
		bool flag=true;
		for(int j=0;j<t.size();++j) {
			if(s[i+j-1]!=t[j]) {
				flag=false;
				break;
			}
		}
		if(flag) cout<<i<<' '<<i+t.size()-1<<'\n';
	}
}

这样做的最坏时间复杂度是 \(O(nm)\) 的，虽然有了 break 语句之后在大部分时间都达不到，不过还是可以构造 hack，比如字符串 \(s\) 为 \(10000\) 个字母 A，字符串 \(t\) 为 \(5000\) 个字母 A，这样的话我们的上述代码会匹配 \(5000\times 5001=2.5\times 10^7\) 次。

那么，假如 \(n,m\leq 5\times 10^5\)，这种算法就很容易超时了，不过，对于这个数据范围，是否可解呢？

答案依旧是肯定的，在这个数据范围下，字符串匹配问题的稳定解法就是 KMP（当然，使用 hash 也是一种做法，不过可能出现 hash 冲突，所以不稳定）。
PS：当然你可以像傻子一样搞一个 AC 自动机，多此一举，不过其实 AC 自动机就基于 trie 树上的 kmp。

KMP 算法

优化暴力

可以发现，在刚才的暴力算法中，我们的做法是每次失配（不匹配）的时候，就直接 break，然后对于下一个位置，直接从头开始重新匹配，但是这样做实际是不好的，因为我们没必要这样做。

考虑刚才的匹配方法是有重复方案的，手动模拟可以发现，有的位置的匹配重复了，而有的位置没必要的匹配却进行了很多次。

考虑对于每个 \(s\) 串中的位置推进 \(t\) 串的位置，即将 \(i\) 作为结尾位置，而非将 \(s\) 串的第 \(i\) 个字符作为开始进行匹配，贪心地，对于 \(s\) 串的第 \(i\) 个位置尽可能最大长度的去和 \(t\) 匹配，用形象的语言来说的话，就是对于 \(s\) 串的第 \(i\) 个位置，找到最长的 \(l\)，使得 \(S_{i-l+1}S_{i-l+2}\dots S_{i-1}S_i=T_1T_2\dots T_{l-1}T_l\)。

这个状态可以考虑从 \(i-1\) 来转移，加入我们知道对于 \(i-1\) 最大匹配长度为 \(len\)，可以分这两种情况：

1. 先考虑最简单的情况：\(T_{len+1}=S_i\)，这样的话，对于 \(i\) 位置的最长匹配 \(l\) 就为 \(len+1\) 了
2. \(T_{len+1}\neq S_i\)，这样的话，我们就出现了失配的情况，失配时我们要考虑 \(l\) 应该重新设为多少，那么，这个操作是如何进行的呢，且看下面这张图片：

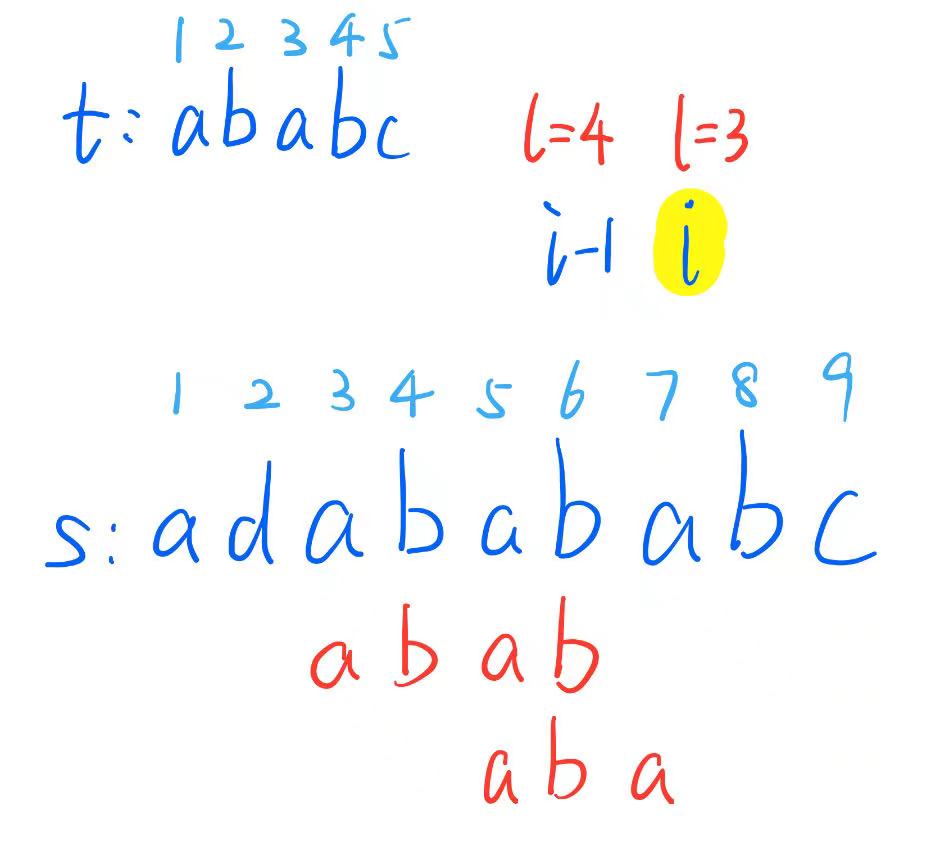
不妨用 \(i=7\) 作为一个例子，当匹配到 \(i-1\) 位置的时候，显然 \(l=4\)，即 \(t\) 串的 \([1,4]\) 与 \(s\) 串的 \([3,6]\) 可以完全匹配，不过此时，\(s_7\neq t_5\)，匹配失败，\(l\) 不能再变成 \(l+1\) 了，我们需要寻找新的 \(l\)，满足 \(t_1\dots t_l=s_{i-l+1}\dots s_i\)。

上述条件可以拆分：\(t_1\dots t_l=s_{i-l+1}\dots s_i \iff t_1\dots t_{l-1}=s_{i-l+1}\dots s_{i-1}\ \text{and}\ t_l=s_i\)，我们可以尝试找到满足 \(t_1\dots t_{l-1}=s_{i-l+1}\dots s_{i-1}\) 的 \(l\)，然后再判断 \(t_l=s_i\) 的真假性。

首先，一定有新的 \(l<len+1\)（\(len\) 为 \(i-1\) 位置的 \(l\) 值），由于对于 \(i-1\) 位置，满足 \(t_1\dots t_{len}=s_{i-len}\dots s_{i-1}\)，很自然的想到转化条件，进行等量代换，可知：有 \(t_1\dots t_{l-1}=s_{i-l+1}\dots s_{i-1}=t_{len-l+1}\dots t_{len}\)，那么这说明了什么，在已知 \(len\) 的情况下，求解新的可能的 \(l\) 是不需要 \(s\) 串的参与的，只需要看 \(t_1\dots t_{l-1}=t_{len-l+1}\dots t_{len}\) 的真假性即可，这个式子的直观含义如果能够被搞明白，那么求可能的 \(l\) 这个事情就变简单了。

这个式子的直观意义其实也是很简单的，就是指，对于 t 串的 substring \(t'=t_1\dots t_{len}\)，\(l\) 就是最长的长度，满足 \(t'\) 长度为 \(l<len\) 的前缀与长度为 \(l\) 的后缀相等，对于任意的 \(len\)，我们只要处理出这个值就可以了，我们把这个值预处理出来，用 \(next_i\) 表示当 \(len=i\) 时 \(t_1\dots t_i\) 的最长的前后缀匹配即可，然后当出现上述的适配情况的时候，如果刚才匹配了 \(len\)，那么如果匹配（\(s_i=t_{len+1}\)），则 \(len=len+1\)，否则 \(len=next_{len}\)，直到 \(len=0\) 或 \(s_i=t_{len+1}\) 为止，如果 \(s_i=t_{len+1}\)，还是需要 \(len=len+1\)，否则 \(len=0\) 表示对于 \(i\) 位置，一个字符都匹配不了。

那么，接下来又做的就是求解 \(next\) 数组，\(next\) 数组实际就是 \(t\) 串和自己跑 KMP，可以这样理解，如果一个前缀和一个后缀匹配，则这个后缀的一个后缀也一定可以找到这个前缀的一个前缀和它匹配。

correctness

证明这个算法是正确，只要证我们保证了每次的 \(len\) 都是对于每个位置的最长匹配长度，这样的话，就可以证明了，这个证明是简单的，从略。

efficiency

KMP 时间复杂度为 \(O(n+m)\)，可以感性地证明一下，首先在 \(t\) 和 \(s\) 串上各跑一次，分别是 \(O(m)\) 和 \(O(n)\)，其次，分别最多跳 \(next\) 数组 \(m\) 次和 \(n\) 次，也是 \(O(m)\) 和 \(O(n)\)，加在一起就是 \(O(2n+2m)\)，时间复杂度忽略常数，所以为 \(O(n+m)\)。

代码

#include<bits/stdc++.h>
using namespace std;
const int N = 1e6+5;
int nxt[N];
int main() {
	string s,t;
	cin>>s>>t;
	int n=s.size(),m=t.size();
	s=" "+s,t=" "+t;
	int len=0; //初始化一下 len=0
	for(int i=2;i<=m;++i) {
		while(t[i]!=t[len+1]&&len) len=nxt[len];
		// 如果不能匹配且 len!=0，那么就跳 nxt 数组寻找匹配
		if(t[i]==t[len+1]) len++;
		// 如果可以匹配，那么 len++
		nxt[i]=len;
		// 设置 nxt[i] 的值为当前的 len
	}
	// t 和 t 自己匹配建好 nxt 数组之后，就可以去和 s 匹配了
	len=0; //重新初始化
	for(int i=1;i<=n;++i) {
		while(s[i]!=t[len+1]&&len) len=nxt[len];
		// 同理的，如果不能匹配且 len!=0，跳 nxt 数组
		if(s[i]==t[len+1]) len++;
		// 如果可以匹配，还是 len++
		if(len==m) {
			// 如果匹配了 m 个字符，说明当前位置 i 可以和整个 t 串匹配
			cout<<i-len+1<<' '<<i<<'\n';
			// 输出答案
			len=nxt[len];
			// 这里要注意让 len=nxt[len]，因为如果 len 再加一的话就越界了
		}
	}
	return 0;
}