数据结构 - trie树

trie树

一.Trie的概念

Trie又称字典树，前缀树（事实上前缀树这个名字就很好的解释了Trie的储存方式）

trie 字典树是一种非常简单的数据结构。

来一张图理解一下Trie的储存方式：(图片来自百度百科)

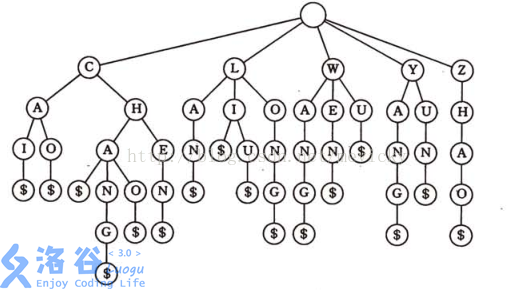
本图片来自 https://www.luogu.com.cn/blog/Ervin311/solution-p3879 ，如有侵权，请及时联系。

由这张图我们也可以知道Trie的特点：

Trie的根节点是空的。 除根节点外，每个节点储存一个单词/字母。 也就是说，从根节点到每个单词节点的路径上的所有字母连接而成的字符串就是该节点对应的字符串。 每个非叶子结点一般都会被多次使用，以节省遍历时的时间效率。 另外，每个节点下面的数字是他们的编号，这个具体在下面再展开。

我们把 26 个字母用 0−25 这 26 个数字表示，建立一棵树，如果一个节点上有一个表示从根到这个节点路径上的字母组成的字符串是存在的标记，那么从根到这个节点的路径组成的字符串是存在的，每次添加一个字符串，如果这个字符串的当前位置 trie 树里面有的话，那么就往这个节点走，否则建立这个节点，添加这个字符串结尾时，我们需要打上表示从根到这个节点路径上的字母组成的字符串是存在的标记。

所以读者们不难看出，

Trie是典型的用空间来换时间的做法

二.Trie的操作

Trie的常用操作：插入，查询，删除

1.插入（查询为常用操作，删除操作实在少见就不展开讲了）

在这之前我们需要填一下上面的坑：

那些非根节点下面的数字是什么意思？

事实上，在代码中，我们一般把根节点编号为 0 ，然后把其余节点从 1 开始编号，然后存在一个数组中（数组的用处是储存每个节点的所有子节点，以便于直接使用下标来存取）

再具体一点，在我的代码中，用 ch[i][j] 来保存i的那个编号为j的子节点，当然，如果 ch[i][j]==0，也就代表这个节点不存在，即i没有这个编号为j的子节点

好了，坑填完了

我们来明确一下另外一个数组的概念：val数组

对于需要用到Trie的题目，一般是不会只让你单纯构建一棵Trie的，一般都会有各种奇奇怪怪的要求，就像我们的例题（例题在下面），怎么处理这一些要求？我们可以把他们看作是一些“附加信息”，然后储存起来，val数组就是用来储存附加信息的

那么现在我们就来讲一下插入操作（具体解释都在代码中）:

（我的代码一般是没有指针这种不是很友好的东西的，不过这里因为是定义在结构体里面的，比较麻烦，所以干脆写个指针，意思很好懂的，代码中有注解）

#define ll int
#define N 500010 
struct Trie{
    ll ch[N][26],sz,val[N];
    //val为附加信息
    //这里的ch数组，第二维的大小为26是因为字符串只由小写字母构成，第二维的大小一般是由字符串的组成决定
    //sz即为节点编号 
    Trie(){
        sz=1;//一开始的时候只有根节点这一个节点 
        memset(ch[0],0,sizeof(ch[0]));
        memset(val,0,sizeof(val));
    }//这里是初始化 
    ll idx(char c){return c-'a';}//返回字符c的编号 
    void insert(char *s,ll v){
    //插入操作 ,这里是整份代码中唯一用到指针的地方，因为函数是放在结构体里面 ，所以最好用个指针，其实等价于char s[] 
    //s代表要插入的字符串，v为附加信息 
        ll u=0,len=strlen(s+1);
        for(ll i=1;i<=len;i++){
            ll c=idx(s[i]);
            if(!ch[u][c]){//如果节点不存在就插入，不然就继续往下遍历 
                memset(ch[sz],0,sizeof(ch[sz]));
                val[sz]=0;//中间的节点是没有附加信息的 
                ch[u][c]=sz++;//新建节点 
            }
            u=ch[u][c];//往下遍历 
        }
        val[u]=v;//插入附加信息，注意，我们一般只在叶子节点插入附加信息，中间的节点一般是没有附加信息的，因为一个非叶子结点，在Trie中一般都会被不同的单词使用到（定义） 
    }
}tree;

2.查找

接下来是查找操作，事实上查找操作基本上是和插入操作是差不多的，如果你真的理解了上面的insert操作，你可以尝试着在不看我下面代码的情况下去自己写一下，同样，对于这个操作的解释放在代码中

    ll search(char *s){//这里的指针意义同上 
    //对于这一个查找操作，我们就以最简单的操作来展开：
    //查找这个字符串是否在Trie中出现过，如果出现过，返回它的附加信息 
        ll u=0,len=strlen(s+1);
        for(ll i=1;i<=len;i++){
            ll c=idx(s[i]);
            if(!ch[u][c])return -1;
            //没有这个节点，返回-1，即代表这个字符串没有在Trie中出现过
            //这个返回值得看题目所需要的附加信息来决定，因为这里是不可以与附加信息冲突的，在这里我们假定附加信息为0或正数 
            u=ch[u][c];//继续向下遍历 
        }
        return val[u];//这个节点存在，返回它的附加信息 
    }

三.Trie的应用

事实上Trie的应用及其广泛，所以本内容略

显然，上面的代码添麻烦了

精简版trie数组

int son[N][26], cnt[N], idx;
// 0号点既是根节点，又是空节点
// son[][]存储树中每个节点的子节点
// cnt[]存储以每个节点结尾的单词数量

// 插入一个字符串
void insert(char *str) {
    int p = 0;
    for (int i = 0; str[i]; i ++ ) {
        int u = str[i] - 'a';
        if (!son[p][u]) son[p][u] = ++ idx;
        p = son[p][u];
    }
    cnt[p] ++ ;
}

// 查询字符串出现的次数
int query(char *str) {
    int p = 0;
    for (int i = 0; str[i]; i ++ ) {
        int u = str[i] - 'a';
        if (!son[p][u]) return 0;
        p = son[p][u];
    }
    return cnt[p];
}

代码

#include<bits/stdc++.h>
using namespace std;
const int N = 1e6+7;
int trie[N][26],ed[N];
int ct=1,n,m;
char s[N];
void insert() {
    int cur=1;
    for(int i=0;s[i];++i) {
        int ch=s[i]-'a';
        //cout<<cur<<' '<<ed[cur]<<'\n';
        if(!trie[cur][ch]) trie[cur][ch]=++ct;
        cur=trie[cur][ch]; 
    }
    ++ed[cur];
}
int find() {
    int res=0;
    int cur=1;
    for(int i=0;s[i];++i) {
        //cout<<cur<<' '<<ed[cur]<<' '<<res<<'\n';
        int ch=s[i]-'a';
        if(!trie[cur][ch]) {
          cur=trie[cur][ch];
          return res+ed[cur];
        }
        cur=trie[cur][ch];
        res+=ed[cur];
    }
    return res;
}
int main() {
    cin>>n>>m;
    for(int i=1;i<=n;++i) {
        scanf("%s",s);
        insert();
    }
    for(int i=1;i<=m;++i) {
        scanf("%s",s);
        cout<<find()<<'\n';
    } 
    return 0;
}