数据结构 - 二叉堆

二叉堆的定义

二叉堆是一种特殊的堆，二叉堆是完全二元树（二叉树）或者是近似完全二元树（二叉树）。二叉堆有两种：大根堆和小根堆。父结点的键值总是大于或等于任何一个子节点的键值叫做大根堆；父结点的键值总是小于或等于任何一个子节点的键值叫做小根堆。

一图详解二叉堆

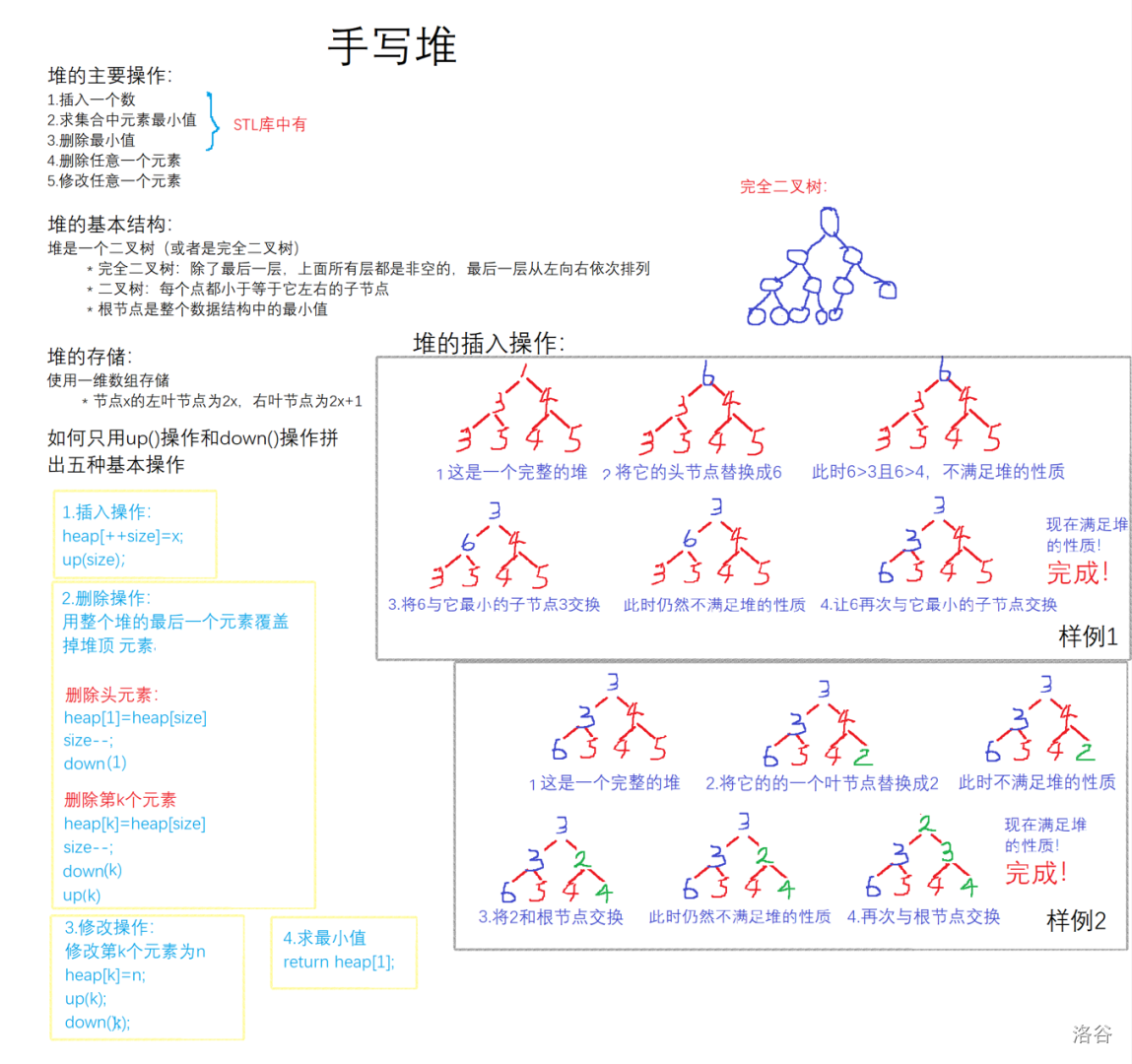
二叉堆的主要操作

插入节点

在数组的最末尾插入新节点。然后自下而上调整子节点与父节点：比较当前节点与父节点，不满足堆性质则交换。从而使得当前子树满足二叉堆的性质。时间复杂度为 $O(\log n)$。

删除根节点

删除根节点用于堆排序。

对于大根堆，删除根节点就是删除最大值；对于小根堆，就是删除最小值。然后，把堆存储的最后那个节点移到填在根节点处。再从上而下调整父节点与它的子节点，直至当前节点与它的子节点满足堆性质为止。

代码实现（小根堆）

//二叉堆
#include<iostream>
#include<algorithm>
using namespace std;
const int N = 1e6+7;
int a[N],last=1; 
void up(int i) {
    if(i==1) return;
    if(a[i]<a[i>>1]) swap(a[i],a[i>>1]),up(i>>1);
    return;
}
void down(int i) {
    if(((i<<1)==last-1)&&(a[i]>a[i<<1]))
        swap(a[i],a[i<<1]),down(i<<1);
    if(((i<<1)<last-1)&&(a[i]>a[i<<1]||a[i]>a[(i<<1)+1])) {
        if(a[i<<1]<a[(i<<1)+1]) swap(a[i],a[i<<1]),down(i<<1);
        else swap(a[i],a[(i<<1)+1]),down((i<<1)+1); 
    }
    return;
}
void insert(int x) {
    a[last]=x;
    last++;
    up(last-1);
}
void putmin() {
    printf("%d\n",a[1]);
}
void popmin() {
    a[1]=a[last-1];
    down(1);
    last--;
}
int main() {
    int k;
    scanf("%d",&k);
    while(k--) {
        int n,t;
        scanf("%d",&t);
        if(t==1) {
            scanf("%d",&n);
            insert(n);
        }
        else if(t==2) putmin();
        else popmin();
    }
    return 0;
}