三分查找

单峰函数

单峰函数是指对于一个函数，在它的值域内，只有一个最大值或一个最小值，在极致两侧，函数保证单调，比如二次函数在实数范围内就是一个标准的单峰函数。

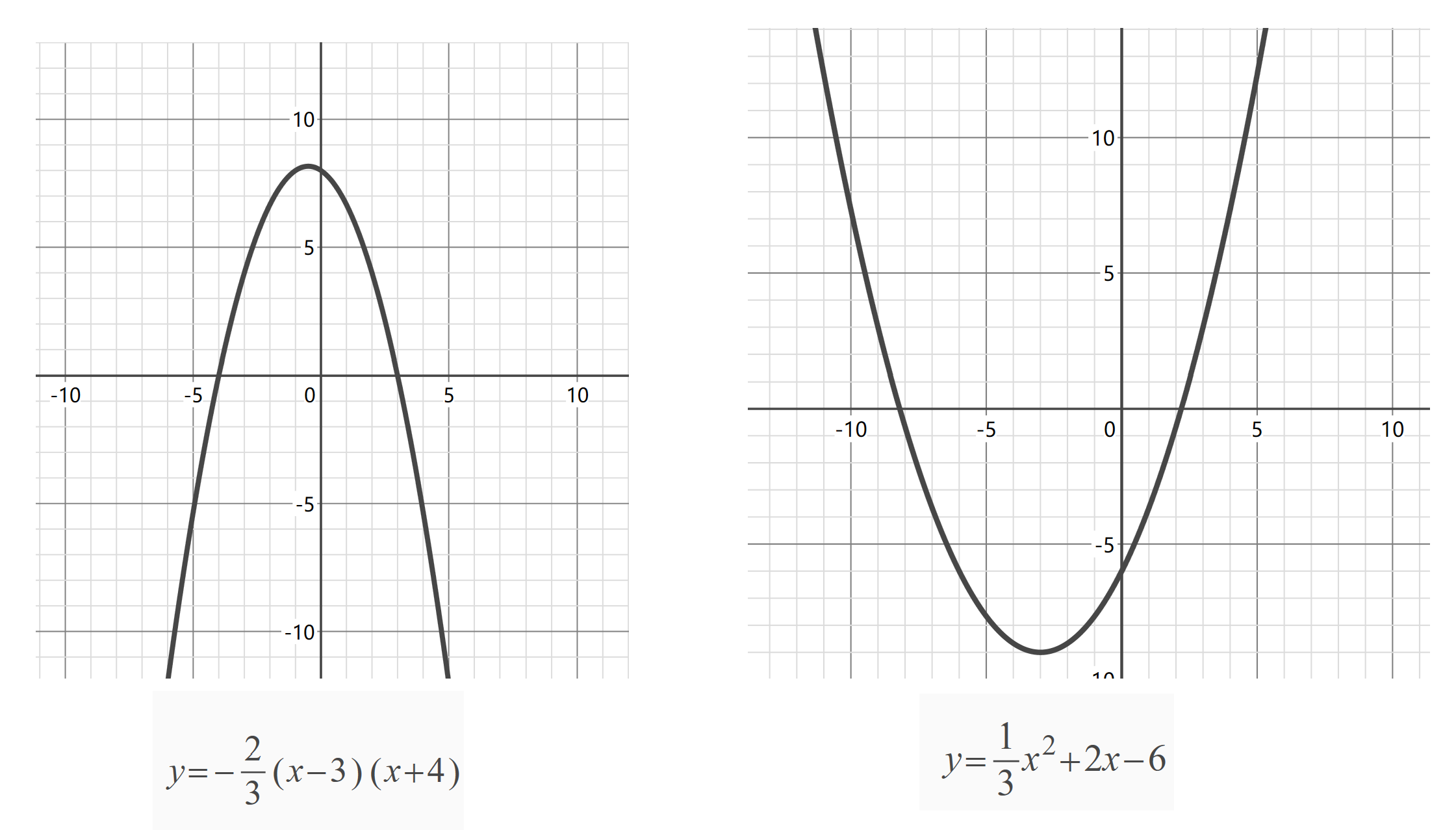
但是要注意的是，单峰函数不一定有一条对称轴，比如高中常见的对勾函数在 \((0,+∞)\) 内就是一个单峰函数，但是它没有一条明确的对称轴。

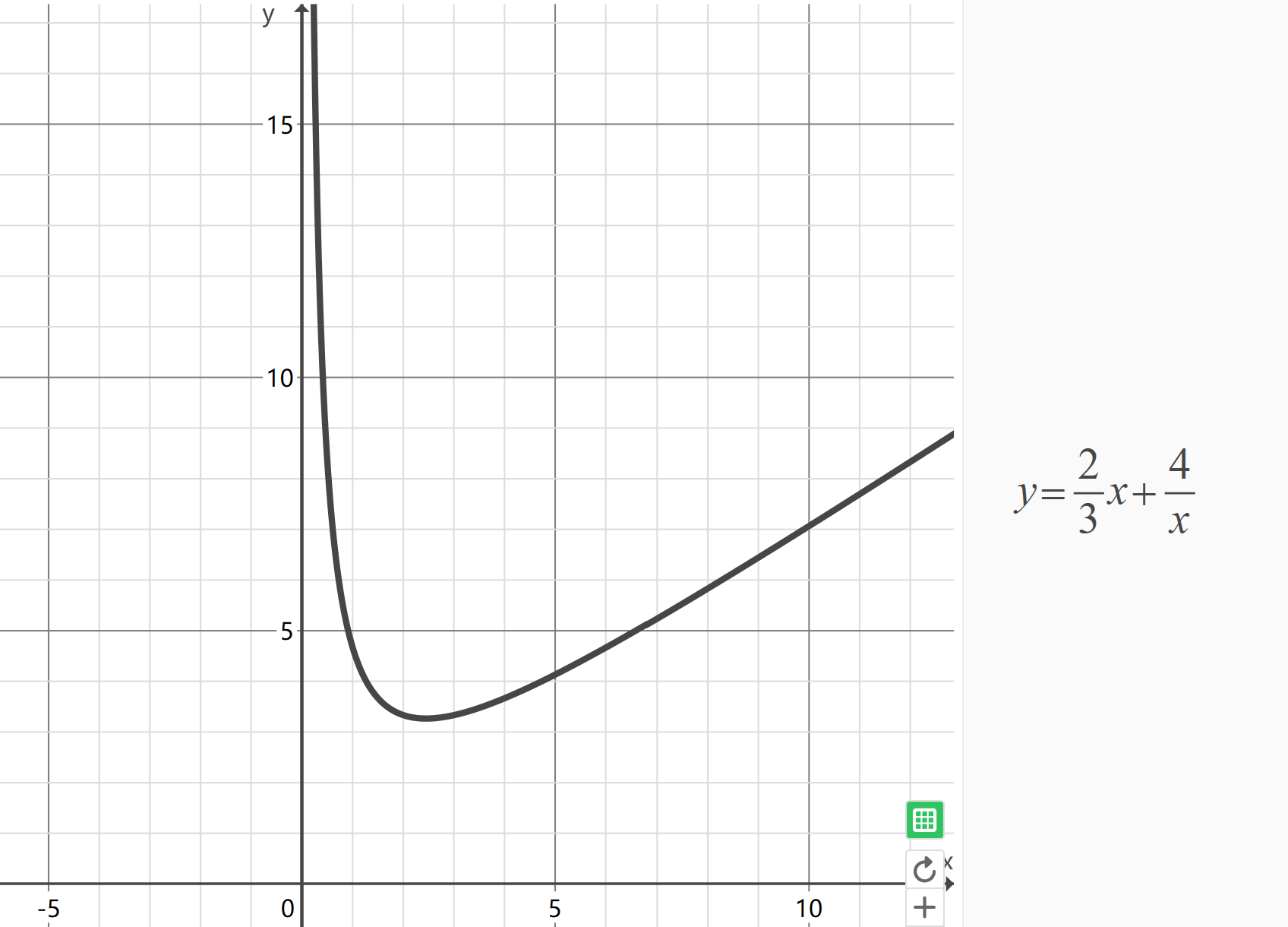
三分查找

What is 三分?

三分是一种查找单峰函数最大或最小值的算法，它的思想和二分差不多，都是通过不断缩小范围来获得最终的答案的，先来简单介绍一下三分的实现过程：

已知某函数顶点的范围（或值域）为 \([l,r]\)，顶点坐标为 \((m,n)\)，求函数最大值，三分过程如下：

• 先在已经确定的值域内找到两个数 \(a\) 和 \(b\)（已知 \(a,b\in [l,r]\)，假设 \(a<b\)）。
• 比较 \(f(a)\) 和 \(f(b)\) 的大小，夹逼区间。

如何夹逼区间是一个重要的问题，试考虑以下四种情况：

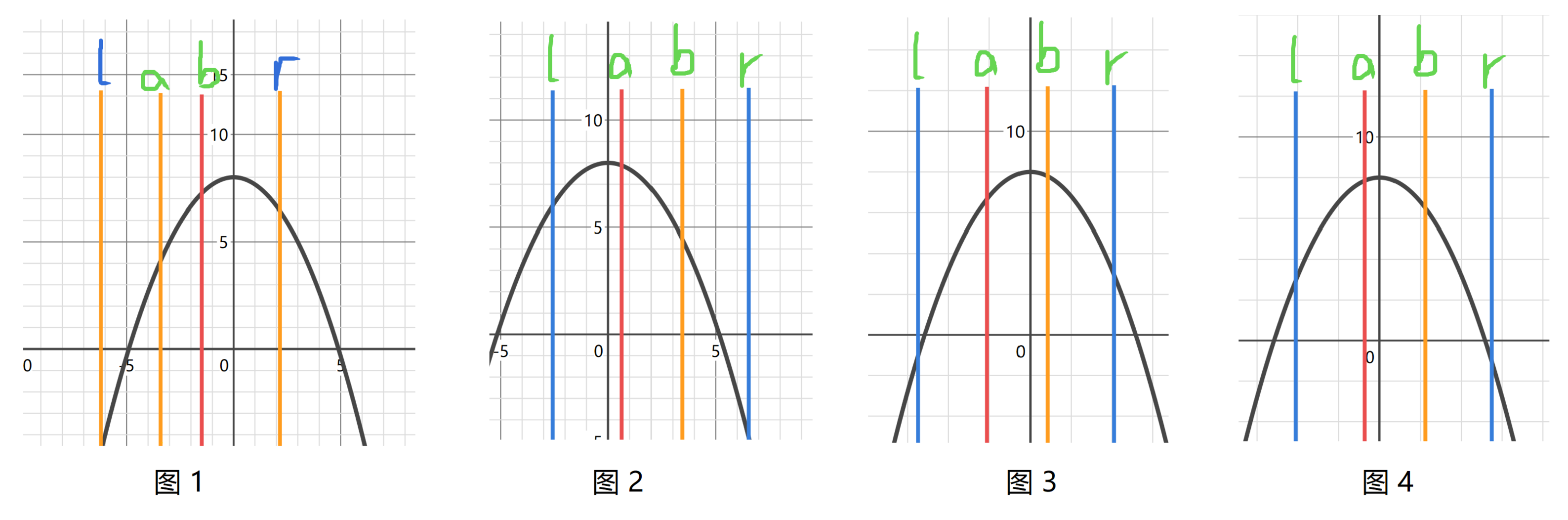
如果 \(f(a)<f(b)\)，如图一或图三所示，那么，加入我们过于激进，直接让 \(l=b\)，对于图三情况，就会发现，\(m\notin [l,r]\)，无法得到答案，如果我们挪动 \(r\)，那么就会发现，无论是让 \(r=a\) 还是 \(r=b\)，对于图一情况，也都会出现 \(m\notin[l,r]\)，所以，唯一的能够保证夹逼区间正确的方式就是让 \(l=a\)。

另一种情况是 \(f(b)\leq f(a)\)，通过对于图二或者图四的尝试，可以知道我们应让 \(r=b\)。

注意：\(a\) 和 \(b\) 的选取方式有很多种。在这里推荐两种比较简单的选取方式：

一是让 \(a=\frac{l+r}{2}\)，\(b=\frac{a+r}{2}\)；

也可以是：\(a=\frac{r-l} 3+a\)，\(b=b-\frac{r-l} 3\)；

后者效率更高但细节更多。

浮点数三分

我们通过一个二次函数来模拟一下浮点数三分的实现过程：

现有二次函数 \(f(x)={x^2}-2x-3\)，因式分解，可转化为 \(f(x)=(x-3)(x+1)\)，由焦点式很容易看出，该二次函数的最小值在 \(x=1\) 时取到，为 \(-4\)，那么，计算机并不知道二次函数的顶点坐标公式，也不知道如何因式分解，对于它来说，求解其顶点坐标的方式简单来说，就是猜。

假设已知该二次函数定点在 \([-10,10]\) 之内，那么我们开始三分，过程如下：

\(id\)	\(l\)	\(r\)	\(a\)	\(f(a)\)	\(b\)	\(f(b)\)
\(\#01\)	\(-10.00\)	\(10.00\)	\(0.00\)	\(-3.00\)	\(5.00\)	\(12.00\)
\(\#02\)	\(-10.00\)	\(5.00\)	\(-2.50\)	\(8.25\)	\(1.25\)	\(-3.94\)
\(\#03\)	\(-2.50\)	\(5.00\)	\(1.25\)	\(-3.94\)	\(3.12\)	\(0.52\)
\(\#04\)	\(-2.50\)	\(3.12\)	\(0.31\)	\(-3.53\)	\(1.72\)	\(-3.48\)
\(\#05\)	\(-2.50\)	\(1.72\)	\(-0.39\)	\(-2.07\)	\(0.66\)	\(-3.89\)
\(\#06\)	\(-0.39\)	\(1.72\)	\(0.66\)	\(-3.89\)	\(1.19\)	\(-3.96\)
\(\#07\)	\(0.66\)	\(1.72\)	\(1.19\)	\(-3.96\)	\(1.46\)	\(-3.79\)
\(\#08\)	\(0.66\)	\(1.46\)	\(1.06\)	\(-4.00\)	\(1.26\)	\(-3.93\)
\(\#09\)	\(0.66\)	\(1.26\)	\(0.96\)	\(-4.00\)	\(1.11\)	\(-3.99\)
\(\#10\)	\(0.66\)	\(1.11\)	\(0.89\)	\(-3.99\)	\(1.00\)	\(-4.00\)
\(\#11\)	\(0.89\)	\(1.11\)	\(1.00\)	\(-4.00\)	\(1.05\)	\(-4.00\)
\(\#12\)	\(0.89\)	\(1.05\)	\(0.97\)	\(-4.00\)	\(1.01\)	\(-4.00\)
\(\#13\)	\(0.97\)	\(1.05\)	\(1.01\)	\(-4.00\)	\(1.03\)	\(-4.00\)
\(\#14\)	\(0.97\)	\(1.03\)	\(1.00\)	\(-4.00\)	\(1.02\)	\(-4.00\)
\(\#15\)	\(0.97\)	\(1.02\)	\(0.99\)	\(-4.00\)	\(1.01\)	\(-4.00\)

上述表格生成代码：

#include <bits/stdc++.h>
#define eps 0.01
using namespace std;
double f(double x) {
	return (x-3.)*(x+1.);
}
signed main() {
	double l=-10,r=10;
	int id=0;
	while(r-l>eps) {
		double a=(l+r)/2.;
		double b=(a+r)/2.;
		printf("#%02d l:%.2f r:%.2f a:%.2f f(a):%.2f0 b:%.2f f(b):%.2f\n",++id,l,r,a,f(a),b,f(b));
		if(f(a)>f(b)) l=a;
		else r=b;
	}
	return 0;
}

浮点数三分练习题：

• 洛谷 P3382
• 洛谷 P1883

整数三分

整数三分的实现过程类似于浮点数三分，是在知道取值范围的情况下，找到能使得答案（函数值）最大/最小的整数值，实现的框架与浮点数三分差别不大，只是有些关键点需要注意，我们以函数 \(y=(x-2.5)(x+1)\) 为例，加入我们知道它的最小值范围在 \([-20,20]\) 之间，那么，程序最终会找到一个范围，\([l,r]\) 表示函数的最小值可能出现的范围 \([l,r]\)，如下表：

\(id\)	\(l\)	\(r\)	\(a\)	\(f(a)\)	\(b\)	\(f(b)\)
\(\#01\)	\(-20\)	\(20\)	\(0\)	\(-2.50\)	\(10\)	\(82.50\)
\(\#02\)	\(-20\)	\(10\)	\(-5\)	\(30.00\)	\(2\)	\(-1.50\)
\(\#03\)	\(-5\)	\(10\)	\(2\)	\(-1.50\)	\(6\)	\(24.50\)
\(\#04\)	\(-5\)	\(6\)	\(0\)	\(-2.50\)	\(3\)	\(2.00\)
\(\#05\)	\(-5\)	\(3\)	\(-1\)	\(-0.00\)	\(1\)	\(-3.00\)
\(\#06\)	\(-1\)	\(3\)	\(1\)	\(-3.00\)	\(2\)	\(-1.50\)
\(\#07\)	\(-1\)	\(2\)	\(0\)	\(-2.50\)	\(1\)	\(-3.00\)
\(\#08\)	\(0\)	\(2\)	\(1\)	\(-3.00\)	\(1\)	\(-3.00\)

final range: \([0,1]\)

生成代码：

// author: syl
// language: c++
#include <bits/stdc++.h>
#define eps 0.01
using namespace std;
double f(double x) {
	return (x-2.5)*(x+1.);
}
signed main() {
	int l=-20,r=20;
	int id=0;
	while(r-l>1) {
		int a=(l+r)/2;
		int b=(a+r)/2;
		printf("#%02d l:%d r:%d a:%d f(a):%.2f0 b:%d f(b):%.2f\n",++id,l,r,a,f(a),b,f(b));
		if(f(a)>f(b)) l=a;
		else r=b;
	} printf("final range: [%d,%d]\n",l,r);
	return 0;
}

在得到了一个最终的答案范围 \([l,l+1]\) 时，就很容易得到最小值了，具体做法就是判断一下 \(f(l)\) 和 \(f(l+1)\) 的大小，然后返回就可以了，所以完整代码如下：

还有一种写法是 \(a=\lfloor\frac{r-l+1} 3\rfloor+a\)，\(b=b-\lfloor\frac{r-l+1} 3\rfloor\)。

#include <bits/stdc++.h>
#define eps 0.01
using namespace std;
double f(double x) {
	return (x-2.5)*(x+1.);
}
signed main() {
	int l=-20,r=20;
	int id=0;
	while(r-l>1) {
		int a=(l+r)/2;
		int b=(a+r)/2;
		printf("#%02d l:%d r:%d a:%d f(a):%.2f0 b:%d f(b):%.2f\n",++id,l,r,a,f(a),b,f(b));
		if(f(a)>f(b)) l=a;
		else r=b;
	} printf("final range: [%d,%d]\n",l,r);
	printf("%d %.2lf\n",(f(l)>f(r)?r:l),min(f(l),f(r)));
	return 0;
}