SciTech-Mathmatics-Probability+Statistics: The Scientific Method科学研究方法 & Engineering Design工程 + Population VS Sampling(Hypothesis of Parameters) + Likelyhood VS Probability(Model of Solid Parameters)
SciTech-Mathmatics-Probability+Statistics: Differences:
The Scientific Method & Engineering Design


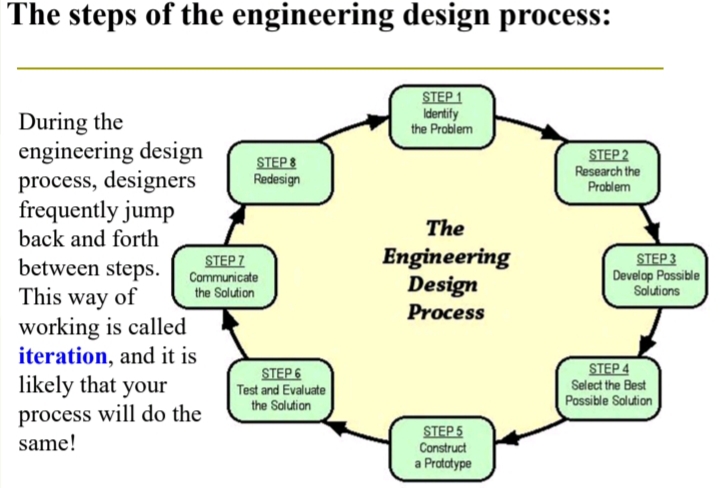
Population Vs Sample



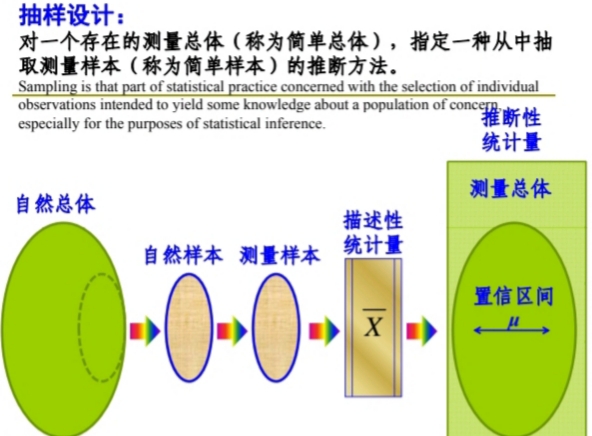
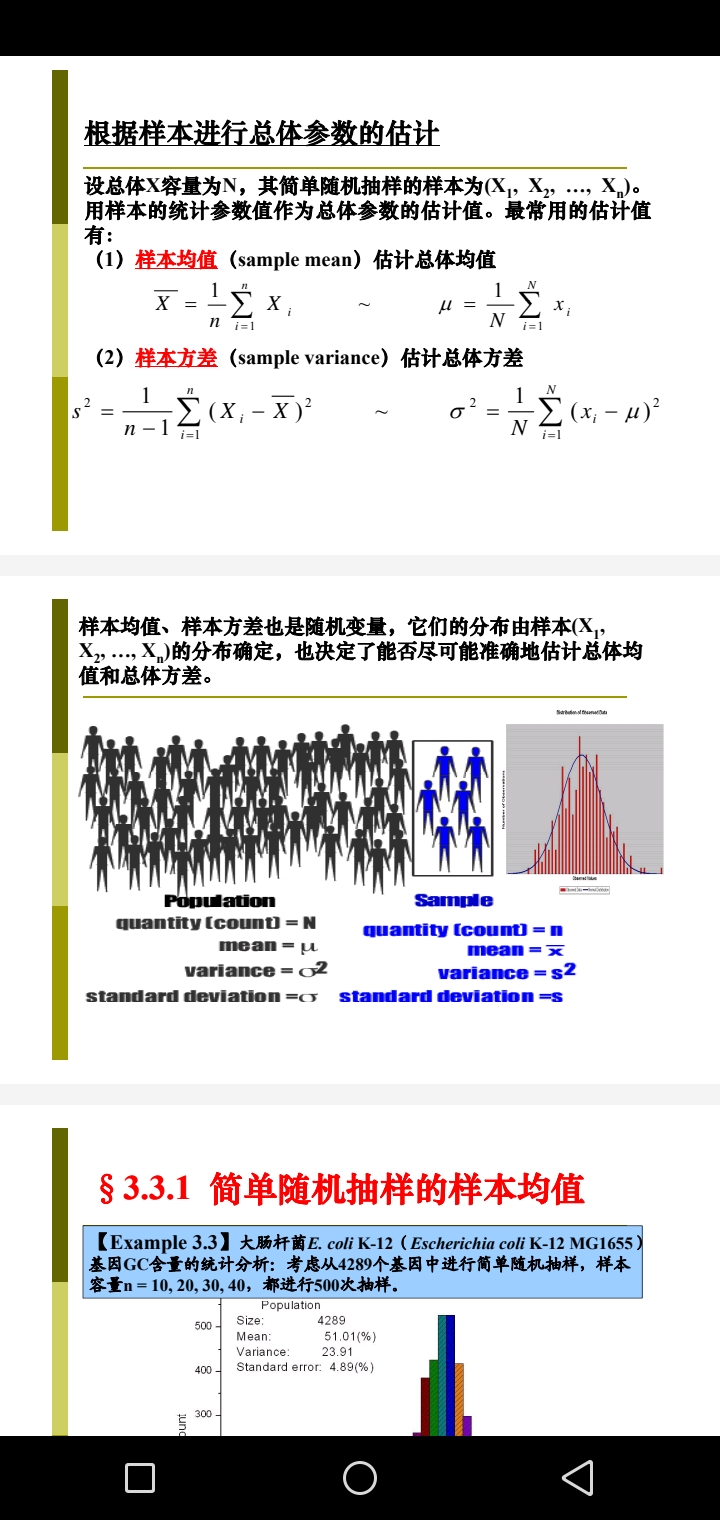
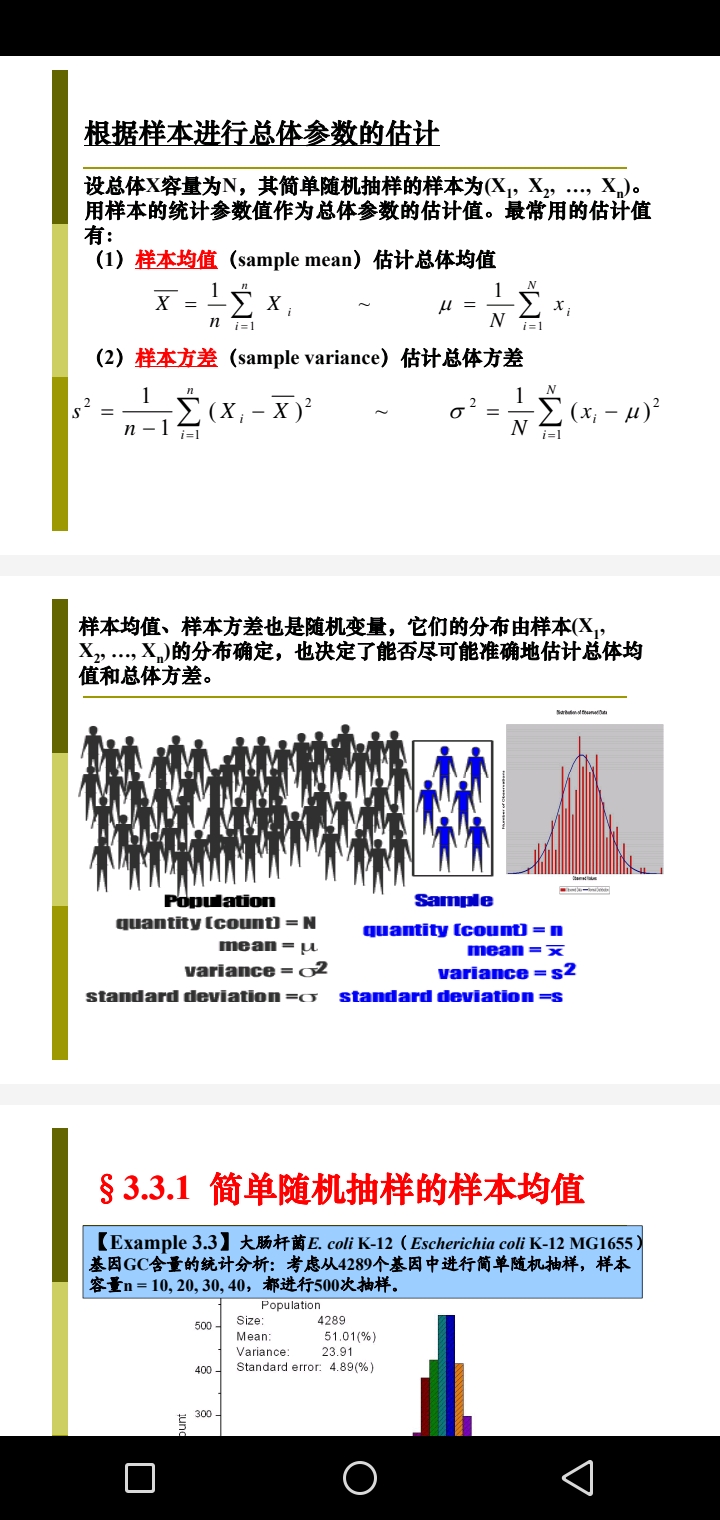
Statistics and Statistical Observation
![]()
11.
![]()
12.
![]()
13.
![]()
14.
![]()
15.

Likelyhood VS Probability
Process·Outcome ·Experiment · Hypothesis · Testing · Parameters ·Probability ·Distribution
Likelyhood => one Parameter of a Model
Probability => one Outcome of a Process
- “抛硬币模型”,第一步,只能确定“Only two kinds of outcome”:
只能“判断”这类“Experiment”应当 ~ b(n, p)“Bernoulli Distribution”。
但是“硬币”被证实是“fair coin”之前,参数p(probability of head) 是“待检验(校准)”的。 - Likelyhood 的 testing hypothesis 阶段:
找到“一堆硬币”,要一个个的“检验”得到其为“fair coin”的 Likelyhood (通过大量试验).
并通过试验可以确定每一个硬币的p(head); - Probability游戏阶段:
"Subjective Judgement and Decision-Making" 选用那一枚 "coin" 进行 "Game";
"选用方":- 已经确定 "抛硬币" 的 "process" 只有两种 "outcome" 时, 作为 "experiment".
- 选用“检验过”的硬币\(\large C_x\) 后,"Game" 的 Probability 及 Distribution 为 \(\large b(n, p_x)\) 就可用来预测。
Likelyhood 阶段
如何检验(校准):只能通过“Scientific Method”检验.
对于“硬币”的“检验(校准)”:
- 在experiment 之前,根据“经验或判断”给出的是 Prior Probability.
- 只能先拿到“sample data”of “experiments”;
预先抛100次或更多,通过观察“number of head ”;
计算“真实试验概率”假如 100次 只有 17次,则 p(heads) = 0.17
这个 0.17 是 Posterior( 真实的 “sample data”和真实 “experiments”得到的), - 根据实际“experiment”和 “sample data”判断“fair coin”的假设。
如果 Hypothesis 的 Posterior 与 Prior 两概率的Variance(偏差) 过大;则换硬币。
如果 Hypothesis 的 Posterior 与 Prior 两概率的Variance(偏差)在允许范围,则检验通过。 - 在一堆硬币经过“检验”后,每一枚硬币的 Parameter 都可以得到;
例如 3 枚硬币,C1的p 为0.4, C2的p 为0.5, C3的p 为0.6;
至于何时选用 C1, C2, C3 进行下一阶段的“Probability Game”由人自主决定。
Probability 阶段
“fair coin”已经检验完成,即 “process”到“experiment”, 再到确定好 b(n,p)的 Parameter p;
假设“检验过”3 枚硬币,C1的p 为0.4, C2的p 为0.5, C3的p 为0.6;
- 选用 C3, head 出现的概率要大,而且 p(head) = 0.6
- 选用 C1, head 出现的概率要小,而且 p (head) = 0.4
- 选用 C2, head 与 tail 概率等同,即 p (head) = 0.5, 这是一枚真实的 fair coin.
即 Empirical Probability是通过“人为布局设计”可“操控”的;
而 Theoritical Probability是理论“Equally likely outcomes”
对 Subjective Probability是主观根据“belief”和“information of process”给出“judgement”.
Likelyhood VS Probability
Likelihood vs. Probability: What's the Difference?
BY ZACH BOBBITTPOSTED ON AUGUST 18, 2021
Two terms that students often confuse in statistics are likelihood and probability.
Here's the difference in a nutshell:
Probability refers to the chance that a particular outcome occurs based on the values of parameters in a model.
Likelihood refers to how well a sample provides support for particular values of a parameter in a model.
- When calculating the probability of some outcome, we assume the parameters in a model** are trustworthy, and the sample data can well represent corresponding population.
- However, when we calculate likelihood we're trying to determine if we can trust the parameters in a model based on the sample data that we've observed, furthermore if we can trust the sample data.
The following examples illustrate the difference between probability and likelihood in various scenarios.
Example 1: Likelihood vs. Probability in Coin Tosses
Suppose we have a coin that is assumed to be fair. If we flip the coin one time, the probability that it will land on heads is 0.5.
Now suppose we flip the coin 100 times and it only lands on heads 17 times. We would say that the likelihood that the coin is fair is quite low. If the coin was actually fair, we would expect it to land on heads much more often.
When calculating the probability of a coin landing on heads, we simply assume that P(heads) = 0.5 on a given toss.
However, when calculating the likelihood we're trying to determine if the model parameter (p = 0.5) is actually correctly specified.
In the example above, a coin landing on heads only 17 out of 100 times makes us highly suspicious that the truly probability of the coin landing on heads on a given toss is actually p = 0.5.
Example 2: Likelihood vs. Probability in Spinners
Suppose we have a spinner split into thirds with three colors on it: red, green, and blue. Suppose we assume that it’s equally likely for the spinner to land on any of the three colors.
If we spin it one time, the probability that it lands on red is 1/3.
Now suppose we spin it 100 times and it lands on red 2 times, green 90 times, and blue 8 times. We would say that the likelihood that the spinner is actually equally likely to land on each color is very low.
When calculating the probability of the spinner landing on red, we simply assume that P(red) = 1/3 on a given spin.
However, when calculating the likelihood we're trying to determine if the model parameters (P(red) = 1/3, P(green) = 1/3, P(blue) = 1/3) are actually correctly specified.
In the example above, the results of the 100 spins make us highly suspicious that each color is equally likely to occur.














 浙公网安备 33010602011771号
浙公网安备 33010602011771号