SciTech-Mathmatics-Physics-Particle Physics-Election+Photon+Quantum: Parallel Universe + Superposition + Wave-Particle Duality.

SciTech-Mathmatics-Quantum
LaTex: https://tex.stackexchange.com/questions/483996/automatically-sized-bra-ket-in-quantum-physics

Complex
Euler
Gauss
Hilbert Space

\(Superposition\ States\) VS \(Binary\ Logic\)

the \(\large Fundamental\ Difference\) between \(Binary\ Logic\) and \(Superposition\ States\).
two ideas of the micro world.

Schrodinger's Cat

• Traditional Interpretation: Either live(1) or die(-1),

• Superposition Interpretation of Quantum Mechanics: Superposition of the two quantum states.
  $\large f = 50\% \cdot quantum(Left) + 50\% \cdot quantum(Right) $
  this equation seems a little bit like the Expectation Equation of Probability Theory.
  hypotheses, \(\large quantum(Left) = +1 ; quantum(Rightl)=-1\)
  then $\large f = 50\% \cdot (+1) + 50\% \cdot (-1) = 0 $

• (Schrödinger equation, Schrodinger wave equation)

Dirac's Bra & Ket

Superposition Equation of Quantum States

• \(\large Linear\ Combination\ Form(Bra \& Ket) Expression\) of Superposition of Quantum Mechanics:
  Using Advanced Linear Algebra to analysis the Quantum Mechanics.
  \(\large \begin{array}{lll} \\ Hypotheses, \text{ There are totally } n\ kinds \text{ of } observed\ outcomes. \\ \text{ the Superposition state }before\ observation \text{ is }: \end{array}\)
  \(\large \begin{array}{rll} \\ SuperPosition_c &=& c_1 \cdot quantum(1) + c_2 \cdot quantum(2) + \cdots + c_n \cdot quantum(n) \\ \end{array}\)

• Dirac's normalized Vector Form of Quantum Mechanics:

  • each state of superposition can be expressed as a vector \(\large ket\), written as \(\large \ket \phi\)
    then the Superposition state can also be written as:
    \(\large \begin{array}{rll} \\ SuperPosition_c &=& c_1 \cdot \ket {E_1}+ c_2 \cdot \ket {E_2{E_1}} + \cdots + c_n \cdot \ket {E_n} \\ \end{array}\)

  • Inner products of two vectors "bra" $\large \bra \Psi $ and "ket" $\large \ket \Phi $
    \(\large \begin{array}{rll} \\ \bra{\Psi} \ket{\Phi} \\ \bra \psi \ket \phi \\ \end{array}\)

  • 泛函空间，矢量vector就是 函数。
    那么，假设我们的函数全都是幂函数（或可用Taylor Equation逼近)，形式如下。
    则：\(\large \begin{array}{rll} \\ f &=& c_0 \cdot x^0 + c_1 \cdot x^1 + \cdots + c_n \cdot x^n + \cdots \\ e^x &=& \frac{1}{1} \cdot x^0 + \frac{1}{1!} \cdot x^1 + \frac{1}{2!} \cdot x^2 + \cdots + \frac{1}{n!} \cdot x^n + \cdots\\ \end{array}\)

Probability : Expectation

Wave-Particle Duality: Double-slit Experiment
https://brilliant.org/wiki/double-slit-experiment/

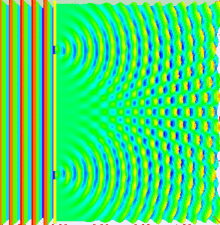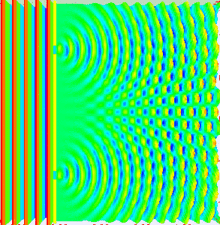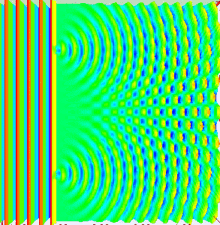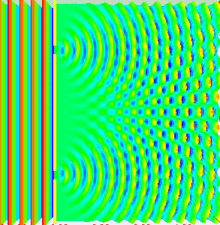
The Maxwell Equations:

• Election, Substances, Particle's Brown Movements
• AZD(Absolute Zero Degree): Each kind of particle has its wave when above AZD.
• The Maxwell Equations:
  \(\large \begin{array}{llll} \\ (\ i\ ) & \bm{\nabla} \cdot \bm{D} &= 4 \pi \rho_{f} \ , & \text{静电荷产生电场}；\\ (ii\ ) & \bm{\nabla}\cdot \bm{B} &= 0 \ , \text{静磁场磁通量总和为0, 不存在单磁极} \\ (iii) & \bm{\nabla} \times \bm{E} &= -\frac{\partial\bm{B}}{\partial t}\ , \text{变化的电场感生变化磁场，有函数关系} \\ (iv\ ) & \bm{\nabla} \times \bm{H} &= \bm{J}_f + \frac{\partial\bm{D}}{\partial t}\ , \text{变化的磁场感生变化电场，有函数关系} \\ \end{array}\)

Hilbert Space

TED Speech:
HARTMUT NEVEN - Leader of Quantum Computing Lab of Google
APRIL2024, VANCOUVER BC.

Parallel Universe： 平行宇宙
Superposition: 叠加态

Traditional Computation:

• Binary Logic of 0s and 1s
• Applications: today's computers like: your laptop and servers of Google Data-Center.

Quantum Computer:

• replaced these binary logics with the Law of Quantum Physics