SciTech-BigDataAIML-LLM-Transformer Series-$\large Supervised\ Statistical\ Model$监督学习的统计模型+$\large Transformer+Self Attention$的核心原理及实现

SciTech-BigDataAIML-LLM-Transformer Series>

$\large Supervised\ Statistical\ Model$:

$\large Transformer+Self Attention$

$\large Supervised\ Model$: Supervised by $\large Training\ Data$.
$\large Statistical\ Model$: mainly using Probability+Statistics methods.
both $\large Transformer$ and $\large Self Attention$ are $ Supervised\ Statistical\ Model $
分“训练(学习)阶段”和“预测(应用)阶段”:
- 训练阶段: 在 "大量训练数据" 上 "学习总结事实规律"(确定模型参数),
  主流用统计概率分析方法.
  例如: $\large Self Attention$ 训练时确定最好的模型参数$\large W^q,\ W^k, W^v$.
- 预测阶段: 可重复使用的应用"预先总结的(训练数据的)事实规律"进行快捷高效的预测.
  例如: $\large Self Attention$ 预测时，直接用训练好的 $\large W^q,\ W^k, W^v$ 高效预测 .
$\large Transformer$ 及 $\large Self Attention$ 都是 $\large Supervised\ Statistical\ Model$
是对"大量预训练数据", 用"统计概率分析等方法", 学习总结"事实规律"(确定模型参数),
以能可重复使用的应用"预先总结的事实规律"进行快捷高效的预测的模型.
$\large Self Attention$预测时的"乱序计算出稳定" $\large Attention\ Score\ Vector$ "能力
- $\large Self Attention$预测用 $\large Parameter$ 是"稳定不变"预先训练好存在模型的.
  即: 计算Word Sequence任意两个"Word"的$\large Attention\ Score$时, 用的 $\large W^q,\ W^k, W^v$ 是稳定不变的训练好的模型参数.
- 任意乱序计算稳定的" $\large Attention\ Score\ Vector$ " 能力:
  "Word Sequence"任意重排, 得到同一 $\large Attention\ Score\ Vector$(如果不嵌入 $\large PE位置信息$).
$\large Transformer$的核心原理:
是组合使用多种"数学驱动"的先进技术:
- $\large Self Attention$,
- $\large PE(Positional\ Encoding)$,
- $\large WE(Word\ Embedding)$.
实现以下多种优点:
- 解耦"Long Sequence"(长序列)的"强顺序依赖(Word的前后位置)",
- 可并行计算 $\large Attention\ Score\ Vector$,
- 可伸缩性$\large Scalability$.

$\large Mathmatical\ Definition$

$\ of\ the\ Self Attention$

Given $\text{ a sequence of input tokens }$:

\[X_1,\ X_2, \cdots ,\ X_n,\ where\ X_i \in R^d,\ 1 \leq d \leq n, d is the dimension number of each input token \]

, its $Self-Attention$ outputs $\text {a sequence of the same length} $: $ Y_1,\ Y_2, \cdots ,\ Y_n$, where:
\ Y_i \in R^d,\ 1 \leq d \leq n, d is the dimension number of each input token $$

, where

(11.6.1)
according to the definition of attention pooling in (11.1.1). Using multi-head attention, the following code snippet computes the self-attention of a tensor with shape (batch size, number of time steps or sequence length in tokens,
). The output tensor has the same shape.

$\large Self-Attention$ 的优点与缺点

$\large Self-Attention$ 的缺点:
- 小模型时, 开销较大。
- Word之间没有"顺序关系":
  打乱一句Word Seq.后, $\large Self-Attention$仍是计算每两个Word的$\large Attention\ Score$。
  Transformer 是用上PE(Positional Encoding), 使得每一Word(Embedding)"都嵌入有位置顺序信息"(在 $\large Self-Attention$ 并行计算 $\large Attention\ Score$ 时)。
  而且能并行计算 $\large Attention\ Score$, 不必串行(一定计算完前一Word才能计算当前Word).
$\large Self-Attention$ 的优点:
- 解决了"长序列依赖", 支持 "变长"的特长序列。
- 可$\large Parallel$ (并行)计算 $\large Attention\ Score$, 易 $\large Scaleability$。
  大模型时，特别的合适。
- $\large Self-Attention$的$\large W^q,\ W^k, W^v$ 都是统计分析"预训练数据"总结的规律.
  也就是, 用"不同统计分布"的"预训练数据", 就可"训练出"对应行为的统计监督模型。
  统计模型一旦设计好, 就可以"只更新 预训练数据", 而不必修改 模型.
- $\large Input$可以是$\large 模型Input$, 也可是$\large Hidden\ Layers$(隐藏层,非Input或Output).
- $\large Seq2Seq$模式: $\large Output$是 "模型决定可变长度的" 的 $\large Output\ Sequence$.

1. Vectorize(向量化) and Matrixize(矩阵化) 不同的$\large Input$ 数据

常用的数据类型有Text/Picture/Audio/Video/Graph:如社交网与分子图

Attention(注意力) 与 Self-Attention(自注意力)

1. 传统"$\large Stepping\ Slip\ Window$"采样方法

$\large Input$ 为"变长"Matrix(Vector Sequence)时,
"$\large Stepping\ Slip\ Window$"(步进式滑动窗口)采样,
采集 $\large COM(Co-Occurrence\ Matrix)$ 及$\large Context$的方式,
只能增大$\large Length\ of\ Slip\ Window$ 以适应"变长"$\large Input$.
不易实现"$\large Scaleability$可伸缩性.

Google的 $\large Transformer$ 及 $\large Self-Attention$ 易实现 $\large Scaleability$.

$\large Self-Attention$自注意力机制

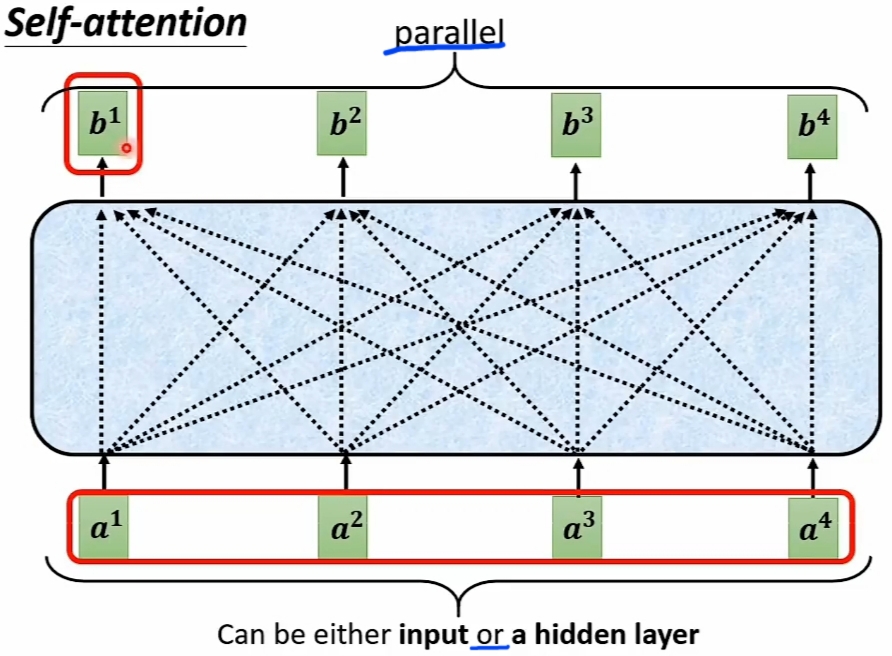
$\large Self-Attention$ 可与 $\large FC$(全连接层) 多层交替堆叠使用

$\large Self-Attention$的目标:

计算变长 $\large Vector\ Seq.$ 的任何两个 $\large Vector$ 的 $\large Attention(Relevant)\ Score$:

$\large Self-Attention$自注意力的实现

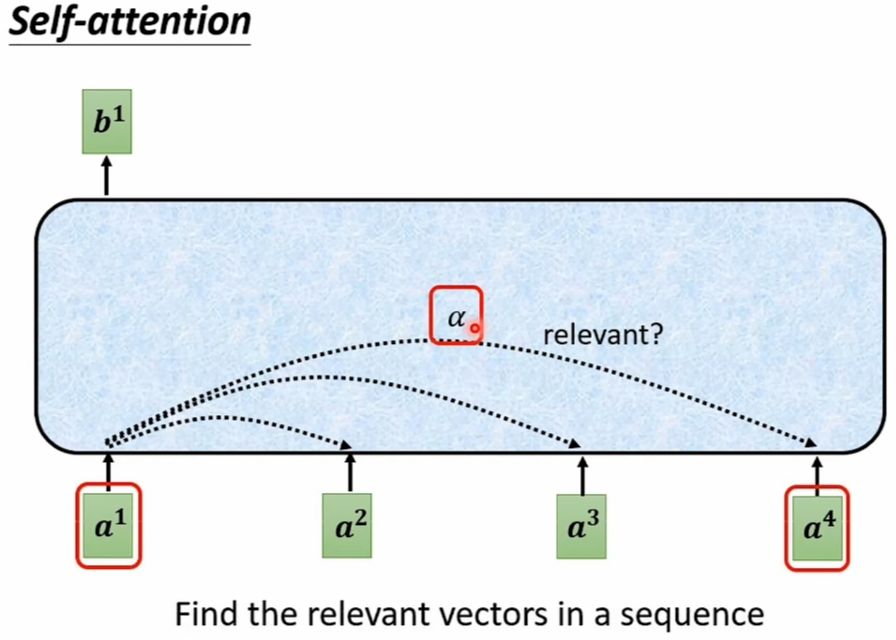
中心任务是 "Find the relevant vectors in a sequence":
$\large Self-Attention$的$\large Dot-Product$ 与 $\large Additive$ 实现，常用前一种。
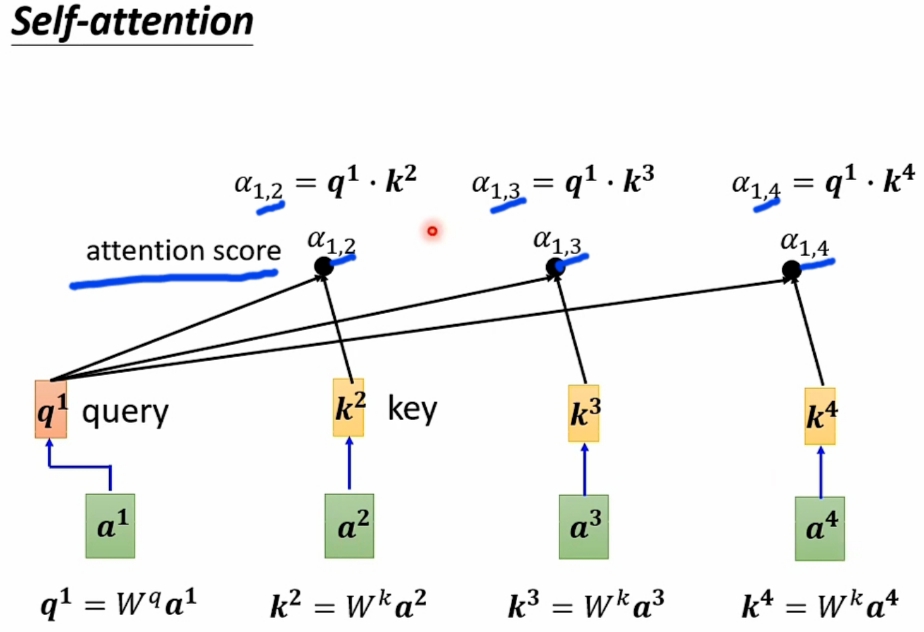
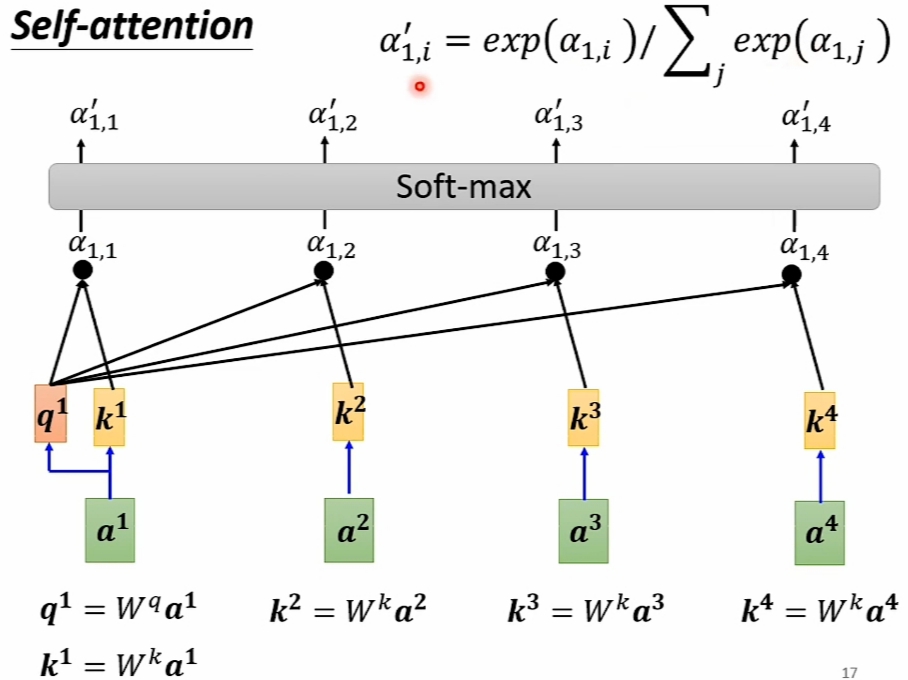
$\large Self-Attention$ 的 $\large Dot-Product$ 实现精解
$\large Hypothesis$ :
- $\large Input\ Vector\ Sequence$ 是$\large [a^1, a^2, a^3, a^4]$
- 求解的 $\large Output\ Vector\ Sequence$ 设为:
  $\large [\alpha_{1,1}, \alpha_{1,2}, \alpha_{1,3}, \alpha_{1,4}, \ \alpha_{2,1},\alpha_{2,2},\alpha_{2,3},\alpha_{2,4}, \ \alpha_{3,1}, \alpha_{3,2},\alpha_{3,3},\alpha_{3,4}, \ \alpha_{4,1}, \alpha_{4,2},\alpha_{4,3},\alpha_{4,4}]$
- 以求解$\large [\alpha_{1,1}, \alpha_{1,2}, \alpha_{1,3}, \alpha_{1,4}]$为例: