编程-单调栈

 

单调栈 单调递减栈，栈底到栈顶，元素依次减小。

个人认为是比武栈。

有个土财主要嫁闺女，全城的小伙子都想去试试，4.1号正式开始招亲，3.31大家就来排队。本来是是按照先来后到的顺序进行排队，但是排在后面的武功高的人不服气，就把前面武功不如自己的打跑了。

一直遇到排在自己前面武功比自己高强的人，他才会老老实实的排队。

最后演变成：每来一个人，都会和队尾的人比较，能打得过，就把他打跑，一直遇到自己打不过的人，再老老实实的排队，被打跑的人，会掏个小本本，默默的记下打跑自己的人，君子报仇，十年不晚。

这样，每一个被打跑的人，都知道在自己后面，离自己最近的，比自己厉害的人是谁；每一个能留在队中的人，都可以和地主说，我后面没有比我更加厉害的了，你把女儿嫁给我吧。

代码如下：

  

class Solution {
public:
    vector<int> nextGreaterBoys(vector<int>& boys) {
        stack<int> st;
        vector<int> res(boys.size(), -1);

        for (int i = 0; i < boys.size(); ++i) {
            while (!st.empty() && nums[i] > nums[st.top()]) {
                res[st.top()] = nums[i];
                st.pop();
            }
            st.push(i);
        }
        return res;
    }
};

 

42. 接雨水

给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

示例 1：

输入：height = [0,1,0,2,1,0,1,3,2,1,2,1]
输出：6
解释：上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图，在这种情况下，可以接 6 个单位的雨水（蓝色部分表示雨水）。 

示例 2：

输入：height = [4,2,0,3,2,5]
输出：9

class Solution {
public:
    int trap(vector<int>& heights) {

        int result = 0;
        stack<int> st;

        //寻找最近的比自己大于等于的值
        for (int i = 0; i < heights.size(); ++i) {
            while (!st.empty() && heights[i] >= heights[st.top()]) {
                int j = st.top();
                st.pop();
                if (!st.empty()) {
                    result += ((min(heights[st.top()], heights[i]) - heights[j]) * (i - st.top() - 1));
                }

            }
            st.push(i);
        }
        return result;
    }
};

int main()
{
    Solution s;
    vector<int> v{0,1,0,2,1,0,1,3,2,1,2,1};
    //vector<int> v{4,3,2};
    cout << s.trap(v);
}

 https://blog.csdn.net/weixin_42784951/article/details/88963758

84. 柱状图中最大的矩形

给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。

求在该柱状图中，能够勾勒出来的矩形的最大面积。

 

 

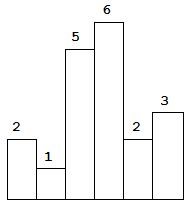
 以上是柱状图的示例，其中每个柱子的宽度为 1，给定的高度为 [2,1,5,6,2,3]。

 

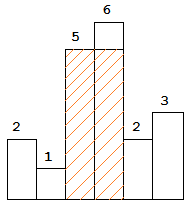
 图中阴影部分为所能勾勒出的最大矩形面积，其面积为 10 个单位。

 示例:

输入: [2,1,5,6,2,3]
输出: 10

 

class Solution {
public:
    int largestRectangleArea(vector<int>& heights) {

        int result = 0;
        stack<int> st;
        vector<int> res(heights.size(),heights.size());

        //正序寻找最近的比自己小的值
        for (int i = 0; i < heights.size(); ++i) {
            while (!st.empty() && heights[i] < heights[st.top()]) {
                res[st.top()] = i;
                st.pop();
            }
            st.push(i);
        }

        stack<int> st2;
        vector<int> res2(heights.size(),-1);

        //逆序寻找最近的比自己小的值
        for (int i = heights.size() - 1; i >= 0; --i) {
            while (!st2.empty() && heights[i] < heights[st2.top()]) {
                res2[st2.top()] = i;
                st2.pop();
            }
            st2.push(i);
        }


        for (int i = 0; i < heights.size(); ++i) {
            int tmp = (abs(res2[i] - res[i]) - 1) * heights[i];
            result = max(result, tmp);
            //cout << tmp << " ";
        }
        return result;
    }
};

 

 

496. 下一个更大元素 I

给你两个 没有重复元素 的数组 nums1 和 nums2 ，其中nums1 是 nums2 的子集。

请你找出 nums1 中每个元素在 nums2 中的下一个比其大的值。

nums1 中数字 x 的下一个更大元素是指 x 在 nums2 中对应位置的右边的第一个比 x 大的元素。如果不存在，对应位置输出 -1 。

示例 1:

输入: nums1 = [4,1,2], nums2 = [1,3,4,2].
输出: [-1,3,-1]
解释:
    对于 num1 中的数字 4 ，你无法在第二个数组中找到下一个更大的数字，因此输出 -1 。
    对于 num1 中的数字 1 ，第二个数组中数字1右边的下一个较大数字是 3 。
    对于 num1 中的数字 2 ，第二个数组中没有下一个更大的数字，因此输出 -1 。

示例 2:

输入: nums1 = [2,4], nums2 = [1,2,3,4].
输出: [3,-1]
解释:
    对于 num1 中的数字 2 ，第二个数组中的下一个较大数字是 3 。
    对于 num1 中的数字 4 ，第二个数组中没有下一个更大的数字，因此输出 -1 。

提示：

• 1 <= nums1.length <= nums2.length <= 1000
• 0 <= nums1[i], nums2[i] <= 104
• nums1和nums2中所有整数 互不相同
• nums1 中的所有整数同样出现在 nums2 中

 

 

class Solution {
public:
    vector<int> nextGreaterElement(vector<int>& nums1, vector<int>& nums2) {
        stack<int> st;
        vector<int> result(nums1.size(), -1);
        if (nums1.size() == 0) return result;

        unordered_map<int, int> umap; // key:下表元素，value：下表
        for (int i = 0; i < nums1.size(); i++) {
            umap[nums1[i]] = i;
        }
        st.push(0);
        for (int i = 1; i < nums2.size(); i++) {
            while (!st.empty() && nums2[i] > nums2[st.top()]) {
                if (umap.count(nums2[st.top()]) > 0) { // 看map里是否存在这个元素
                    int index = umap[nums2[st.top()]]; // 根据map找到nums2[st.top()] 在 nums1中的下表
                    result[index] = nums2[i];
                }
                st.pop();
            }
            st.push(i);
        }
        return result;
    }
};

 

 

 

503. 下一个更大元素 II

给定一个循环数组（最后一个元素的下一个元素是数组的第一个元素），输出每个元素的下一个更大元素。数字 x 的下一个更大的元素是按数组遍历顺序，这个数字之后的第一个比它更大的数，这意味着你应该循环地搜索它的下一个更大的数。如果不存在，则输出 -1。

示例 1:

输入: [1,2,1]
输出: [2,-1,2]
解释: 第一个 1 的下一个更大的数是 2；
数字 2 找不到下一个更大的数； 
第二个 1 的下一个最大的数需要循环搜索，结果也是 2。

class Solution {
public:
    vector<int> nextGreaterElements(vector<int>& nums) {
        int size = nums.size();
        stack<int> st;
        vector<int> res(size,-1);

        for (int i = 0; i < 2 * size - 1; ++i) {
            while (!st.empty() && nums[i % size] > nums[st.top() % size]) {
                res[st.top()] = nums[i % size];
                st.pop();
            }
            st.push(i % size);
        }
        return res;
    }
};