日期问题大部分不会有很高的思维难度,因为对日期时间的概念是我们从现实生活中得到“模拟”的,只是可能会在枚举日期的基础上复杂化一些条件。
直接举实例:
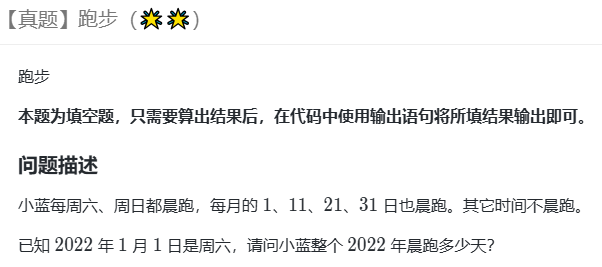
问题并不复杂,代码也简单易懂:
using namespace std;
int main()
{
int month[]={31,28,31,30,31,30,31,31,30,31,30,31};
int week=6,run_day=0;
for(int month_d:month){
for(int day=1;day<=month_d;day++){
if(week==6||week==0||day==1||day==11||day==21||day==31){
run_day+=1;
}
week=(week+1)%7;
}
}
cout<<run_day;
return 0;
}
因为此题年份2022我们直接就知道它不是闰年,若涉及年份跨度,还需要添加:
//0用于占位,由此每个索引位置数字即为该索引月份的天数
int days_in_month[] = {0, 31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31};
// 判断闰年
bool is_leap_year(int year) {
return (year % 4 == 0 && year % 100 != 0) || (year % 400 == 0);
}
// 获取某月的天数
int get_days_in_month(int year, int month) {
if (month == 2 && is_leap_year(year)) {
return 29;
}
return days_in_month[month];
}
再对其中枚举提取星期时,令星期等于星期加一模除7即可,但是注意每个数字到底对应的是星期几。
稍复杂的题目由大家自己练手了,下面我介绍一种蔡勒(Zeller)算法,可以快速获取具体一天是星期几,其公式为:
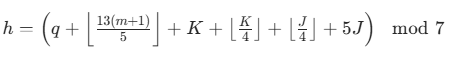
其中h及星期几(0 = 星期六,1 = 星期日,2 = 星期一,…,6 = 星期五);q代表日(1-31);m代表月(3=3 月,4=4 月,…,14 = 次年 2 月);K代表年的后两位(如 2024 年 K=24);J代表年的前两位(如 2024 年 J=20)
其中需要注意1月和2月视为上一年的13月和14月(如2024年1月视为2023年13月),它计算出的h在实际算法运用需要调整为常用的星期表示。
运用实例:
#include <iostream>
#include <string>
#include <cmath> // 用于floor函数
using namespace std;
// Zeller公式计算星期几
// 返回值:0=星期日,1=星期一,...,6=星期六
int zeller(int year, int month, int day) {
// 处理1月和2月(视为上一年的13、14月)
if (month < 3) {
year--;
month += 12;
}
int q = day; // 日
int m = month; // 月(3-14)
int K = year % 100; // 年的后两位
int J = year / 100; // 年的前两位
// 应用Zeller公式
int h = q + static_cast<int>(13 * (m + 1) / 50) + K + K / 4 + J / 4 + 5 * J;
h %= 7;
// 调整结果:将0=星期六转换为6,1=星期日转换为0等
// 最终:0=星期日,1=星期一,...,6=星期六
return (h + 6) % 7;
}
int main() {
int year, month, day;
cout << "请输入日期(格式:年 月 日):";
cin >> year >> month >> day;
// 简单的日期有效性检查
if (month < 1 || month > 12 || day < 1 || day > 31) {
cout << "输入的日期无效!" << endl;
return 1;
}
// 计算星期几
int weekday = zeller(year, month, day);
// 星期名称数组
string weekdayNames[] = {"星期日", "星期一", "星期二", "星期三", "星期四", "星期五", "星期六"};
// 输出结果
cout << year << "年" << month << "月" << day << "日是" << weekdayNames[weekday] << endl;
return 0;
}
虽说它能用到的概率十分小,就当开拓视野了吧,此类算法也很丰富,如“世界末日”算法、奇克森算法等等......



