模拟算法就是按照题目中的一些规则,一步步模拟其操作过程,许多题目还需联系现实的解决方法。它适用于规则明确、无需特殊动态算法的问题。虽然相对较简单,但它是解决复杂现实问题的基础。
我们直接看实际问题:
假设有一个m×n个地块的矩形房间,每个地块初始有按行为主序的连续整数,现在从(0,0)位置放置一个清扫机器人,它只能延顺时针以螺旋状地清洁整个房间,现输入该房间规模m,n,要求给出它具体的行进路线,完成整个房间的清扫。如一个4×3的房间,行进路线如图:
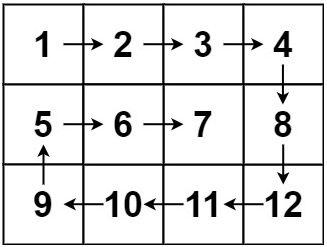
最终输出路线[1,2,3,4,8,12,11,10,9,5,6,7]。(改编自leetcode-54)
——模拟清扫机器人的实际路线,先向右直行到头,再转向下、转向左、转向上,循环直至遍历完整个房间。由此,我最先想到的是使用up,down,left,right来收缩房间的边界,实现这样“螺旋状”的遍历。初始化up与left为房间的上方、左方待清扫区域,均为0,right为房间地块的列数、down为房间地块的行数。随后在上下边界、左右边界不相撞的情况下,按序遍历将地块号加入新列表即可。
点击查看代码
class Solution(object):
def spiralOrder(self, room):
right=len(room[0])
down=len(room)
r=[]
up=left=0
while(up < down and left < right):
for i in range(left,right):
r.append(room[up][i])
up+=1
for i in range(up,down):
r.append(room[i][right-1])
right-=1
if up<down:
for i in range(right-1,left-1,-1):
r.append(room[down-1][i])
down-=1
if left<right:
for i in range(down-1,up-1,-1):
r.append(room[i][left])
left+=1
return r
该算法的时间复杂度为O(N²),且需要维护四个边界变量,容易出错,其实仔细想想,压缩待清扫区域,不如直接压缩“房间”,毕竟题目没有对房间地块的其它操作了,直接模拟“削层”即可——每次取出房间一个边界上的一整排地块数据,直至房间“没了”。
点击查看代码
class Solution(object):
def spiralOrder(self, room):
r=[]
while room:
r.extend(room.pop(0))
if room and room[0]:
for k in room:
r.append(k.pop())
if room:
r.extend(room.pop()[::-1])
if room and room[0]:
for k in room[::-1]:
r.append(k.pop(0))
return r
可以看到少了四个边界变量后,虽然时间复杂度没有变换,但是代码一下简洁了很多..对吧。
看下一个题目:(取自蓝桥云课-3766)

对于此题我初步想法是直接模拟其前进方式,存储所有能抵达的石头编号,只要输入中需要求解的最大石头编号大于当前能抵达的最大石头编号,就一直递推。最后获取每个询问的石头编号在可抵达组could中的索引即为消耗步数。代码如下:
点击查看代码
n=int(input())
ask=[]
could=[1]
for _ in range(n):
a=int(input())
ask.append(a)
i=0
while max(could)<max(ask):
m=could[i]+sum(int(c)for c in str(could[i]))
could.append(m)
i+=1
for i in range(n):
if could.count(ask[i])==0:
print(-1)
else:
print(could.index(ask[i]))
哦不!调试时顺利通过,但运行时只有40%通过率,其它全部超时!
我们回头仔细看看,题目中需要的是询问石头的具体步数,而非“能否到达”——因此我们还需要一个step用以记录石头的步数,仅凭借could.index方法效率过低。剪枝上,我们再添加最大石头编号最大为10的六次方。另外还有一点关键,max(ask)>max(could)的循环条件并不能涵盖所有的情况,大家可以思考一下为什么。
点击查看代码
n=int(input())
ask=[]
could=[1]
for _ in range(n):
a = int(input())
ask.append(a)
step={1:0}
max_=10**6
i=0
while i<len(could)and(not ask or max(could)<max(ask)):
m=could[i]+sum(int(c)for c in str(could[i]))
if m not in step and m<max_:
step[m]=step[could[i]]+1
could.append(m)
i+=1
for target in ask:
if target not in step:
print(-1)
else:
print(step[target])
你以为这就结束了吗,其实这样写依旧超时了。问题的根源其实是sum(int(c)for c in str(could[i]))这一段,当数字较大时效率极低,所以虽然写起来方便,但我们还是老老实实写成函数吧。再次,由于测试时喜欢使用较大的数值,我们应避免使用频繁的列表遍历等操作,直接使用数值进行索引与存储,最终可得:
点击查看代码
n=int(input())
ask=[]
for _ in range(n):
a=int(input())
ask.append(a)
step={1:0}
max_ask=max(ask) if ask else 0
max_=max_ask+200
# 只生成到“目标最大值+200”,无需1e6(够覆盖所有可达目标)
current=1
def get_sum(x):
s=0
while x:
s+= x%10
x//=10
return s
while current<max_:
if current in step:
x= get_sum(current)
m= current+x
if m not in step and m<max_:
step[m]= step[current] + 1
current+=1
for target in ask:
print(step.get(target, -1))


