机器学习第二次作业

学习笔记

第一章 基本概念

模式识别的形式

• 分类
  • 输出是离散的
• 回归
  • 输出是连续的

回归是分类的基础，离散的类别值由回归值做判别决策得到。

特征的特性

• 具有辨别能力：基于统计学规律
• 鲁棒性：抗干扰性，稳健性

特征向量的相关性

• 点积
  • 对称性
• 投影
  • 不具备对称性
• 残差向量
• 欧氏距离
  • 综合考虑方向和模长

机器学习流程图

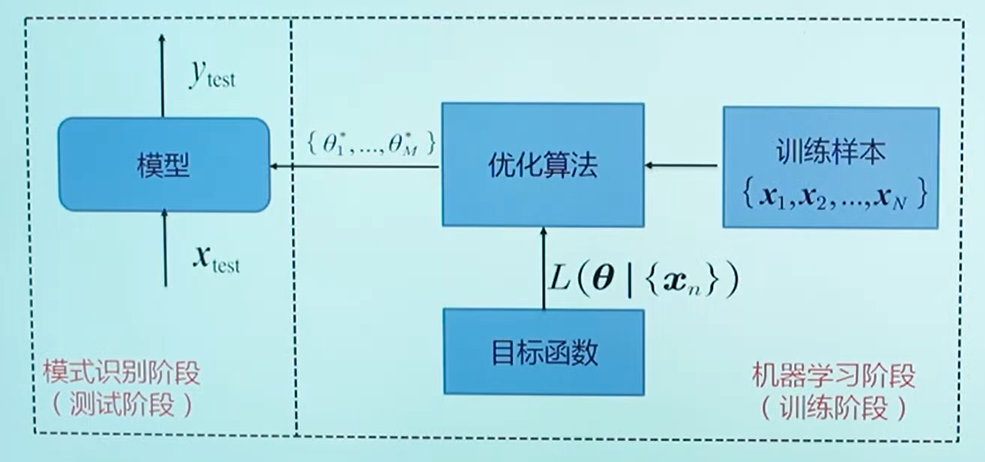
目标函数的作用：参数可能没有准确解或有无数解，所以要确定近似解

机器学习的方式

• 监督式学习：给定训练样本和输出真值
  • 应用：识别、分类
• 无监督式学习：不给定输出真值（更难）
  • 根据训练样本之间的相似程度决策
  • 应用：聚类、图像分割
• 半监督式学习
• 强化学习：机器自行探索决策、真值滞后反馈的过程
  • 应用：棋类

误差

• 训练误差
• 测试误差（泛化误差）

泛化能力

模型不仅对训练样本有决策能力，也对新的模式有决策能力。

• 过拟合：训练阶段很好，测试阶段很差

提高泛化能力：

• 选择复杂度适合的模型
  • 训练样本的个数N，多项式阶数M
• 正则化：在目标函数中加入正则项

模型评估方法

• 留出法
  • 随机划分训练集和测试集
  • 多次划分取平均
• K折交叉验证
  • K个子集，取一个作为测试集
  • 重复K次，每个子集都测试一次，取平均
• 留一验证
  • K=样本总数的K折交叉验证

性能指标

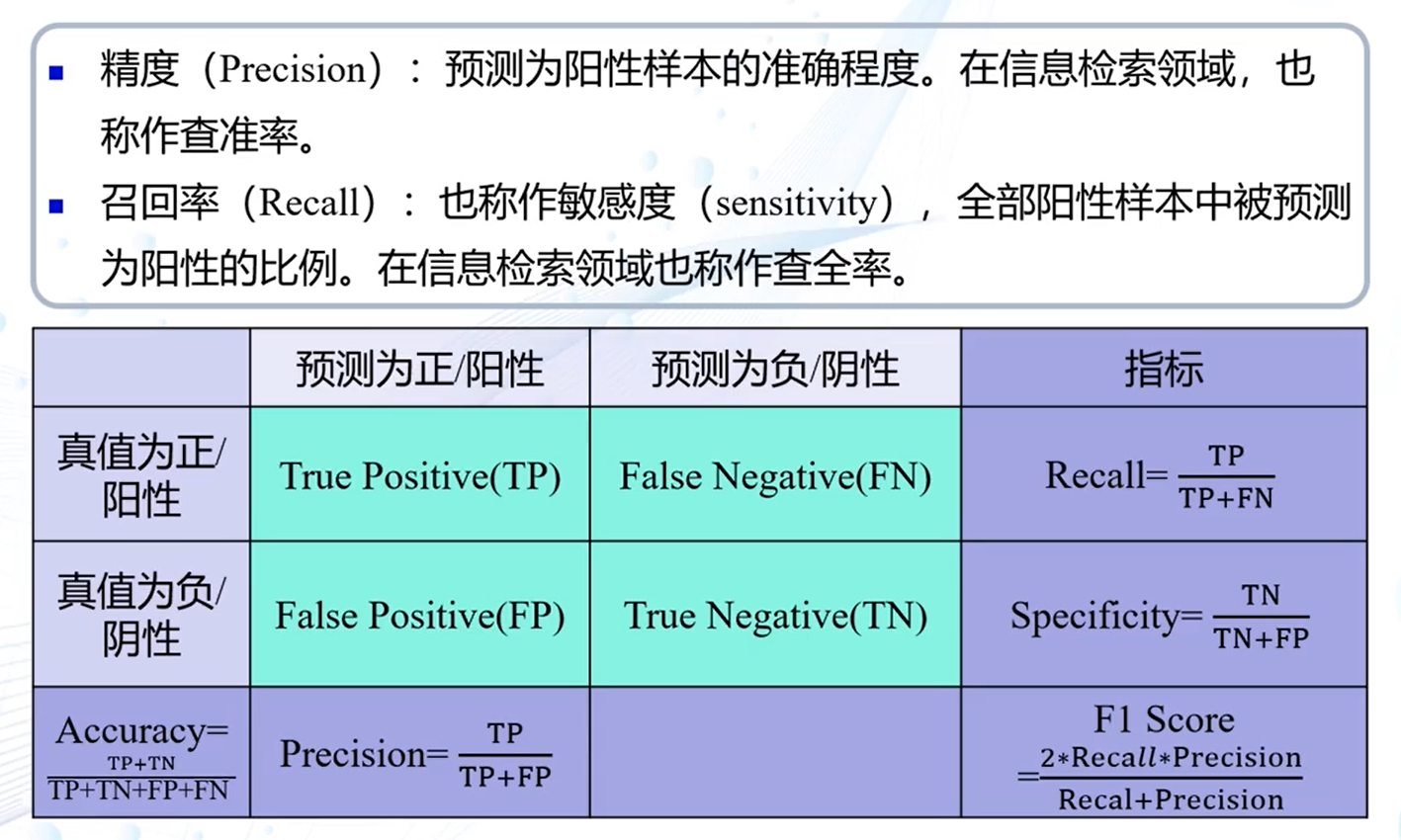
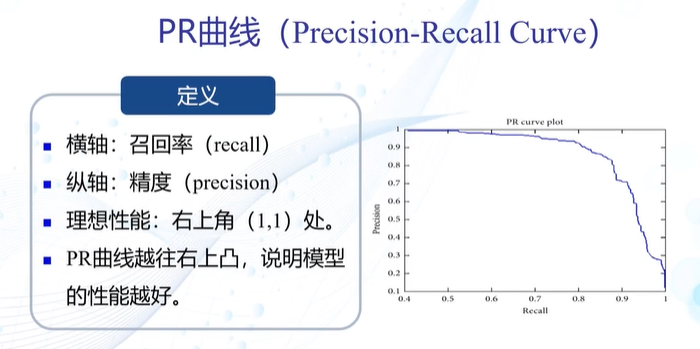
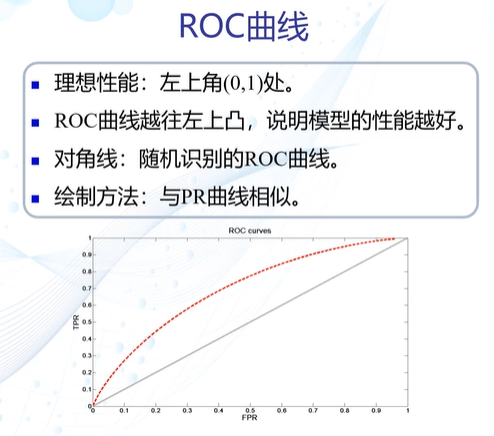
第二章 基于距离的分类器

类的原型

代表这个类的一个模式或一组量

• 均值
  • 误差最小
• 最近邻
  • 取决于测试样本的位置
  • 误差较大
  • 对噪声和异常样本较敏感

距离度量

标准：

• 同一性
• 非负性
• 对称性
• 三角不等式

方式：

• 欧氏距离
• 曼哈顿距离
• 加权欧氏距离

MED分类器

最小欧氏距离分类器

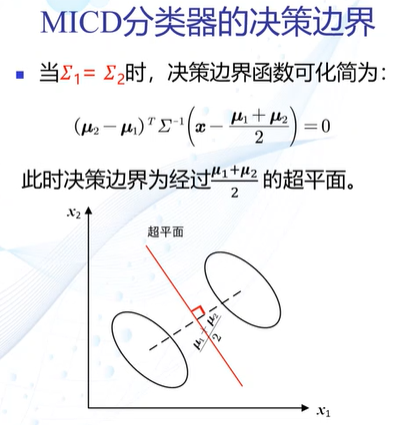
决策边界：超平面，垂直平分两个类原型的连线

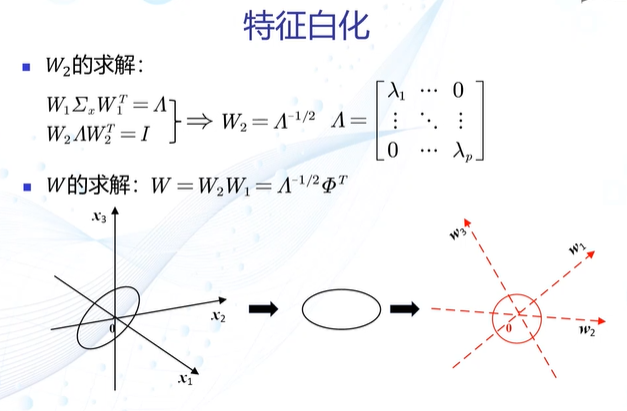
特征正交白化

去除特征方差不同和特征相关性

• 解耦：协方差矩阵对角化，去除相关性
• 白化：尺度变换，使各维方差相同

MICD分类器

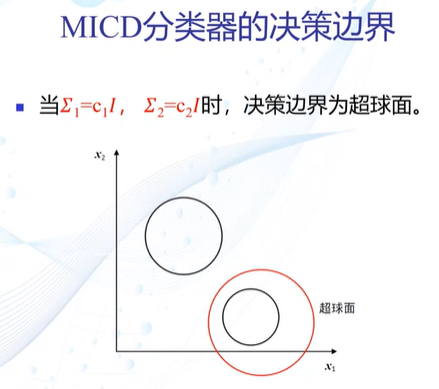
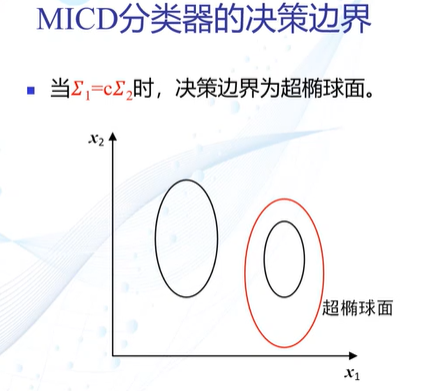
最小类内距离分类器（马氏距离）

决策边界：

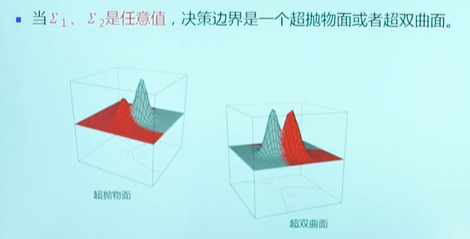
缺陷：

会选择方差较大的类

原因：仅考虑观测到的训练样本的分布情况，没有考虑类的分布等先验知识

第三章 贝叶斯决策与学习

后验概率 p(C|x)

• 输入模式x：随机变量或向量
• 类别输出C：随机变量

给定模式x属于类C的可能性

贝叶斯规则

MAP分类器

最大后验概率分类器

决策边界：

• 单维：两条
• 高维：复杂的非线性边界

决策误差

未选择的类所对应的后验概率

• 单个测试样本：p(error|x)
• 所有测试样本：均值，p(error)

观测概率

• 单维高斯分布
  • 方差相等时：一条，决策边界偏向先验概率小的类，即分类器决策偏向先验概率高的类（注意表述的不同）
  • 方差不等时：两条，非线性，分类器决策倾向于方差小的类
• 高维高斯分布
  • 决策边界是超二次型

损失

当前决策动作相对于其他候选类别的风险程度

假定x属于Cj，决策动作αi的损失：λ(αi|Cj)，简称λij

可以用矩阵表示

决策风险

定义：所有候选类别的期望损失

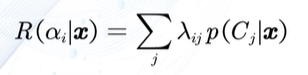
贝叶斯分类器

决策风险最小

• 决策损失

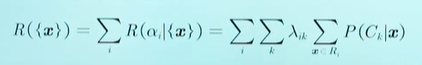
• 决策目标

最小化期望损失：对每个测试样本选择风险最小的类

朴素贝叶斯分类器

特征是多维的，假定特征之间是独立的

拒绝选项

• 原因：决策边界附近的判别有较大不确定性

引入阈值τ，后验概率小于τ的决策会被拒绝

τ∈(1/K,1)

学习心得

课程结束的有点快，这些天的学习中接触了很多关于机器学习和模式识别的新概念，新知识。由于以前从来没接触过相关领域，所以这门课程有点难学，但也正因如此，这些东西对我来说也都很新鲜，让我想要了解更多。

第一节课上，了解了很多模式识别和机器学习领域的应用，意识到机器学习技术与人们日常生活的密切联系，比如无人驾驶，文字识别，人脸识别，股市预测等等各种应用，才发现在智能设备如此普及的现在，人们的生活早已离不开机器学习技术的支撑，明白了机器学习的重要性。之后，在老师深入浅出的讲解下，从机器学习的基本概念和原理，到分类器的讲解以及优化，我了解了越来越多的知识。

同样的，这门课也让我明白了基本功的重要。。由于对之前线代、高数等知识的淡忘，在一些公式推导方面，学习的有些吃力。而课本又都不在家里，没法随时查阅相关知识，所以对公式这方面学习的确实不怎么扎实，以后肯定还要回过头来再看几遍才能掌握。。