最佳牛围栏

最佳牛围栏

给出长度为n数列\(\{a_i\}\)，求其中的一段子段的平均数的最大值，并且保证子段长度大于等于f，\(1≤n≤100000\)。

解

[警告：此题卡精度]

法一：二分

这是一道有关单调性的问题，不太好二分，可考虑写出二分式，不妨记最优解为\(\bar{x}\)，那么对于最优解有

\[\frac{\sum_{i=l}^ra_i}{r-l+1}=\bar{x} \]

经过式子变换有其二分式

\[\sum_{i=l}^r(a_i-\bar{x})=0 \]

于是只要判断左式答案与0的关系，就可以确定是否有最优解了，当左式的最大值大于0时，我们就可以知道\(\bar{x}\)可以更加优秀，反之，于是问题变成如何求左式的最大值，不妨构造新数列\(\{b_i\}\)，有\(b_i=a_i-\bar{x}\)，现在问题转化为求数列\(\{b_i\}\)的最大子段和

我们自然想到原来的贪心模型，从数列左向右确定子段的右端点，当右端点到了某个位置事子段和小于0时，左端点从此处令起。

但是此题有长度限制，注意到原问题也可以看成区间问题，于是枚举右端点r，再枚举左端点l的上一个位置，不妨记\(\{B_i\}\)为\(\{b_i\}\)前缀和，于是所求最大值即\(s_r-s_l\)，注意到在枚举右端点r时，\(s_r\)为定值，只要寻找到\(s_l\)的最小值即可，每次r向右移，就增加一个决策点，只要用一个变量保存最优解，每次和新进来的决策点比较取大小即可,只能做到\({\large O(nlog_2^n)}\)。

参考代码：

#include <iostream>
#include <cstdio>
#define il inline
#define ri register
#define lb double
#define exact 0.00001
#define intmax 0x7fffffff
using namespace std;
lb b[100001];
int a[100001],n,f;
template<class free>
il free Max(free,free);
il bool check(lb);
int main(){
	scanf("%d%d",&n,&f);
	for(int i(1);i<=n;++i)
		scanf("%d",&a[i]);
	lb l(1),r(2000),mid;
	while(l+exact<=r){
		mid=(l+r)/2;
		if(check(mid))l=mid;
		else r=mid;
	}printf("%d",(int)(r*1000));
	return 0;
}
template<class free>
il free Max(free a,free b){
	return a>b?a:b;
}
il bool check(lb x){
	for(int i(1);i<=n;++i)
		b[i]=a[i]-x,b[i]+=b[i-1];
	int l(0);lb ans(-intmax);
	for(int r(f);r<=n;++r){
		ans=Max(ans,b[r]-b[l]);
		if(b[r-f+1]<b[l])l=r-f+1;
	}return ans>=0;
}

法二：斜率优化

设\(f_i\)为前i个数的最优解，显然有

\[f_i=\max_{0\leq j<i}\{\frac{s_i-s_j}{i-j}\} \]

注意到这个类似斜率的东西，先考虑单调性，其中\(j,s_j\)显然是单调递增的，至于\(f_i\)未知，于是问题可以转化成求点\((i,s_i)\)与点集\(\{(j,s_j)\}\)的一个点所连的一条直线的斜率最大值

对于任意三个点A,B,C考虑，设A，B是决策点，C与i有关，即\((i,s_i)\)，按照当初推出凸壳的方法，对于任意三个点考虑，只有下图两种情况，而且注意到一个性质，C的横坐标和纵坐标都在递增，而且总在决策点右方

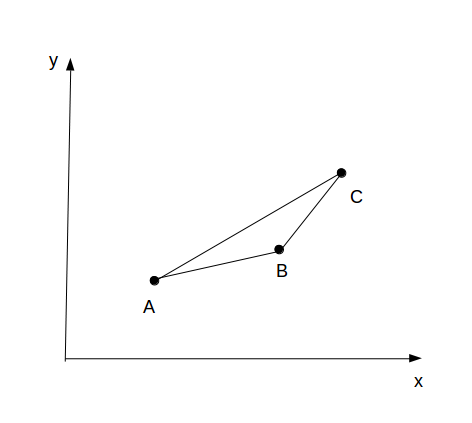
对于该图，容易知道决策点取点B比A更优秀,我们不妨将它叫做下凸三角形（多形象啊），特点是\(k_{AB}<k_{BC}\)，而且随着i的增大，C点无论如何，只有这个上凸三角形继续变成一个下凸三角形，才有可能成为最优解，否则当它变成下凸三角形，其结果不会比原来的优秀。

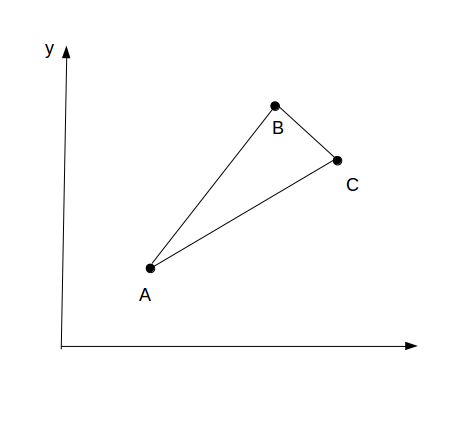
对于该图，容易知道决策点A比B更加优秀，我们不妨将它叫做上凸三角形，特点为\(K_{AB}>K_{AC}\)，而且随着i的增大，这个三角形有可能从上凸三角形变为下凸三角形

（注：根据两幅图的总结，更加本质的性质即c是否在直线AB的上方）

而这只能告诉我们任意三个点中哪个决策点会更加优秀，不能推广到大量的点，于是我们的找一个图形的载体维护，使能够成为最优决策点的答案都在上面，自然想到凸壳，用单调队列维护一个下凸壳，这样在凸壳上方的点，无论如何都不会是最优决策点。

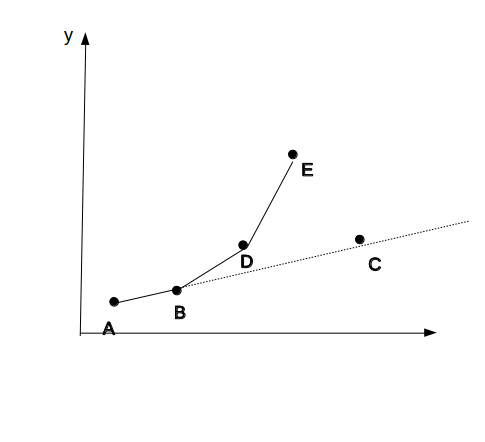
当B成为最优秀决策点的时候，那么根据前面两幅图的规律，我们应该队首弹出A点，而根据凸壳的规律后面的点点之间的线的斜率必然是在单调递增的，而至于后面的点因为相邻的点连线如\(BD,DE\)的斜率都会比\(AB\)大，而且根据注释中的本质知道这些直线必然都在C的上方，于是后面的点与C只能构成上凸三角形，前面的点总比后面优秀，暂时不会成为最有决策点，但根据前面归纳的性质，上凸三角形是有潜力变为上凸三角形的，于是单调队列中还要保存他们

于是总上所素，可以单调队列维护一个上凸壳，在队首根据上凸三角形和下凸三角形的性质决定谁是最优决策点，在队尾加入新的决策点，维护上凸壳的性质，每次算\(f_i\)时，直接取队首即可，于是可以做到\(O(n)\)。

参考代码：

#include <iostream>
#include <cstdio>
#define il inline
#define ri register
#define lb long double
using namespace std;
lb a[100001];
int T[100001],L,R;
template<class free>
il free Max(free,free);
int main(){
	int n,f;lb ans(-1e16);scanf("%d%d",&n,&f);
	for(int i(1);i<=n;++i)scanf("%Lf",&a[i]),a[i]+=a[i-1];T[L=R=1]=0;
	for(int r(f);r<=n;++r){
		while(L<R&&(a[T[L+1]]-a[T[L]])/(T[L+1]-T[L])<=(a[r]-a[T[L+1]])/(r-T[L+1]))++L;
		ans=Max(ans,(a[r]-a[T[L]])/(r-T[L]));
		while(L<R&&(a[T[R]]-a[T[R-1]])/
			  (T[R]-T[R-1])>=(a[r-f+1]-a[T[R]])/(r-f+1-T[R]))--R;
		T[++R]=r-f+1;
	}printf("%d",(int)(ans*1000));
	return 0;
}
template<class free>
il free Max(free a,free b){
	return a>b?a:b;
}