朴素贝叶斯算法

朴素贝叶斯分类方法

概率基础

概率(Probability)定义

• 概率定义为一件事情发生的可能性
  • 扔出一个硬币，结果头像朝上
  • 某天是晴天
• P(X) : 取值在[0, 1]

条件概率与联合概率

• 联合概率：包含多个条件，且所有条件同时成立的概率
  • 记作：P(A,B)
  • 特性：P(A, B) = P(A)P(B)
• 条件概率：就是事件A在另外一个事件B已经发生条件下的发生概率
  • 记作：P(A|B)
  • 特性：P(A1,A2|B) = P(A1|B)P(A2|B)

注意：此条件概率的成立，是由于A1,A2相互独立的结果(记忆)

贝叶斯公式

 

 那么这个公式如果应用在文章分类的场景当中，我们可以这样看：

 

 

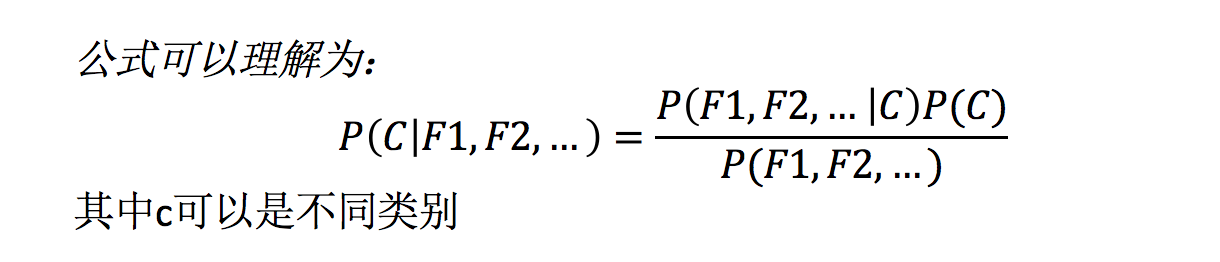
公式分为三个部分：

• P(C)：每个文档类别的概率(某文档类别数／总文档数量)
• P(W│C)：给定类别下特征（被预测文档中出现的词）的概率
  • 计算方法：P(F1│C)=Ni/N （训练文档中去计算）
    • Ni为该F1词在C类别所有文档中出现的次数
    • N为所属类别C下的文档所有词出现的次数和
• P(F1,F2,…) 预测文档中每个词的概率

如果计算两个类别概率比较：

 

 所以我们只要比较前面的大小就可以，得出谁的概率大

 

文章分类计算

假设我们从训练数据集得到如下信息

 

 

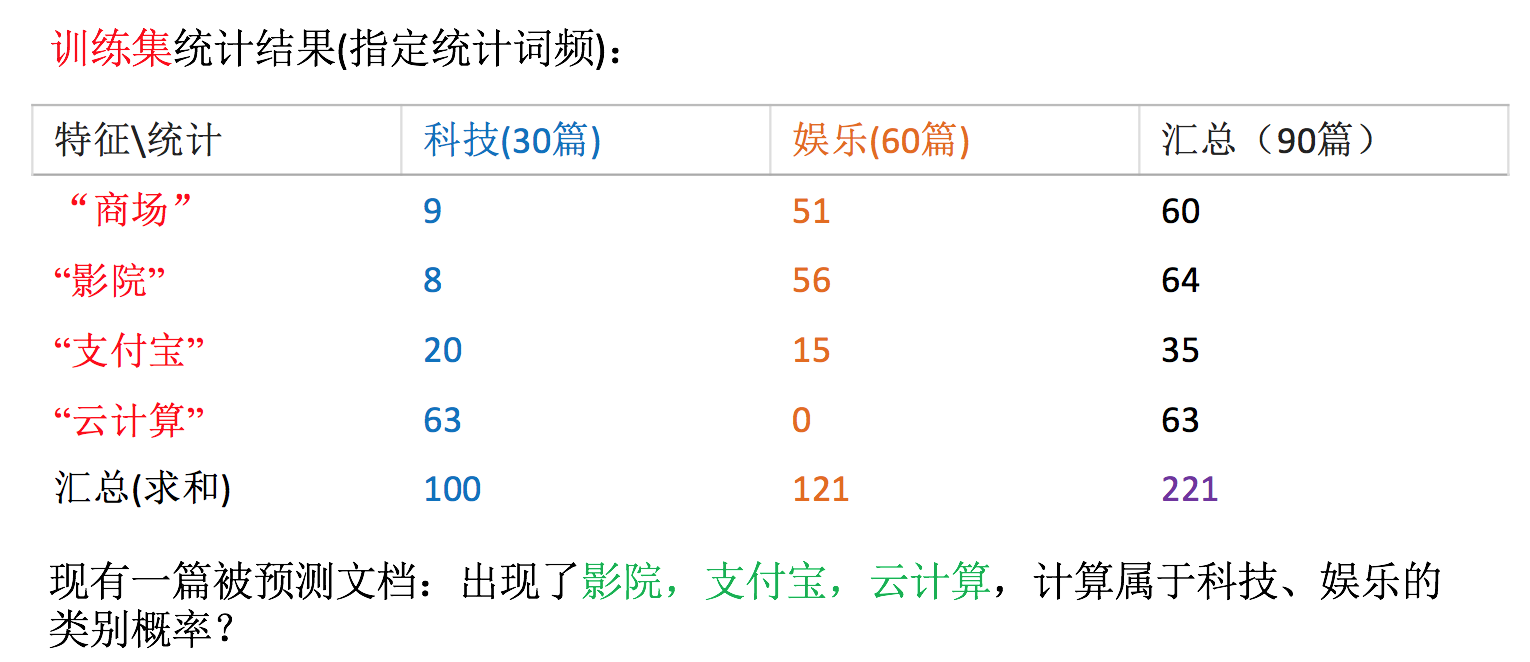
• 计算结果

科技：P(科技|影院,支付宝,云计算) = 𝑃(影院,支付宝,云计算|科技)∗P(科技)=(8/100)∗(20/100)∗(63/100)∗(30/90) = 0.00456109

娱乐：P(娱乐|影院,支付宝,云计算) = 𝑃(影院,支付宝,云计算|娱乐)∗P(娱乐)=(56/121)∗(15/121)∗(0/121)∗(60/90) = 0

思考:我们计算出来某个概率为0，合适吗？

拉普拉斯平滑系数

目的：防止计算出的分类概率为0

 

 

P(娱乐|影院,支付宝,云计算) =P(影院,支付宝,云计算|娱乐)P(娱乐) =P(影院|娱乐)*P(支付宝|娱乐)*P(云计算|娱乐)P(娱乐)=(56+1/121+4)(15+1/121+4)(0+1/121+1*4)(60/90) = 0.00002

API

sklearn.naive_bayes.MultinomialNB(alpha = 1.0)

• 朴素贝叶斯分类
• alpha：拉普拉斯平滑系数

案例：20类新闻分类

 

 

分析

• 分割数据集

• tfidf进行的特征抽取

• 朴素贝叶斯预测

代码：

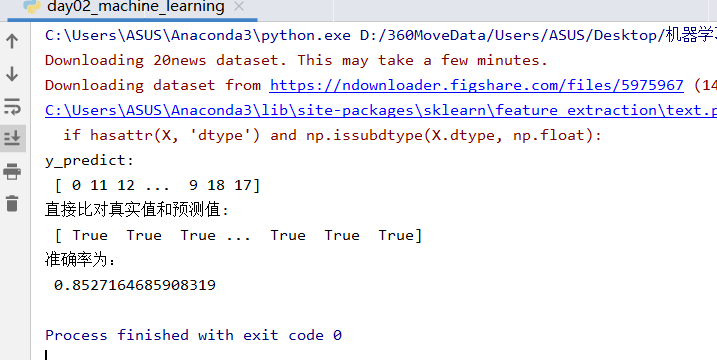
from sklearn.model_selection import train_test_split
from sklearn.datasets import fetch_20newsgroups
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.naive_bayes import MultinomialNB
def nb_news():
    """
    用朴素贝叶斯算法对新闻进行分类
    :return:
    """
    # 1）获取数据
    news = fetch_20newsgroups(subset="all")

    # 2）划分数据集
    x_train, x_test, y_train, y_test = train_test_split(news.data, news.target)

    # 3）特征工程：文本特征抽取-tfidf
    transfer = TfidfVectorizer()
    x_train = transfer.fit_transform(x_train)
    x_test = transfer.transform(x_test)

    # 4）朴素贝叶斯算法预估器流程
    estimator = MultinomialNB()
    estimator.fit(x_train, y_train)

    # 5）模型评估
    # 方法1：直接比对真实值和预测值
    y_predict = estimator.predict(x_test)
    print("y_predict:\n", y_predict)
    print("直接比对真实值和预测值:\n", y_test == y_predict)

    # 方法2：计算准确率
    score = estimator.score(x_test, y_test)
    print("准确率为：\n", score)

    return None
if __name__ == "__main__":
    # 代码3：用朴素贝叶斯算法对新闻进行分类
     nb_news()

 

总结

• 优点：
  • 朴素贝叶斯模型发源于古典数学理论，有稳定的分类效率。
  • 对缺失数据不太敏感，算法也比较简单，常用于文本分类。
  • 分类准确度高，速度快
• 缺点：
  • 由于使用了样本属性独立性的假设，所以如果特征属性有关联时其效果不好