汉诺塔

汉诺塔问题是一个经典的问题。汉诺塔（Hanoi Tower），又称河内塔，源于印度一个古老传说。

 汉诺塔问题分析:

 解决该问题分为三步1：将n-1个盘子的整体从A移动到缓冲区B中；

                                  2：接着将第n个盘子从A移动到C中;

                                 3：将n-1个盘子的整体从缓冲区B移动到C中。

如图所示: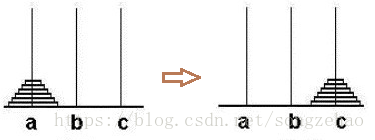

 

 

 

 

     算法1：

import turtle

class Stack:
def __init__(self):
self.items = []
def isEmpty(self):
return len(self.items) == 0
def push(self, item):
self.items.append(item)
def pop(self):
return self.items.pop()
def peek(self):
if not self.isEmpty():
return self.items[len(self.items) - 1]
def size(self):
return len(self.items)

def drawpole_3():#画出汉诺塔的poles
t = turtle.Turtle()
t.hideturtle()
def drawpole_1(k):
t.up()
t.pensize(10)
t.speed(100)
t.goto(400*(k-1), 100)
t.down()
t.goto(400*(k-1), -100)
t.goto(400*(k-1)-20, -100)
t.goto(400*(k-1)+20, -100)
drawpole_1(0)#画出汉诺塔的poles[0]
drawpole_1(1)#画出汉诺塔的poles[1]
drawpole_1(2)#画出汉诺塔的poles[2]

def creat_plates(n):#制造n个盘子
plates=[turtle.Turtle() for i in range(n)]
for i in range(n):
plates[i].up()
plates[i].hideturtle()
plates[i].shape("square")
plates[i].shapesize(1,8-i)
plates[i].goto(-400,-90+20*i)
plates[i].showturtle()
return plates

def pole_stack():#制造poles的栈
poles=[Stack() for i in range(3)]
return poles

def moveDisk(plates,poles,fp,tp):#把poles[fp]顶端的盘子plates[mov]从poles[fp]移到poles[tp]
mov=poles[fp].peek()
plates[mov].goto((fp-1)*400,150)
plates[mov].goto((tp-1)*400,150)
l=poles[tp].size()#确定移动到底部的高度（恰好放在原来最上面的盘子上面）
plates[mov].goto((tp-1)*400,-90+20*l)

def moveTower(plates,poles,height,fromPole, toPole, withPole):#递归放盘子
if height >= 1:
moveTower(plates,poles,height-1,fromPole,withPole,toPole)
moveDisk(plates,poles,fromPole,toPole)
poles[toPole].push(poles[fromPole].pop())
moveTower(plates,poles,height-1,withPole,toPole,fromPole)

myscreen=turtle.Screen()
drawpole_3()
n=int(input("请输入汉诺塔的层数并回车:\n"))
plates=creat_plates(n)
poles=pole_stack()
for i in range(n):
poles[0].push(i)
moveTower(plates,poles,n,0,2,1)
myscreen.exitonclick()

算法2.

public class Hanoilmpl

{

public void hanoi(int n, char A, char B, char C) {
if (n == 1) {
move(A, C);
} else {
hanoi(n - 1, A, C, B);//步骤1 按ACB数序执行N-1的汉诺塔移动
move(A, C); //步骤2 执行最大盘子移动
hanoi(n - 1, B, A, C);//步骤3 按BAC数序执行N-1的汉诺塔移动
}
}

private void move(char A, char C) {//执行最大盘子的从A-C的移动
System.out.println("move:" + A + "--->" + C);
}

public static void main(String[] args) {
Hanoilmpl hanoi = new Hanoilmpl();
System.out.println("移动汉诺塔的步骤：");
hanoi.hanoi(3, 'a', 'b', 'c');
}
}

1、对于第num个盘子的“汉诺移动”，都需要传入三个参数 盘子号num、开始柱from、借助柱with、目标柱to；
2、先把本次的from柱作为num-1个盘子的from柱，本次to柱作为num-1个盘子的with柱，本次的with柱作为num-1个盘子的to柱，对num-1个盘子进行“汉诺移动”；
3、再把本次的盘子从from柱移动到to柱；
4、然后，由于本次的盘子已经在to柱，而num-1个盘子全在with柱，所以需要把num-1个盘子从with柱借助于from柱移动to柱.

算法3,待学过数学结构的二叉树，可以用二叉树法进行汉诺塔的计算。

     二叉树的先序遍历、中序遍历、后序遍历、层序遍历四种遍历是所有树和图、所有非线性算法的基础和原理，必须牢牢掌握这四种算法的递归(层序遍历一般不递归)以及非递归；掌握不了这四种算法，就无法掌握高级的排序和查找，也无法学好下学期的算法课，写的程序就永远是入门的、线性的、低效率的。

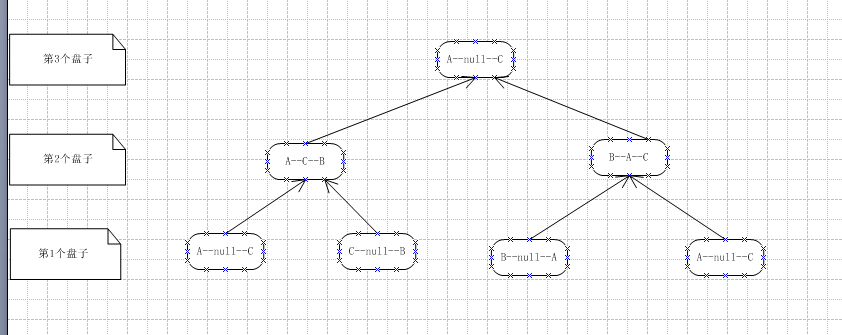
盘子:1A>>>>C
盘子:2A>>>>B
盘子:1C>>>>B
盘子:3A>>>>C
盘子:1B>>>>A
盘子:2B>>>>C
盘子:1A>>>>C
可以看到，汉诺塔算法所生成的二叉树是一个相当完美的“完全二叉树”，所以它的总节点数是2^3-1=7个。

最终得到执行结果：

老师，这次作业我真的尽力了，麻烦您给我一个比及格高一点的分数好不好。