Chapter1-逻辑语言

逻辑语言

逻辑域

最简单的论域

定义

逻辑对象是真和假，也称为逻辑真值，简称真值，记为 1 和 0

真值集合以及逻辑运算、逻辑关系统称为逻辑域

表达逻辑真值的变量，称为逻辑变量，简称变量

​ 一般用小写英文字母表示

由逻辑真值集合，逻辑运算集合以及关系集合构成的三元组成为逻辑域

• $\forall \exist \neg \wedge \vee, \rightarrow \leftrightarrow \oplus \models \vdash \Leftrightarrow \in \neq \equiv \cup \cap \infty $

符号表示

逻辑对象

​ \(\{ 0,1 \}\)

逻辑运算

​ \(\{ \neg ,\wedge ,\vee,\rightarrow,\leftrightarrow,\oplus \}\)

逻辑运算	符号
非	\(\neg\)
与	\(\wedge\)
或	\(\vee\)
如果...，则...	\(\rightarrow\)
当且仅当	\(\leftrightarrow\)
异或	\(\oplus\)

逻辑关系

​ \(\{ \Leftrightarrow , \models \}\)

真值表

​ 一组逻辑自变量与一个逻辑因变量的对应表

逻辑联结词

\(\neg\)

\(p\)	\(\neg p\)
1	0
0	1

\(\wedge\)

\(p\)	\(q\)	\(p\wedge q\)
0	0	0
0	1	0
1	0	0
1	1	1

\(\vee\)

\(p\)	\(q\)	\(p\vee q\)
0	0	0
0	1	1
1	0	1
1	1	1

$\rightarrow $

\(p\)	\(q\)	\(p\rightarrow q\)
0	0	1
0	1	1
1	0	0
1	1	1

sees as lambda x,y : x<=y

\(\leftrightarrow\) (互蕴含)

\(p\)	\(q\)	\(p\leftrightarrow q\)
0	0	1
0	1	0
1	0	0
1	1	1

sees as lambda x,y : x==y

\(p\leftrightarrow q = (p\rightarrow q) \wedge (q\rightarrow p)\)

\(\oplus\)

\(p\)	\(q\)	\(p\oplus q\)
0	0	0
0	1	1
1	0	1
1	1	0

\(p\oplus q = (p\wedge \neg q) \vee (\neg p \wedge q)\)

\(\Leftrightarrow\) (相等关系)

真值表，懒得写了

\(\models\) (推论关系)

\(p\)	\(q\)	\(p\models q\)
0	0	1
0	1	1
1	0	0
1	1	1

运算的性质

逻辑对象

\(\{ 0,1\}\)

逻辑运算

${ \neg ,\wedge , \vee , \rightarrow ,\leftrightarrow, \oplus} $

逻辑关系

${ \Leftrightarrow, \models} $

性质

• 结合律
• 交换律
• 分配律

合式公式

命题变量及原子公式

• 0 和 1 是常量
• 值取为逻辑真值的变量称为命题变量
  • 表示为小写字母 p, q, s, t 等

定义：命题变量称为原子公式

命题合式公式

定义

常量 0 和 1 是合式公式

命题变量是合式公式

若 Q, R 是合式公式，则 $(\neg Q) , (Q\wedge R) ,(Q\vee R) , (Q\rightarrow R ) , (Q\leftrightarrow R) ,(Q \oplus R) $ 是合式公式

只有有限次应用 (1)-(3) 构成的公式是合式公式

推断式

若 Q, R 是合式公式，则 \(Q\models R\) 是推论式

等价式

若 Q, R 是合式公式，则 \(Q\models R\) 是等价式

逻辑规律

定律与规则

• 思维直觉、思维定律与定理
• 充分理由律（三段论）： \(Q,Q\rightarrow R\models R\)
• 传递律： \(P\rightarrow Q, Q\rightarrow R \models P\rightarrow R\)
• 排中律： \(\models (Q\vee \neg Q)\)
• 矛盾律： \(\models \neg (Q\wedge \neg Q)\)

命题逻辑定理

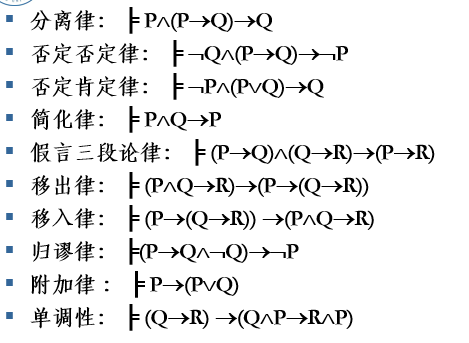
后面还一堆

??????

公式复杂度及合式公式序

公式 P 的复杂度表示为 \(FC(P)\)

常量 0, 1 复杂度为 0

命题变量复杂度为 0

如果 \(P = \neg Q\) ,则 \(FC(P) = FC(Q) +1\)

如果 \(P = Q\wedge R (\vee ,\rightarrow ,\leftrightarrow , \oplus)\) , 则 \(FC(P) = \max \{FC(Q),FC(R) \} + 1\)

联结词的优先级

从高到低： $\neg,\and ,\or ,\oplus ,\to, \leftrightarrow $

同一个联结词连续多次出现且无括号，则按照从左到右的顺序运算

在满足运算次序不变的情况下，运用联结词的优先级规则则可以减少合式公式括号。

命题逻辑语言

定义

所有的命题合式公式集合构成了命题逻辑语言，记为 \(\scr{L}_\mathnormal{p}\)

推论

一般来说，命题逻辑语言 $\scr{L}_\mathnormal{p} $ 是无穷集合，也就是说合式公式有无穷多个

等值演算

重要定律

交换律	\(Q\or R \Leftrightarrow Q\or R\)
结合律	\((P\or Q)\ or R \Leftrightarrow P\or(Q\or R)\)
分配律	\(P\or (Q\and R) \Leftrightarrow (P\or Q) \and (P\or R)\)
德·摩根律	\(\neg (Q\or R) \Leftrightarrow \neg Q\and \neg R\)
幂等律	\(Q \or Q\Leftrightarrow Q\)
同一律	\(Q\and 1 \Leftrightarrow Q\)
吸收律	\(Q\or(Q\and R) \Leftrightarrow Q\)
零律	\(Q\or 1 \Leftrightarrow 1\)
排中律	\(Q\or \neg Q \Leftrightarrow 1\)	双重否定律	\(\neg\neg Q \Leftrightarrow Q\)
矛盾律	\(Q\and \neg Q \Leftrightarrow 0\)	假言易位	\(Q\to R \Leftrightarrow \neg R\to \neg Q\)

等值演算

定义

设合式公式 \(Q, R\) ，存在等式序列 \(Q_0,\cdots,Q_n\) ，其中，$$