间断检测（二）

 高斯型的拉普拉斯算子

 　　LOG算子：是高斯和拉普拉斯的双结合，即集平滑和边沿于一身的算子模型！注意这个模型跟前面的一个滤波器很相似，就是各向异性滤波器！只不过是各向异性滤波器是高斯一阶导函数，而LOG可以看做是二阶导函数！这两个模型来源最初都是因为求导导致模板对噪声干扰敏感性比较强！

　　高斯卷积函数定义为：

                

 

 

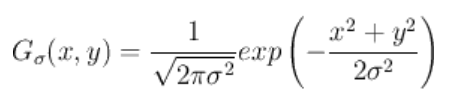
 　　而原始图像f(x,y) 与高斯卷积定义为：

                

 

　　而原始图像f(x,y) 与高斯卷积定义为：

 

               

 

 

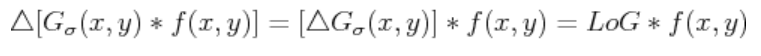
 因为：

              

 

 

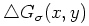
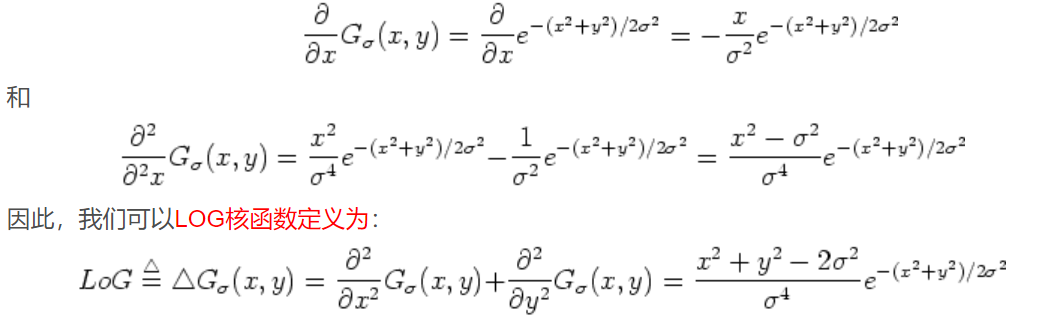
 　　所以Laplacian of Gaussian(LOG)可以通过先对高斯函数进行偏导操作，然后进行卷积求解。公式表示为：

           

 

 

 实例

color_pic=imread('lena.jpg');  %读取彩色图像
gray_pic=rgb2gray(color_pic);    %将彩色图转换成灰度图
double_gray_pic=im2double(gray_pic);   %将uint8转成im2double型便于后期计算
[width,height]=size(double_gray_pic);

noise_mean=0;  %添加均值为0
noise_var=0.01; %方差为0.001的高斯噪声
blur_noise=imnoise(double_gray_pic,'gaussian',noise_mean,noise_var);%添加均值为0，方差为0.001的高斯噪声
figure('name','运动模糊加噪');
subplot(1,2,1);imshow(double_gray_pic,[]);title('原图像');
subplot(1,2,2);imshow(blur_noise,[]);title('添加噪声');
Gau=fspecial('gaussian');
img_Gau=imfilter(blur_noise,Gau);
figure;
imshow(img_Gau);
title('高斯滤波之后');
model=[-1 -1 -1;-1 8 -1;-1 -1 -1];
result1=imfilter(blur_noise,model);
figure;
imshow(result1);
title('未进行高斯滤波后拉普拉斯');
result=imfilter(img_Gau,model);
figure;
imshow(result)
title('手动 LOG结果');

 

 

 

 

 

 

 

 　　下面采用内置函数：

color_pic=imread('lena.jpg');  %读取彩色图像
gray_pic=rgb2gray(color_pic);    %将彩色图转换成灰度图
double_gray_pic=im2double(gray_pic);   %将uint8转成im2double型便于后期计算
[width,height]=size(double_gray_pic);

noise_mean=0;  %添加均值为0
noise_var=0.01; %方差为0.001的高斯噪声
blur_noise=imnoise(double_gray_pic,'gaussian',noise_mean,noise_var);%添加均值为0，方差为0.001的高斯噪声
figure('name','运动模糊加噪');
subplot(1,2,1);imshow(double_gray_pic,[]);title('原图像');
subplot(1,2,2);imshow(blur_noise,[]);title('添加噪声');
Gau=fspecial('laplacian');
img_Gau=imfilter(blur_noise,Gau);
figure;
imshow(img_Gau);
title('拉普拉斯变换');
Gau=fspecial('log');
img_Gau=imfilter(blur_noise,Gau);
figure;
imshow(img_Gau);
title('高斯型的拉普拉斯算子');