膨胀与腐蚀

形态学处理

　　首先，我们来介绍一下形态学图像处理：

• 数学形态学的语言是集合论，它为大量的图像处理问题提供了一种一致的有力方法。
• 数学形态学中的集合表示图像中的不同对象。例如，在二值图像中，所有黑色像素的集合是图像完整的形态学描述。
• 在二值图像中，正被讨论的集合是二维整数空间（z^2）的元素，在这个二维整数空间中，集合的每个元素都是一个多元组，是一个黑色（或白色，取决于事先的约定）像素在图像中的坐标 (x, y)。

集合论的几个基本概念

令 A 为一个 z2 中的集合。

• 如果 a = (a1, a2) 是 A 的元素，则我们将其写成 a∈A；如果不是 A 的元素，则写成：a ∉A。

• 集合由两个大括号之中的内容表示，例：C = {w|w=-d, d∈D}

• 如果集合 A 的每个元素又是另一个集合 B 的一个元素，则 A 称为 B 的子集，表示为：A ⊆ B

• 两个集合 A 和 B 的并集表示为：C = A Ս B

• 两个集合 A 和 B 的交集表示为：D = A Ո B
  
  

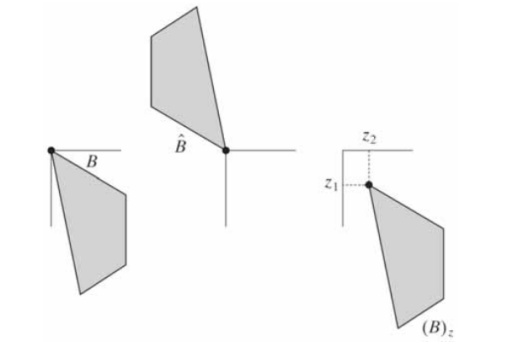
　　集合 B 的反射，表示为     ，定义为：

           

 

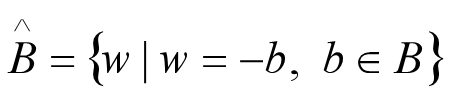
 　　集合 B 平移到点 z = (z1, z2)，表示为 (B)z，定义为：

           

 

 

 

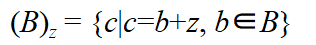
 膨胀

　　由于 A 和 B 是 z2 中的集合， A 被 B 膨胀定义为：

                

 

 

 

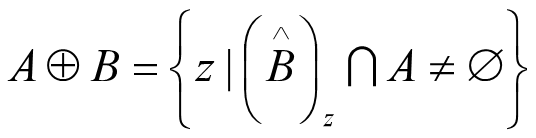
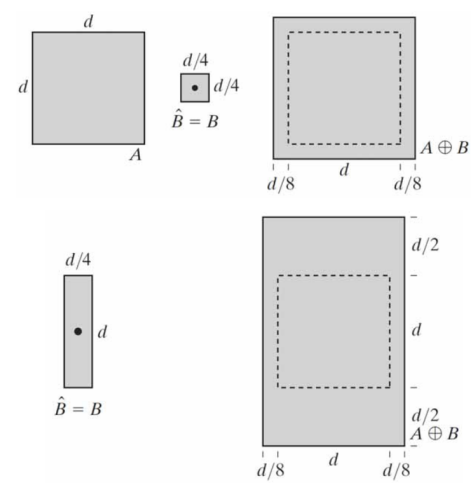
 代码

clear;clc;
width=500; %图像的宽
height=500; %图像的高
expand_size=200;

img=ones(width,height);
expand_img=double(wextend('2D','zpd',img,expand_size));%扩展0，也就是增加padding
model=ones(51,51);%模板大小为15
model_size=51;
cen=floor((model_size+1)/2);

[M,N]=size(expand_img);
img_result=zeros(M,N);
for i=1:(M-model_size)
for j=1:(N-model_size)
ave=sum(sum(expand_img(i:i+model_size-1,j:j+model_size-1).*model));
if ave>0
img_result(i+cen,j+cen)=255;
end
end
end
figure
subplot(1,2,1);
imshow(expand_img)
title('原图像');
subplot(1,2,2);
imshow(img_result)
title('膨胀之后的图像');

　　本例中采用结构元50*50：

 

 腐蚀

　　对 z^2 中的集合 A 和 B， 使用 B 对 A 进行腐蚀， 定义为：

                 

 

 

 

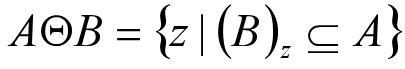
代码

clear;clc;
width=500;  %图像的宽
height=500;  %图像的高
expand_size=200;

img=ones(width,height);
expand_img=double(wextend('2D','zpd',img,expand_size));%扩展0，也就是增加padding
model=ones(51,51);%模板大小为51
model_size=51;
cen=floor((model_size+1)/2);
Sum=model_size*model_size;

[M,N]=size(expand_img);
img_result=zeros(M,N);
for i=1:(M-model_size)
    for j=1:(N-model_size)
        ave=sum(sum(expand_img(i:i+model_size-1,j:j+model_size-1).*model));
        if ave==Sum
            img_result(i+cen,j+cen)=255;
        end
    end
end
figure
subplot(1,2,1);
imshow(expand_img)
title('原图像');
subplot(1,2,2);
imshow(img_result)
title('腐蚀之后的图像');