几何之敌—作图

作图题通常是同学们大脑宕机的转折点。想不到怎么做？这次，就带你理清大考中出现的一些作图题，并找出它们之间的关联，从而做到举一反三，轻松秒杀作图题。

单规作图

圆规能做的实在有限。划弧，截长，相交。仅仅只能做这三点。而单规作图要做的，就是利用这三点，画出求作的图形。

单规作平行

单规作矩形

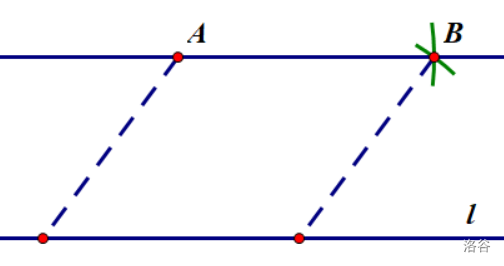
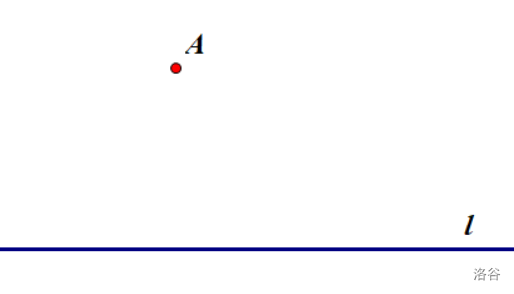
样题：如图，直线\(l\)上方有一点\(A\)。仅利用圆规作图。

\((1)\)作点\(B\)，使\(AB\parallel l\)。

\((2)\)作点\(B\)、\(C\)、\(D\)，使四边形\(ABCD\)为矩形。

题目内容很强劲，读完大脑未响应。

第一题，简单，只要学过四边形：

第二题，……说实话我第一眼看到这道题的时候也懵了。
矩形？什么要求也没有？单规也做不出矩形啊！

此时，我们就要灵活运用那条\(l\)。

“没有无缘无故的爱，也没有无缘无故的恨，更没有无缘无故的第一小问。”——吴岳衡传世名言

那我们就保持\(AB\parallel l\)不变吧，正好\(B\)可以用作一个顶点。

等等！既然\(A\)、\(B\)都出来了，那岂不是要保证\(AC⊥AB\)或者\(AC⊥BC\)了？这该怎么办啊！
此时你就应该想到，要做垂直，就要……

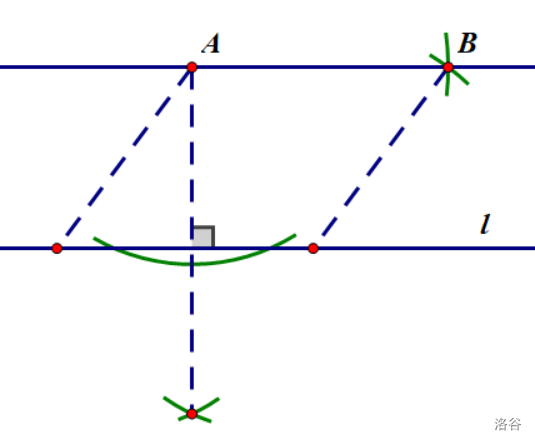
哦哦哦！单规作图恰好能作出一个\(C\)点使得\(AC⊥AB\)！
那么接下来，就顺理成章了吧？

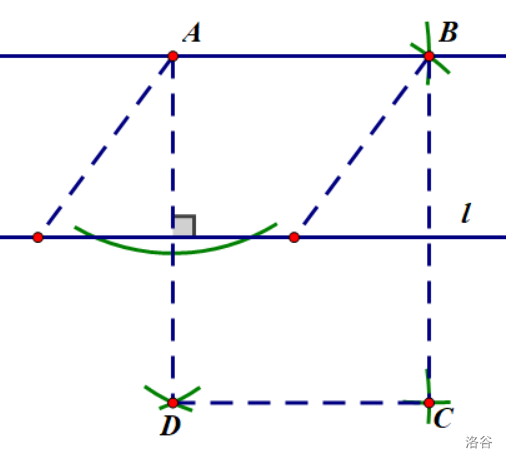
注：为了字母对应，这里把\(C\)、\(D\)对应。

单规作图的题目实在太少了，要么就要用圆和相似……这道题目可以说是初二单规作图出得最好的一道题。单规没有什么普遍规律可以总结，引理也很散，因此一般较难。初三学习了圆和相似以后，单规作图会变得更难。

\(1797\)年，意大利数学家马歇罗尼在其著作《圆规几何学》中证明得出了一个有趣的结论：

凡是尺规作图能够做出的点，仅使用一把圆规均可做出。而尺规作图的本质就是做出特定点，由此得出，尺规作图与单规作图等价。

这一结论被后人称为“摩尔—马歇罗尼定理”。

单尺作图

单尺作图分为：有刻度直尺作图和无刻度直尺作图。在以后的标题中，它们分别以\(G(graduated)\)和\(U(ungraduated)\)呈现。

（\(G\)）单尺作平行

方老师特供。

首先看到平行，你应该想到，你可以用什么方法构造平行。这和我们常规的说法，即画出效果图—反推或削弱条件—作图是不一样的，因为对这道题目来说，画出效果图并不能帮到你什么。

显而易见，在你现在的学习范围内，有且只有四样东西可以构造平行：

平行四边形；
中位线；
平行—中点—八字全等；
三线八角。

你可以立刻排除的是选项\(4\)，因为它仅和角有关，并且用单尺是做不出任何有条件的角的。
你第二个可以排除的是选项\(1\)，因为构造平行四边形只能做两组对应边相等。（对角线除外，那和选项\(3\)重复。）而你无法保证做出来的两组对应边的末端恰好重合。
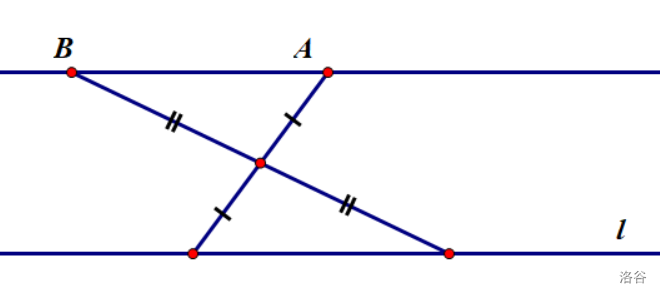
留给你的只有中位线和平行—中点—八字全等。事实上，这两种方法都可以。

我首先想到的其实是正\(A\)字相似，但中位线其实是相似的一种特殊情况。

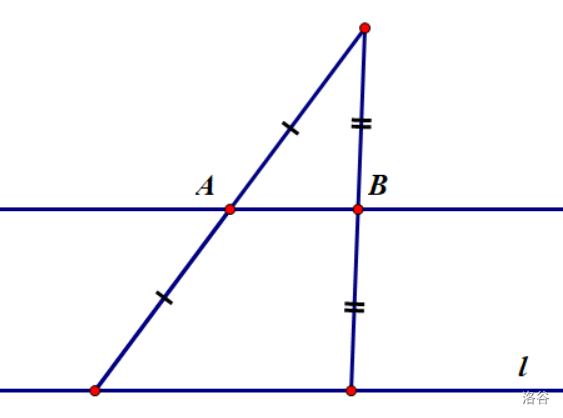
另外一种方法其实只是把中位线向内凹了一下。

硬广：

更多关于单尺作图的详细信息，请咨询贝爷（吴岳衡）。

尺规作图

在尺规作图界有一个广为流传的法则，叫“尺规五大基本作图”。我曾经在提优班的讲义上详细了解过，得以在此献给各位读者。

尺规五大基本作图

它们分别是：

复制线段

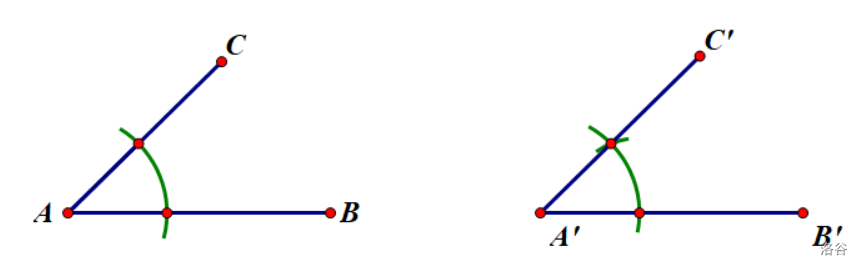
复制角

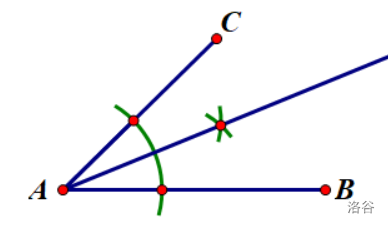
作角平分线

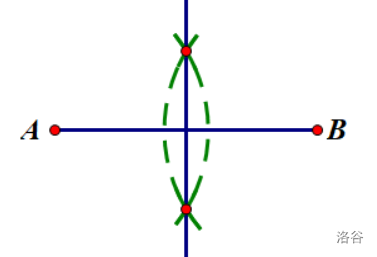
作垂直平分线（\(中垂线\)）

作垂线

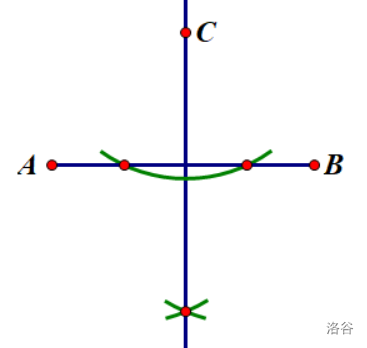
当年，这号称是任何的尺规作图题都可以拆分成五种基本作图。不过在我看来，那只能是较为简单的尺规作图的解法。看看历年来中考以及期末统考的尺规作图题目，就可以感受到下面这句话的正确性。

尺规作图没有下限，更没有上限。

\(2025\)—南京

过直线外一点作已知直线的平行线。

\[??? \]

好像也是哦，作平行线确实不是基本作图🤣。
根据\(两直线平行，内错角相等\)解答即可。

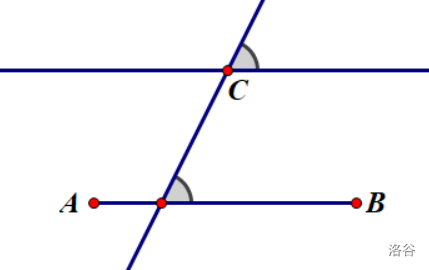
也可另辟蹊径，使用平行四边形相关知识作答。依据是\(两组对边分别相等的四边形是平行四边形\)和\(平行四边形的对边平行\)。

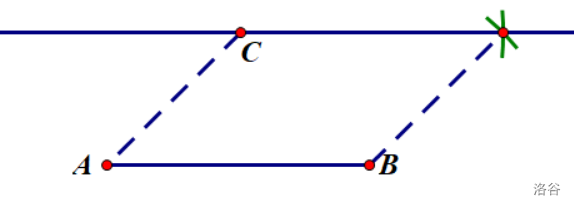
简洁凝练，不拖泥带水。说实话，如果那两条虚线不连，改卷老师就会后悔没让考生写必要的文字说明。

因此，我们似乎可以从这道题中看出，尺规作图在出题人眼中的影响力在逐渐下滑。不过我们不能妄下定论，毕竟\(2026\)届中考可就不好说了……

\(2024\)—南京

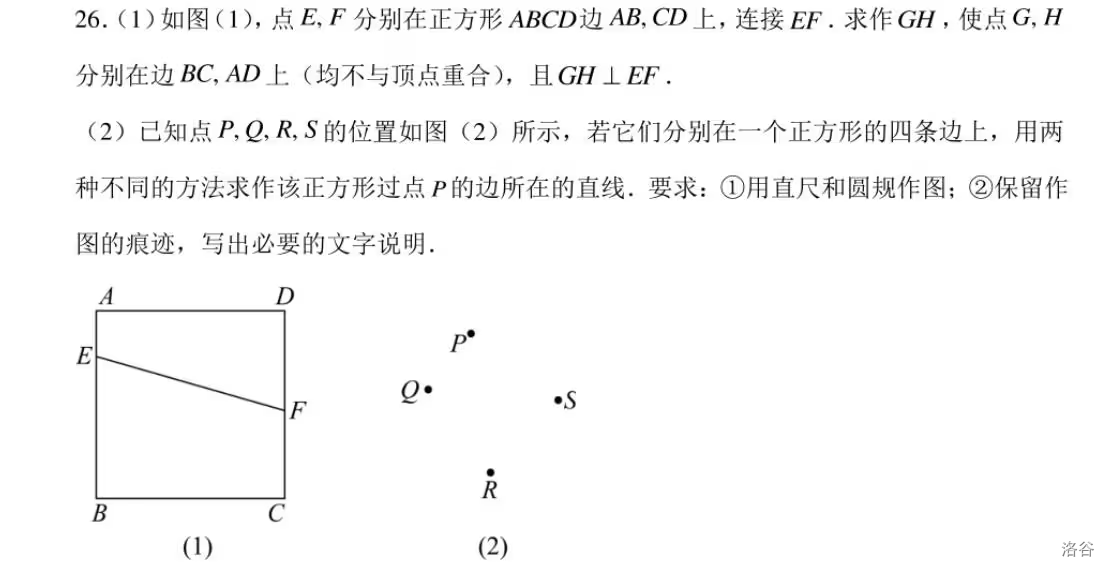
这道题应该已经十分熟悉了吧，我们先把常规方法展示一下。

\((1)\)解析略。

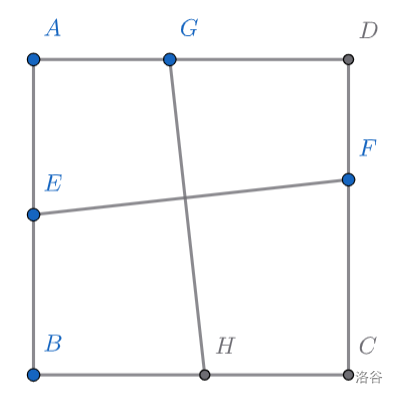
\((2)\)受第\((1)\)小问启发，方法1使用\(十字架模型\)相等—垂直的结论解题。（这里没有使用相等→垂直是因为有情况存在，\(EF=GH_1\)但不垂直。）

如图，直线\(l\)即为所求。

网上还有作圆法作为方法2，可惜我不会，大多数人也不会，因此我闭口不谈。

不过！我说还有第三种方法，你信吗？

第三种方法需要思路转一转。首先，\(十字架模型\)的根本是不是作出垂直？那作出垂直还有什么方法呢？
正方形内两条边既相等又垂直，那么它的……

中点四边形就是正方形。

漂亮，我们又想出了一种~~混分的~~方法。

实现也很简单，连接三个顶点，作正方形（即为四边形\(PQRT\)的中点四边形），然后把四边形\(PQRT\)补全即可。作图痕迹如图。

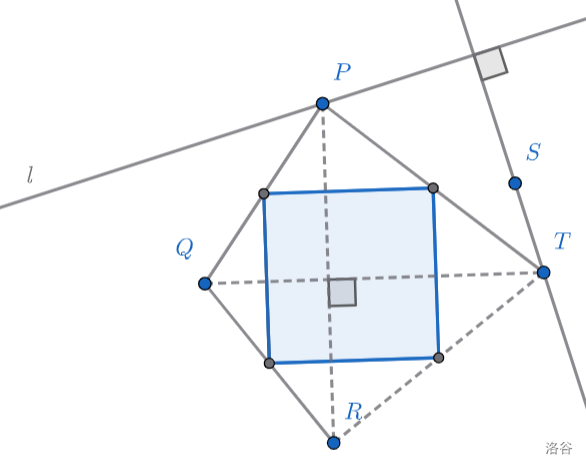
怎么样，辅助线都画好了，中间的蓝色四边形是正方形。其实就是变相作了个垂直必相等。

我们得出结论，至少对于这类题目来说，熟练掌握模型十分重要。

2023年南京没考尺规作图。

\(2022\)—南京（这考了个啥？）

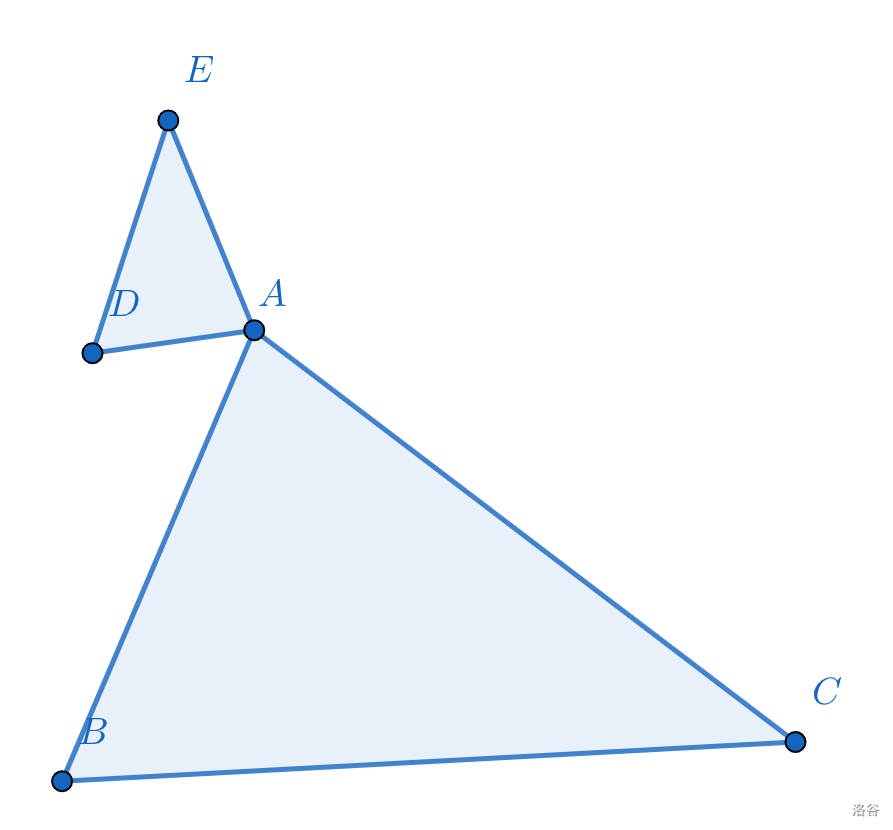
在平面内，先将一个多边形以自身的一个顶点为位似中心放大或缩小，再将所得多边形沿过该点的直线翻折，我们称这种变换为自位似轴对称变换，变换前后的图形成自位似轴对称。例如：如图\(1\)，先将\(\triangle ABC\)以点\(A\)为位似中心缩小，得到\(\triangle ADE\)，再将\(\triangle ADE\)沿过点\(A\)的直线\(l\)翻折，得到\(\triangle AFG\)，则\(\triangle ABC\)和\(\triangle AFG\)成自位似轴对称。

\((2)\)如图\(3\)，已知\(\triangle ABC\)经过自位似轴对称变换得到\(\triangle ADE\)，\(Q\)是\(DE\)上一点。用直尺和圆规作点\(P\)，使点\(P\)与\(Q\)是该变换前后的对应点。（保留作图痕迹，写出必要的文字说明。）

什么？位似？我不会啊。
若两个相似的图形对应点连线所在直线交于同一点，则称这两个图形位似（\(homothetic\)）；这个点称为两个图形的位似中心（\(homothetic\ centre\)）。

什么？相似？我不会啊。

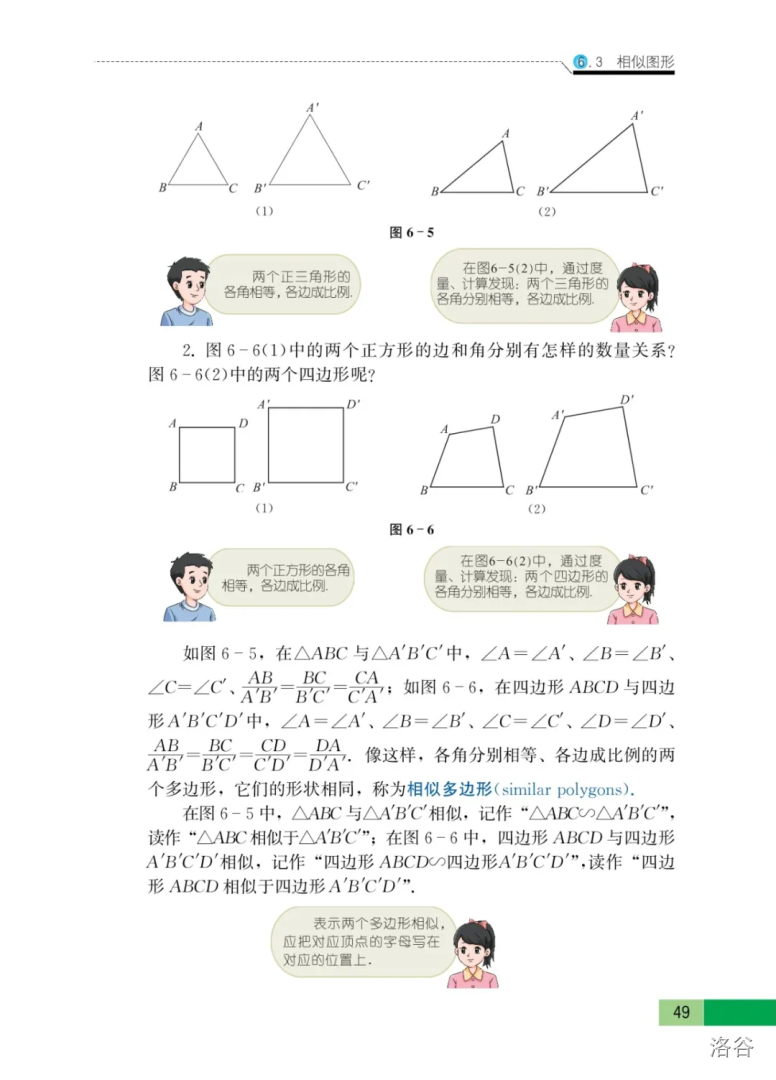
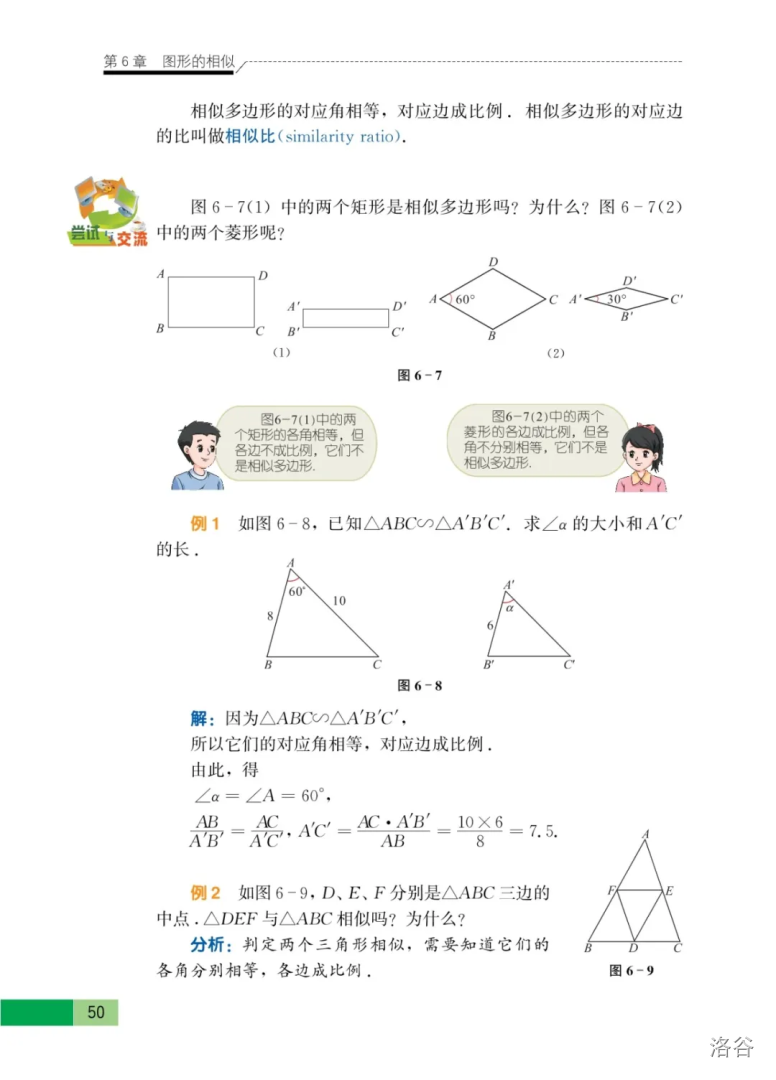
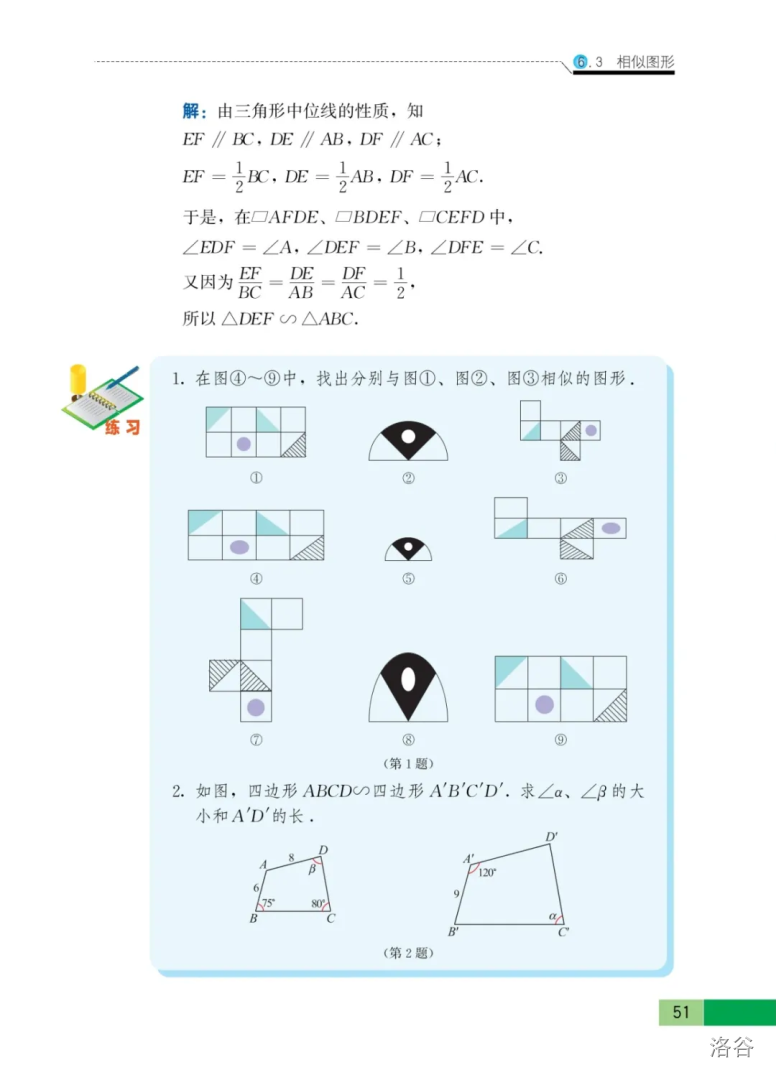
如果到这里你还没有放弃，那么恭喜你，打败了……一大部分同学。当然，如果你觉得相似太难了，那当然没问题，可以跳过此题，在预习或学习完后再看看。

要解此题，需要用到的重要模型是正\(A\)字相似。当然，这个是校内必背模型之一，又称平行出相似。（对！就是期末考试\(T16\)😂！）

如果你已经熟悉该模型，请移步至下一个分割线处。

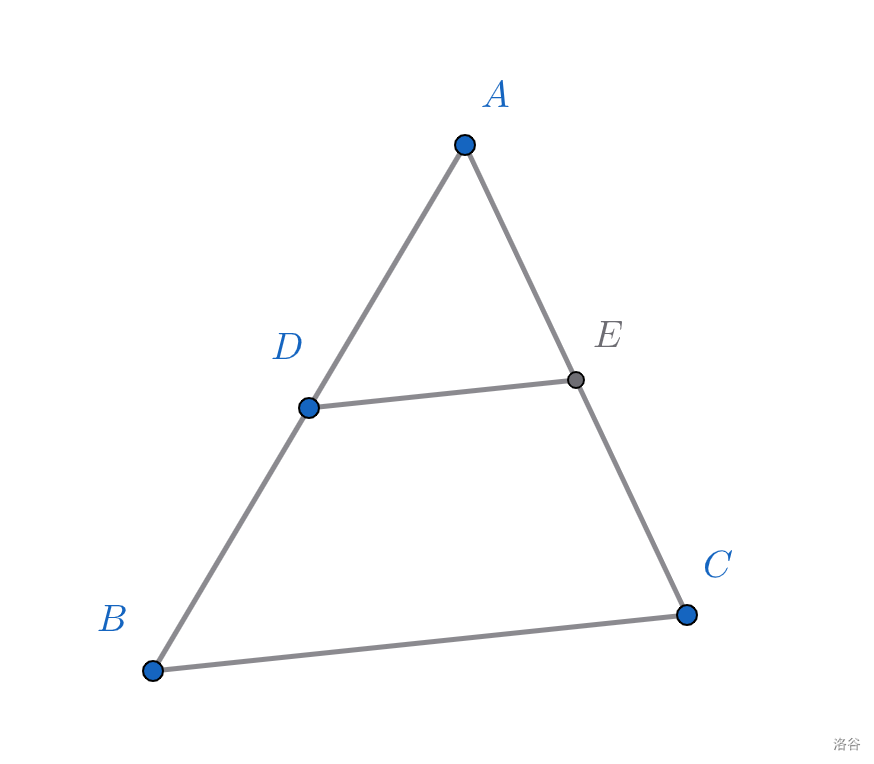
免责声明：以后的\(\sim\)符号，一律读作\(相似于\)。该符号在不同数学领域和地域有不同写法，我国规定\(相似于\)写作\(∽\)，而有其它地区写作\(\sim\)。很遗憾的是，\(LaTeX\)公式（这是主播写文稿用的公式语言，不必了解）只为\(相似于\)符号保留了\(\sim\)写法，在此感到抱歉。类似地，以后\(全等于\)符号写作\(\cong\)，规范写法是\(≌\)！

再次声明：\(相似于\)符号写作∽或\(∽\)；\(全等于\)符号写作≌或\(≌\)！

如图，\(\triangle ABC\sim \triangle ADE\)，\(D\)、\(E\)分别在\(AB\)、\(AC\)上，你能否得出某些结论呢？

根据\(相似图形对应角相等\)，可以得出\(\angle ADE=\angle ABC\)，进而得到\(DE\parallel BC\)。
同时，根据\(相似图形对应边成比例\)，可得\(\frac {AD} {AB}=\frac {AE} {AC}=\frac {DE} {BC}\)。

三个条件，知一推二。
对于第三个条件，知\(AD,AE\)和\(AB,AC\)成比例，可推其二。知其它两种组合成比例则不可。

证明：（选阅自取）

\((1)\)已知\(\triangle ABC\sim \triangle ADE\)，求证\(DE\parallel BC\)和\(\frac {AD} {AB}=\frac {AE} {AC}=\frac {DE} {BC}\)。

根据\(相似图形对应边成比例，对应角相等\)证明即可。

\((2)\)已知\(DE\parallel BC\)，求证\(\triangle ABC\sim \triangle ADE\)和\(\frac {AD} {AB}=\frac {AE} {AC}=\frac {DE} {BC}\)。

\[\because DE\parallel BC \]
\[\therefore \angle ADE=\angle B, \angle AED=\angle C \]
\[又\because \angle A=\angle A \]
\[\therefore \triangle ABC\sim \triangle ADE\ (AA) \]
这里的\(AA\)是三角形相似的条件，你可以理解为，三个角都相等的两个三角形相似，这很合理吧？

\[\therefore \frac {AD} {AB}=\frac {AE} {AC}=\frac {DE} {BC} \]
\((3)\)已知\(\frac {AD} {AB}=\frac {AE} {AC}\)，求证\(\triangle ABC\sim \triangle ADE\)和\(DE\parallel BC\)。

\[\because \frac {AD} {AB}=\frac {AE} {AC}, \angle A=\angle A \]
\[\therefore \triangle ABC\sim \triangle ADE\ (SAS) \]
类比全等，就可得到相似的另一种证明方法：\(SAS\)。

接下来，我们对不成立的两种情况举反例。

首先，对于\(AD,AE\)和\(DE,BC\)成比例，反例如图：

自然地，对于另一种情况，反例即为：

没想到吧，在哪儿都能碰见\(SSA\)。

你猜为什么我把三角形歪了一下？这就是因为在我刚刚画的那个条件下，\(\angle A>\angle D\)，\(SSA\)是成立的。（你没有忘记八年级上学期第二周周测的最后一题的最后一空吧？就是\(\angle B>\angle A或\angle B+\angle C=90\degree\)）

这模型还有个奇妙之处，就是过\(A\)点作任意一条直线交\(DE\)、\(BC\)于\(F\)、\(G\)，则又分辟出两个小\(A\)字，容易发现同样适用上述的结论。

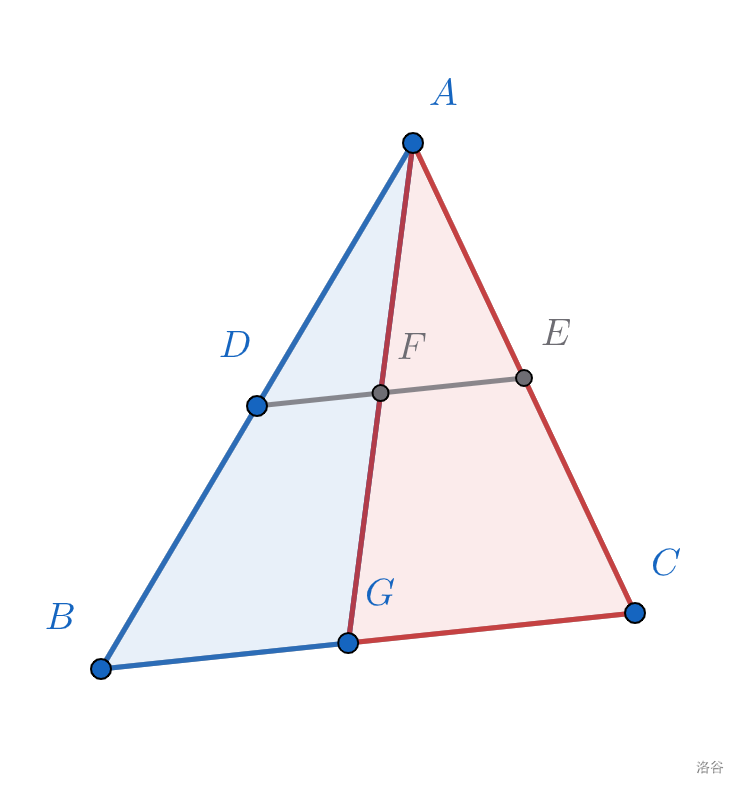
话休叙繁。且说那正\(A\)字模型为解此题之高妙处，何以见哉？观察题目给出的图\(1\)。

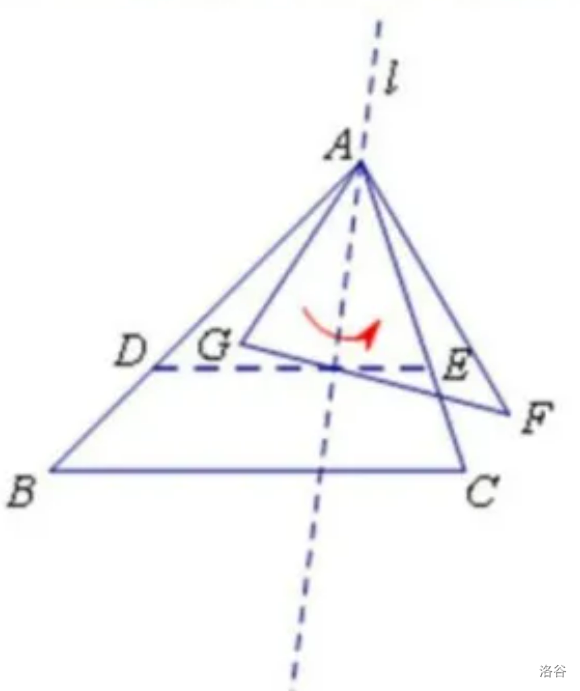
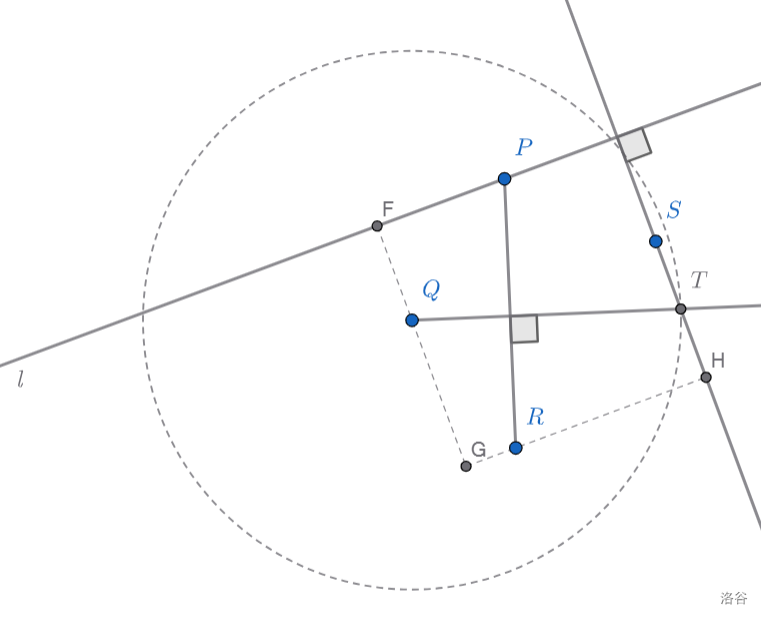
这题目中的\(\triangle ABC\)与\(\triangle ADE\)，说是位似，岂不就是相似出平行么？再回到我们做尺规作图的三步走，即：

\[画出效果图—反推或削弱条件—作图 \]

先把效果图画出来。

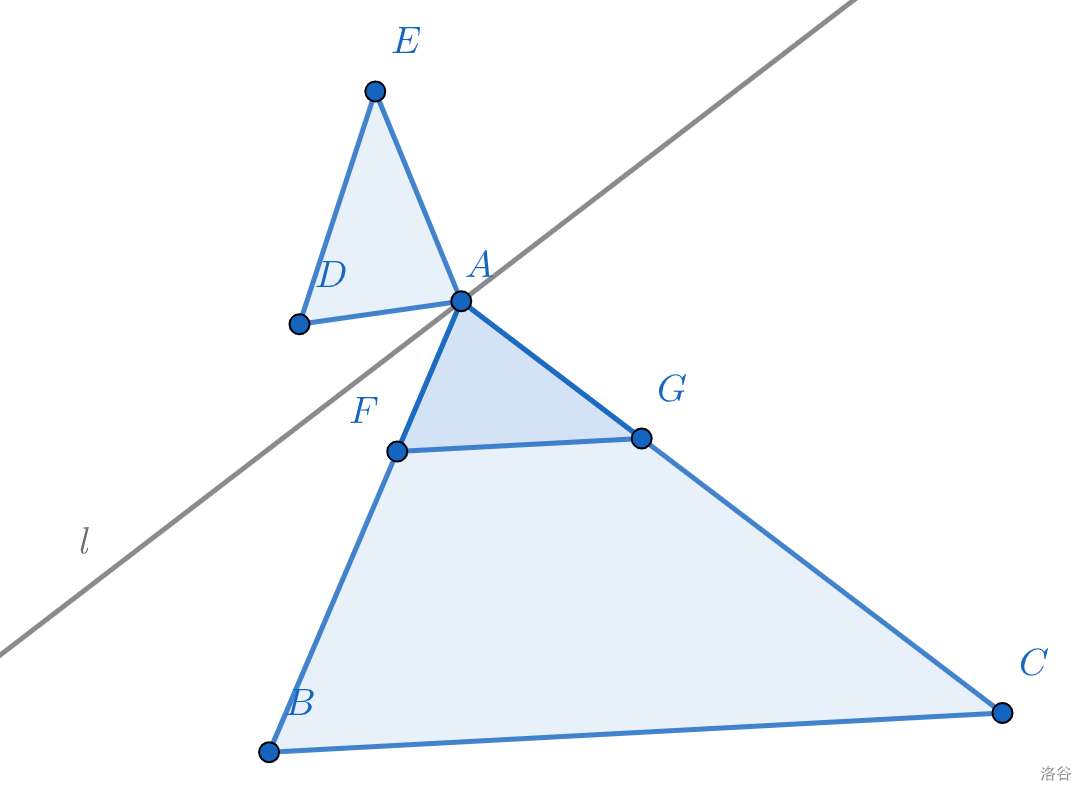
~~我\(1\)秒钟就画好了。~~
第二步，反推。

很显然，\(\triangle AFG\)和\(\triangle ADE\)关于\(l\)对称，而此题关键就是作出\(\triangle AFG\)和\(l\)。
根据\(轴对称的性质\)，连\(EG\)交\(l\)于点\(H\)，有\(AE=AG\)。因为\(l垂直平分EG\)，所以\(\angle EAH=\angle GAH\)。

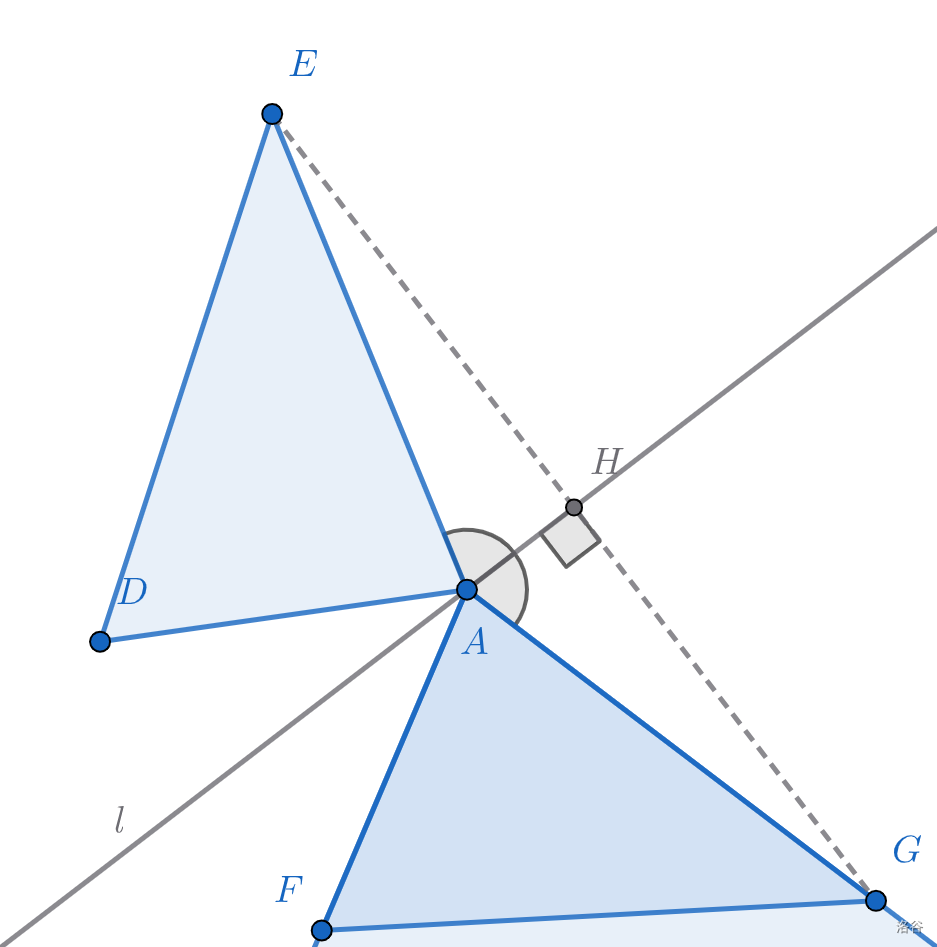
因此，关键就是作\(\angle EAC\)的平分线，即为\(l\)。

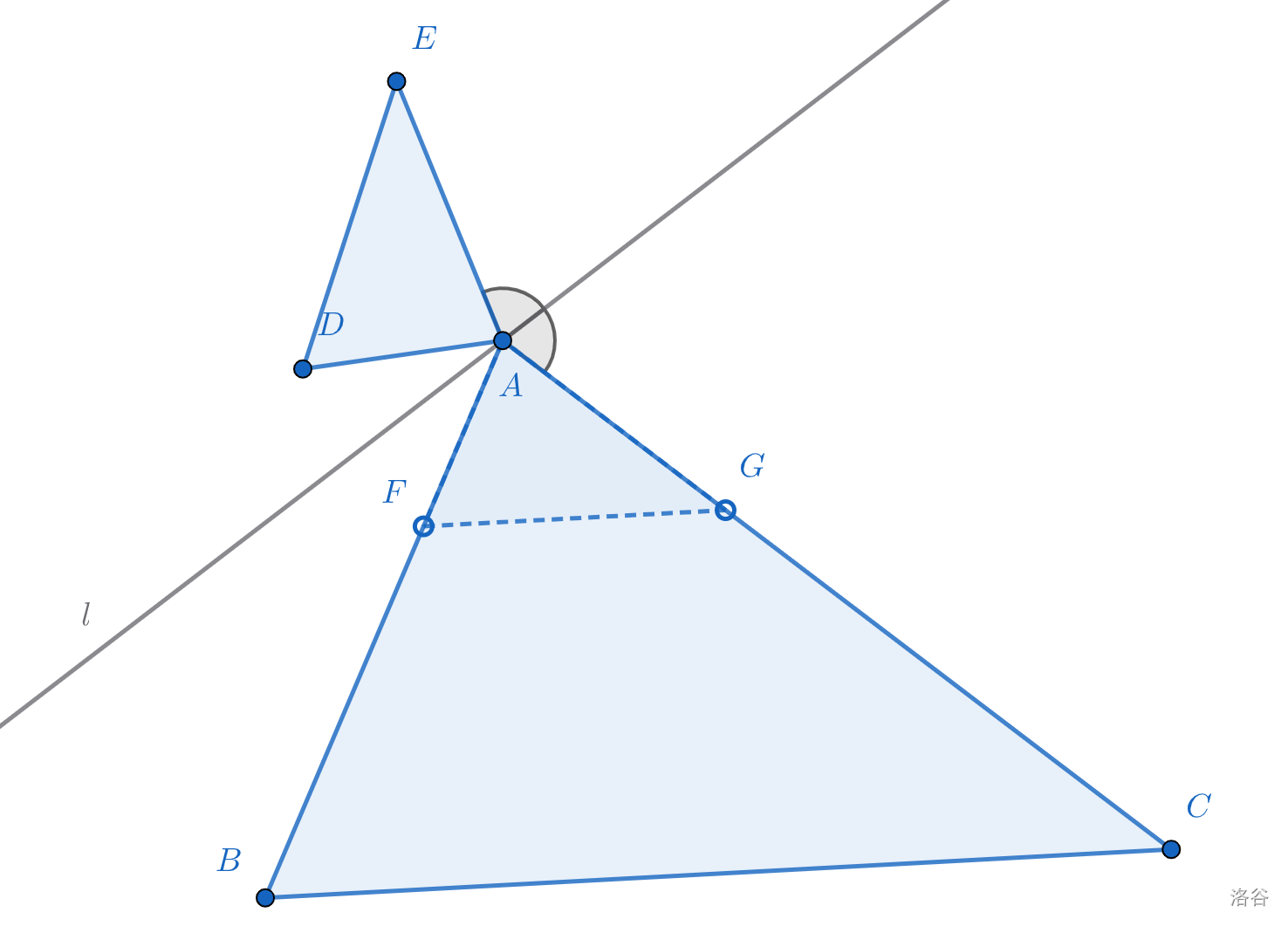
总感觉少了点什么……哦，少了个\(Q\)点，补上。
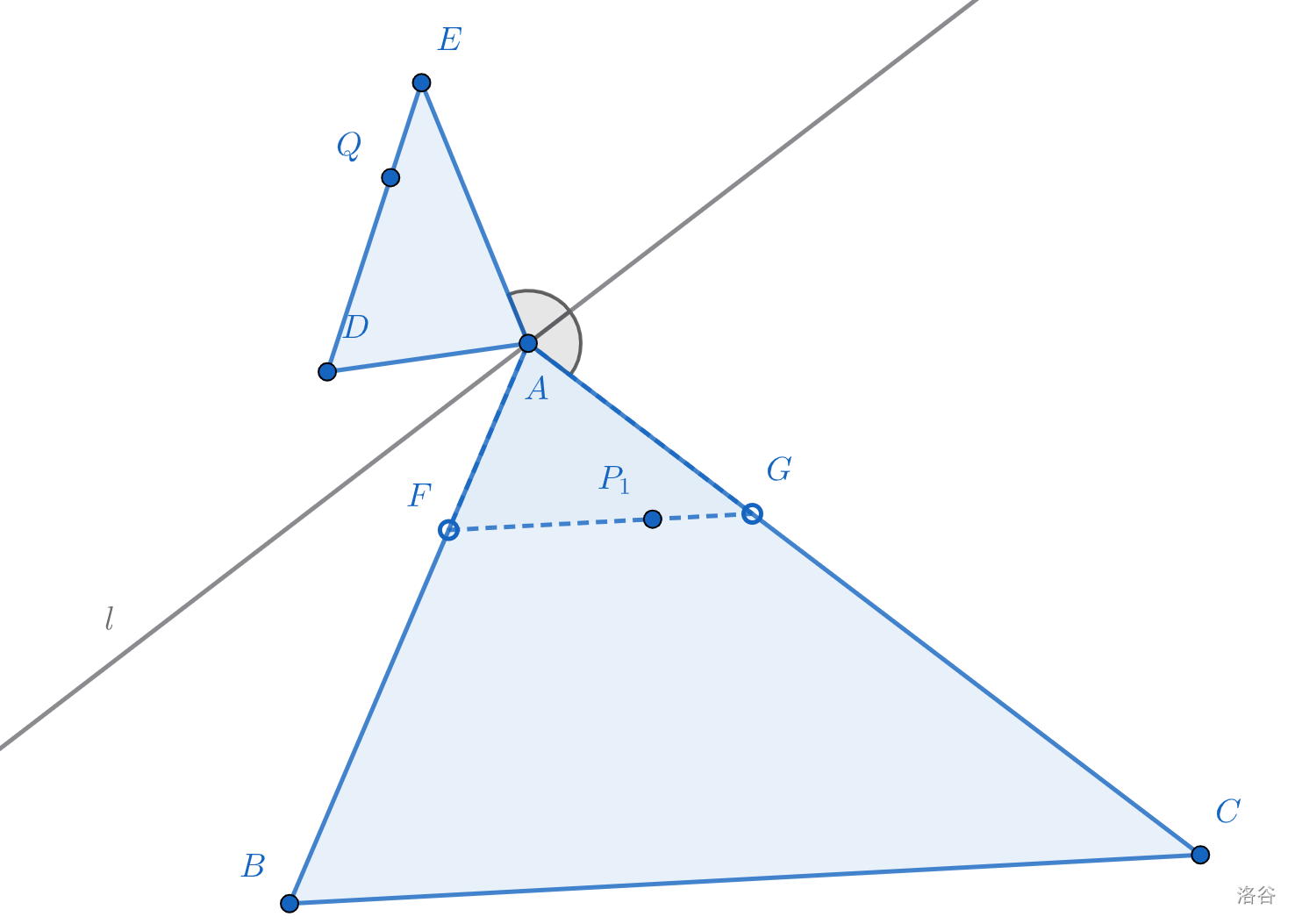
\(Q\)点补上了，那对称一下，\(P_1\)不就来了吗？

接下来，根据\(正A字模型分割理论\)，直接把\(AP_1\)延长下去交\(BC\)于\(P\)点即为所求。因为\(\triangle AFP_1\sim \triangle ABP\)，可以推出\(P\)与\(P_1\)一定是对应点。

一道“超纲”的题目就这样被我们做了出来。

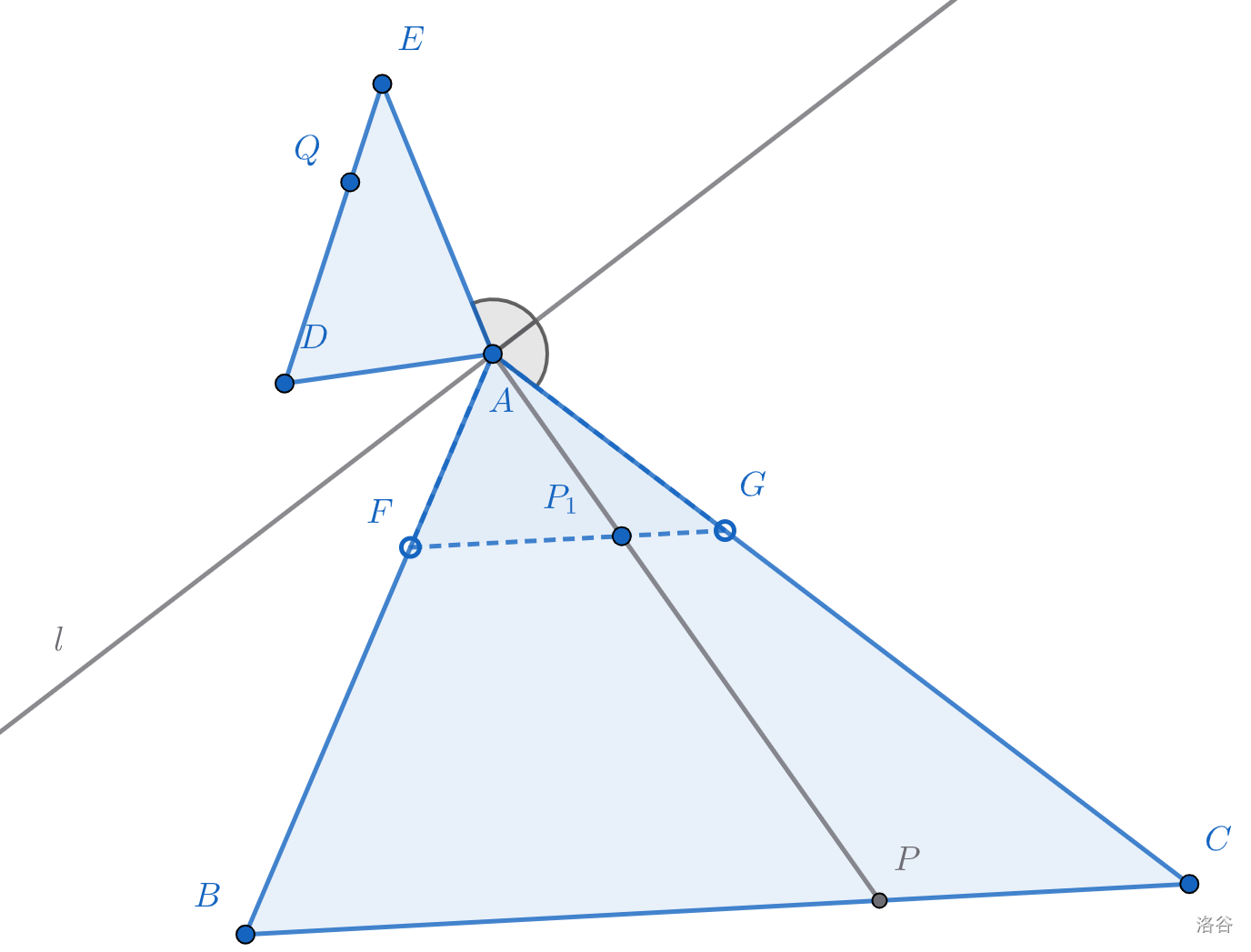
因此，我们得出，尺规作图三步走可以帮助我们想出大多数题目的作图思路。