第九单元：压强与浮力问题分类探究

压强与浮力是八年级下册最大的重难点。以下是常见的几类考法，且基本是二档题或三档题。

备注：物理题目基本可以分为四类。

类型	描述
一档题（基操题）	只需要一步即可解出。
二档题（中档题）	需要二到三步才能解出。
三档题（高档题）	需要四到六步，属于区统考最后一题难度。
四档题（竞赛题）	*&^%$#@!

固体压强

切切切问题

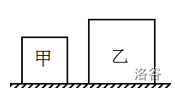
如图所示，实心均匀正方体甲、乙置于水平地面上，它们对地面的压强相等。现将它们沿竖直或水平方向切下质量相同的一部分，并将各自切下部分叠放在对方剩余部分的上表面中央，此时它们对水平地面的压强分别为\(p_甲\)、\(p_乙\)。下列说法中正确的是：

A. 若甲竖直切，乙水平切，则\(p_甲\)一定大于\(p_乙\)。
B. 若甲水平切，乙竖直切，则\(p_甲\)可能等于\(p_乙\)。
C. 若甲、乙均水平切，则\(p_甲\)一定大于\(p_乙\)。
D. 若甲、乙均竖直切，则\(p_甲\)可能等于\(p_乙\)。

此类切切切问题可以说是固体压强考查的极限了。解此类问题的策略就是耐心分析，列出等量关系和不等关系。

首先，读到“压强相等”，你应该列出：

\[p_甲=p_乙 \]

\[ρ_甲>ρ_乙（由h_甲<h_乙可得） \]

\[V_甲<V_乙 \]

\[m_甲<m_乙 \]

\[S_甲<S_乙 \]

接下来，由于切下质量相等的一部分并各自叠放（换头），各自质量一定不变，即：

\[m'_甲=m'_乙 \]

可推出：

\[F_甲=F_乙 \]

A选项中\(S_甲\)变小，\(S_乙\)不变，故\(S'_甲<S'_乙\)，\(p_甲>p_乙\)，正确。
B选项中\(S_甲\)不变，\(S_乙\)变小，故\(p_乙\)变大，\(p_甲\)一定小于\(p_乙\)，错误。
C选项中\(S_甲\)、\(S_乙\)均不变，\(F\)也不变，因此\(p_甲=p_乙\)，错误。
D选项是最难的一个。均竖直切，那如何通过底面积反推到压强上去呢？其实，我们可以使用变化量比较法来解决。容易发现，甲、乙要切去底面积相等的一部分（原因是，由\(ρ_甲gh_甲=ρ_乙gh_乙\)可得\(ρ_甲h_甲=ρ_乙h_乙\)，此时希望切去质量相等的一部分即\(ρ_甲\Delta S_甲h_甲=ρ_乙\Delta S_乙h_乙\)，所以\(\Delta S_甲=\Delta S_乙\)）。由于\(S_甲<S_乙\)，因此变化量相同时，剩余部分\(S'_甲<S'_乙\)，即可得\(p_甲>p_乙\)，错误。

这可以说是切切切问题的极限了。主要策略是列式子！
另外，巧妙运用排除法。

切切切问题（图像版）

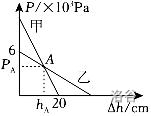
质量分布均匀的实心正方体甲、乙放在水平地面上，将甲、乙沿水平方向切去高度\(\Delta h\)，剩余部分对地面的压强\(p\)与\(\Delta h\)的关系如图所示。已知\(ρ_甲=6g/cm^3\)，乙的边长为\(30cm\)，下列选项正确的是：

A. 图中\(h_A\)的大小为\(15cm\)。
B. 乙的密度为\(3g/cm^3\)。
C. 未切前，甲物体的重力为\(240N\)。
D. 若将甲叠放在乙的正上方，甲对乙的压强为\(p_1\)；若将乙叠放在甲的正上方，乙对甲的压强为\(p_2\)，则\(p_1:p_2=2:1\)。

本题是切切切问题的衍生版：图像问题。解此类题目的策略也是按步分析。

首先，乙正好切完时\(\Delta h\)是\(30cm\)，没有问题。那接下来如何解呢？
既然\(A\)选项就让我们求\(h_A\)，即两条直线的交点……两条直线！那我把解析式算出来你不就炸了吗？

\[p_乙=-0.2\Delta h+6 \]

\[p_甲=... \]

首先计算一下甲的原压强。

\[p_0=ρ_甲gh_甲=6g/cm^3\cdot 10N/kg\cdot 20cm=12×10^3Pa \]

\[p_甲=-0.6\Delta h+12 \]

联立求解，得到：

\[\left\{\begin{aligned}&h_A=15\\&p_A=3\end{aligned}\right. \]

A选项，正确。

B选项可直接由乙的原压强反推：

\[ρ_乙=\frac {p_乙} {gh_乙}=\frac {6000Pa} {10N/kg\times 30cm}=2g/cm^3 \]

C选项可直接用\(F=pS\)得到：

\[G_甲=F=p_甲S_甲=12000Pa\times 400cm^2=480N \]

D选项对于选择题有一个巧算的方法，即：

\[\because S_甲<S_乙 \]

\[\therefore p_1=p_甲=12000Pa \]

说明：甲放在乙上和甲放在地面上没有区别。

\[\therefore p_2>p_乙=6000Pa \]

说明：甲的底面积比乙小，因此受力面积按甲的算。

\[\therefore p_1:p_2<2:1😎 \]

下面是正常方法的求解过程。

\[\because S_1=S_2=S_甲 \]

\[经过计算，G_甲:G_乙=8:9 \]

\[\therefore p_甲:p_乙=8:9\neq 2:1😉 \]

总结

固体压强问题其实算不上难，只能算复杂，在计算时要耐下性子来，对于定性分析，要列出等量关系和不等关系，逐一排除；对于定量计算，要理清条件和结论，并由条件和结论步步推理即可；对于有图像的一类题目，在处理时可以选择一些数学的方法。

补充：对于两个柱体，按照等质量、等体积、等厚度切法切出的\(p-m\)、\(p-V\)、\(p-h\)图像都是两条直线。等宽度切法切出的图像是平行于\(h\)轴的直线。

液体压强

三种容器的比较

余老师已经要求整理过，这里不再赘述。但是，需要看清题目中给出的条件，有时是质量相等，有时是液面相平。谨慎答题。

浮力（\(buoyance\)）

力学\(MVP\)的存在。

新考法：彩球温度计

请见校本。此类问题花样不多，校本上的题目已经可以覆盖。

定性分析

关于压强的定性分析也练过不少了，这里就不再赘述，按照平常的方法做即可。不过有一道题目比较新颖，在此呈现。

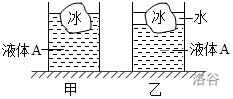
水平桌面上放有甲、乙两个完全相同的柱状容器。在甲容器内倒入\(A\)液体，乙容器内倒入部分\(A\)液体和水（液体和水不相溶，且\(ρ_A>ρ_水\)）。然后分别在两容器内放入质量相等的冰块，此时两容器内液面相平，如图所示。若冰块全部熔化后，甲、乙两容器内水面距离容器底部分别为\(h_1\)和\(h_2\)，水和液体\(A\)之间的界面距离容器底部分别为\(h'_1\)和\(h'_2\)，则：

A. \(h_1>h_2, h_1'>h_2'\)
B. \(h_1<h_2, h_1'>h_2'\)
C. \(h_1>h_2, h_1'<h_2'\)
D. \(h_1<h_2, h_1'<h_2'\)

我们需要说明的是，如果真正在考场上不会做了，可以使用如下的极限法：

假设冰块熔化前，水和液体\(A\)的界面在冰块之下：

对于甲容器，因为\(ρ_A>ρ_水\)，相当于在盐水中熔化一块冰，结合海平面上升，因此液面上升；
对于乙容器，上半部分相当于在水中熔化一块冰，因此液面不变。简要证明如下：

\[V_{排冰}=\frac {F_浮} {ρ_水g}=\frac {G_冰} {ρ_水g}=\frac {ρ_冰gV_冰} {ρ_水g} \]

\[将ρ_冰=0.9g/cm^3和ρ_水=1g/cm^3代入： \]

\[V_{排冰}=0.9V_冰 \]

\[又因为，冰熔化后，体积变为： \]

\[V'=\frac {m_冰} {ρ_水}=\frac {ρ_冰V_冰} {ρ_水}=0.9V_冰 \]

\[\therefore V'=V_{排冰}，恰好填满排开的空隙，液面不变。 \]

这样一来，乙容器液面不变，最终液面高度\(h_1>h_2\)。

对于\(h_1'\)和\(h_2'\)的话，可以使用下面的分析策略：

甲容器中，冰熔化，液体\(A\)的液面会下降，水漂在\(A\)上。但是，液体\(A\)液面再降也不会超过冰的最低点。（很明显嘛，冰排开的那一块左右不是还有液体，可以填充一些深度。）
乙容器中同样采用极限法，界面不会受到熔化的影响，因此不变。但是，乙容器中的界面始终比冰的最低点低。

问题显然转化成了比冰的最低点。

我们可以发现，冰的质量相同，因此浮力相同，因此排开液体的质量相同。对于甲容器，冰排开的是液体\(A\)；乙容器，冰排开的是水。因为\(ρ_A>ρ_水\)，所以\(V_{排甲}<V_{排乙}\)，甲容器冰的最低点比乙容器还高呢。

所以有如下关系：

\[h'_1>h_{甲容器内冰最低点}>h_{乙容器内冰最低点}>h_2' \]

\[\therefore h_1'>h_2' \]

极限法在考试中（尤其是特长生竞赛中）是非常好使的。常规方法的好处是严谨，但弊端也显然易见——太复杂、太耗时了。极限法用一种巧妙的方法，规避了这种严谨的关系推导和证明。

注意：极限法的要求是保证题目中条件没有明确规定你所取的特殊情况，并且题目结论对你的特殊情况通用。因此，极限法又被称为“特殊值法”。

练习

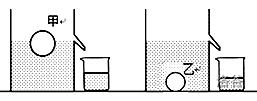
水平桌面上有两个完全相同的溢水杯和烧杯，溢水杯中装满水。将甲、乙两个实心小球分别放入溢水杯中，最终甲漂浮，乙沉底，如图所示。设甲烧杯中水的质量为\(m_甲\)，乙烧杯中水的质量为\(m_乙\)，现有以下判断：

\((1)\)若\(m_a>m_b\)，则一定有\(m_甲>m_乙\)。
\((2)\)若\(m_甲>m_乙\)，则一定有\(m_a>m_b\)。
\((3)\)若\(V_a>V_b\)，则一定有\(m_甲>m_乙\)。
\((4)\)若\(m_甲>m_乙\)，则一定有\(V_a>V_b\)。

其中正确的是（ \(C\) ）

A. \((1)(2)\)
B. \((3)(4)\)
C. \((1)(4)\)
D. \((2)(4)\)

定量计算

同样的，这里搞个典型的题目了解一下。

将密度为\(0.9g/cm^3\)，边长为\(10cm\)的立方体冰块，放入盛有水的柱形容器中，静止时冰块有\(2cm\)露出水面，如图所示。对容器缓慢加热， 直至冰块完全熔化。在冰熔化过程中，下列判断正确的是：（忽略水的蒸发和升华）

A. 未加热前，冰块处于漂浮状态。
B. 未加热前，冰块所受浮力为\(8N\)。
C. 加热后，冰的质量减小，冰的密度增大。
D. 加热后，冰块漂浮，受到的浮力保持不变。

\(A\)选项，一眼假，冰块没浮起来呢，怎么算漂浮呢。

注：这里有的同学要抬杠，说如果冰块对底部只接触不挤压呢，这不就漂了？

物体的漂浮推论是：

\[\frac {V_排} {V_物}=\frac {ρ_物}{ρ_液} \]

证明十分好证，你给它交叉相乘，两边同时乘个\(g\)，不就是\(G_物=F_浮\)吗？
因此，对于本题，\(\frac {V_排} {V_物}=\frac {0.9}{1}=\frac 9 {10}\)，也就是说，冰块体积的十分之九要浸入水内。那你看，这题是不是只浸没了十分之八？所以不是漂浮。

漂浮推论很好用！很好用！一定要记住。

\(B\)选项，算一下。

\[F_浮=ρ_液gV_排=1g/cm^3\times 10N/kg\times 10cm\times 10cm\times (10cm-2cm)=8N \]

顺便说一嘴，考试不能像我这样写，容易扣分。

\(C\)选项，冰的密度怎么可能变大呢，一眼假。

\(D\)选项，冰块变小了，自重都变小了，浮力怎么可能不变呢。

特殊方法测密度

小红在厨房里帮妈妈洗菜，发现茄子放在水中，有一半左右露出水面。小红想利用柱形水桶和刻度尺测量茄子的密度，但是她发现，实验数据比较小，很难测量。于是她做了如下改进方案，方案可行的是：

A. 增加桶内水的深度；
B. 减小桶内水的质量；
C. 向水中加盐增大水的密度；
D. 减小柱形水桶的底面积。

本题新颖的地方在于，我们需要解决三个问题：

1. 密度怎么测的？
2. 什么实验数据？
3. 为什么会偏小？

第一个问题，相信题目做得多的同学一眼就能看出来。
柱形容器加刻度尺？不就是先漂浮，再浸没，测水位高度嘛。

第二个问题就显而易见了，肯定是高度……吗？
其实是我们拿来运算的高度差（\(\Delta H\)）。

第三个问题，浸没后明明排开液体体积一样，但为什么上升的高度差很小呢？很简单，就是容器太宽了。

搞窄一点就行了，因此选\(D\)。这种题目新在没有告诉你测密度的方法，需要推导它是怎么测的。切忌读完题目一脸懵，直接瞎选一个。耐心理清思路，你可能会有不一样的结果。