题解：CF1491G Switch and Flip

posted on 2024-12-26 05:29:56 | under | source

挺妙的一题，不过慢慢推还是能推出来的。

考虑 \(c_i\to i\) 连边，则得到若干个环。一次操作 \((x,y)\) 会交换 \(x,y\) 两个点的出边，且将 \(x,y\) 取反，目标是全变成自环且均为正。

自然会想到考察交换一条环边两端节点带来的影响，因为只有这样才能得到子环，对 \(a\to b\) 交换如下图：

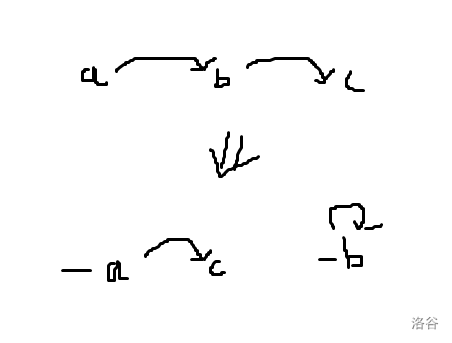
相当于将 \(b\) 从环上剥出来。然后考虑对一个环进行操作，为了尽量抵消取反，那么我肯定优先让被取反过的点作为 \(a\to b\) 中的 \(b\)，这样就可以得到一个未被取反的自环。但不幸的是，按上述方式操作一定会有两个点被取反。

但是你惊喜的发现，可以对两个环上的点进行交换，这样会合并为一个大环，且大环恰有两个取反的点：

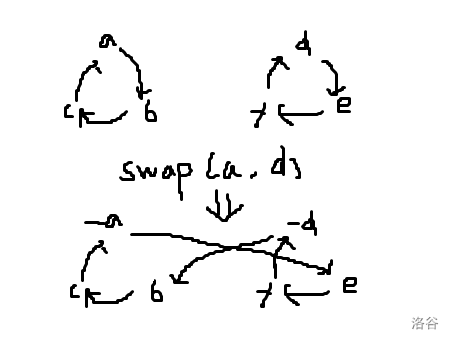
现在考虑恰好取反这两个点：当环大小 \(\ge 3\) 时，必然有一个取反点满足其前驱未被取反，那么交换它们两，就可以剥出一个未取反的自环，同时前驱被取反，递归下去。最终大小 \(=2\) 时直接交换即可。

于是，可以选取两个环 \(A,B\)，通过 \(|A|+|B|\) 步将两个环分解为自环。

假如环数是奇数，则会剩下一个环。可以将其与先前一个自环进行操作。假如一开始只有一个环怎么办？大力构造！

若其大小 \(=3\)，可以通过两步使两个点被取反然后解决：

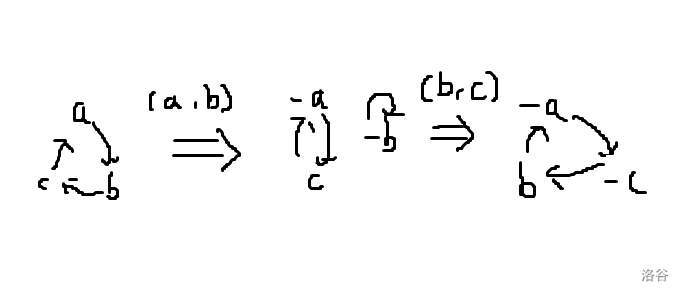
若其大小 \(>3\)，可以选取两个不相邻的点交换，分割为两个恰有一个取反点的环。一直进行操作，直到两环大小分别为 \(1,2\)，发现就是上图中间的情况，可以 \(3\) 步解决。总次数为 \(n+1\)。

代码

写死我了。实现略丑，慎看。

#include<bits/stdc++.h>
using namespace std;

const int N = 3e5 + 5;
int n, fa[N], nxt[N], pre[N], cir;
bool col[N];
vector<int> buc[N], Cir;
vector<pair<int, int> > ans;

inline void debug(){
	for(int i = 1; i <= n; ++i) cout << nxt[i] << ' ';
	cout << endl;
}
inline int find(int u) {return fa[u] == u ? u : fa[u] = find(fa[u]);}
inline void initcir(){
	for(int i = 1; i <= n; ++i) fa[i] = i, buc[i].clear();
	for(int i = 1; i <= n; ++i) fa[find(i)] = find(nxt[i]);
	Cir.clear();
	for(int i = 1; i <= n; ++i){
		buc[find(i)].push_back(i);
		if(fa[i] == i) Cir.push_back(i);
	}
	/*
	for(auto i : Cir){
		for(auto j : buc[i])
			cout << j << ' ';
		cout << endl;
	}
	*/
}
inline void swp(int x, int y){
	ans.push_back({nxt[x], nxt[y]});
	col[x] ^= 1, col[y] ^= 1;
	swap(pre[nxt[x]], pre[nxt[y]]);
	swap(nxt[x], nxt[y]);
}
inline void solve(int id){
//	debug();
	int x = -1, y = -1, m = buc[id].size();
	for(auto i : buc[id])
		if(col[i]){
			if(x == -1) x = i;
			else y = i;
		}
//	cout << x << ' ' << y << ' ' << m << endl;
	while(m > 2){
		if(pre[x] == y) swap(x, y);
		int _x = pre[x];
		swp(_x, x);
		x = _x;
		--m;
	}
	swp(x, y);
}
inline void solve2(int fir, int sec){
	int x = buc[fir].back(), y = buc[sec].back();
	swp(x, y);
	int fx = find(x), fy = find(y); 
	for(auto i : buc[fx]) buc[fy].push_back(i);
	fa[fx] = fy;
	solve(fy);
}
inline int solve3(int id, int lim){
	int x, m = buc[id].size();
	for(auto i : buc[id]) if(col[i]) x = i;
	while(m > lim){
		int _x = pre[x];
		swp(_x, x);
		x = _x;
		--m;
	}
	return x;
}
inline void calc1(){
	if(n == 3) swp(1, nxt[1]), swp(nxt[1], 5 - nxt[1]), solve(find(1));
	else{
		int p;
		for(int i = 2; i <= n; ++i) if(pre[1] != i && nxt[1] != i) p = i;
		swp(1, p), initcir();
		int fir = Cir[0], sec = Cir[1];
		if(buc[sec].size() == 1) swap(fir, sec);
		int a = solve3(fir, 1), b = solve3(sec, 2), c = pre[b];
		swp(a, c), swp(a, b), swp(a, c);
	}
}
inline void calc2(){
	while(Cir.size() >= 2){
		int fir = Cir.back(); Cir.pop_back();
		int sec = Cir.back(); Cir.pop_back();
		solve2(fir, sec);
	}
	if(!Cir.empty()){
		int fir = Cir.back(), sec;
		for(int i = 1; i <= n; ++i) if(find(i) != fir) sec = i;
		swp(buc[fir][0], sec), buc[fir].push_back(sec);
		solve(fir);
	}
}
signed main(){
	cin >> n;
	for(int i = 1; i <= n; ++i) scanf("%d", &pre[i]), nxt[pre[i]] = i;
	initcir();
	if(Cir.size() == 1) calc1();
	else calc2();
	printf("%d\n", ans.size());
	for(auto [x, y] : ans) printf("%d %d\n", x, y);
	return 0;
}