题解：AT_agc015_d [AGC015D] A or---or B Problem

posted on 2024-11-14 00:57:53 | under | source

闲话：考场做法，比较奇怪。

为了方便起见，令 \(l\gets l-1,r\gets r+1\)，求 \((l,r)\) 的答案。

套路的，考虑将区间内的数划分区间。

从高位向低位看，首先去掉 \(l,r\) 的相同前缀，然后将数分为第一位为 \(0\) 和第一位为 \(1\) 的，记为 \(0\) 类数和 \(1\) 类数。

对于 \(0\) 类数可以分为 \(\log\) 个区间，具体而言，其实就是最高位到第 \(i\) 位与 \(l\) 一样，然后第 \(i-1\) 位是 \(1\)（\(l\) 第 \(i-1\) 位是 \(0\)），这样 \([0,i-2]\) 位就能随便取。

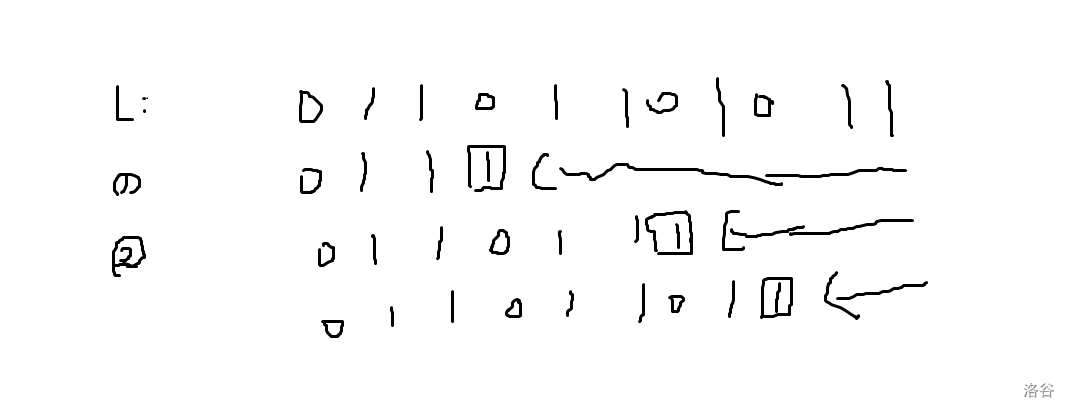
划分如上图，注意到假如选取了集合 \(i\)，那么没有必要选集合 \(i<j\) 了，因为没影响。记下 \(a_i\) 表示第 \(i\) 个集合在 \([0,i)\) 位可以随便取。那么只选 \(l\) 集合的数，也就是令最高位为 \(0\) 的方案为 \(\sum 2^{a_i}\)。

对于 \(1\) 类数也同理，划分如下：

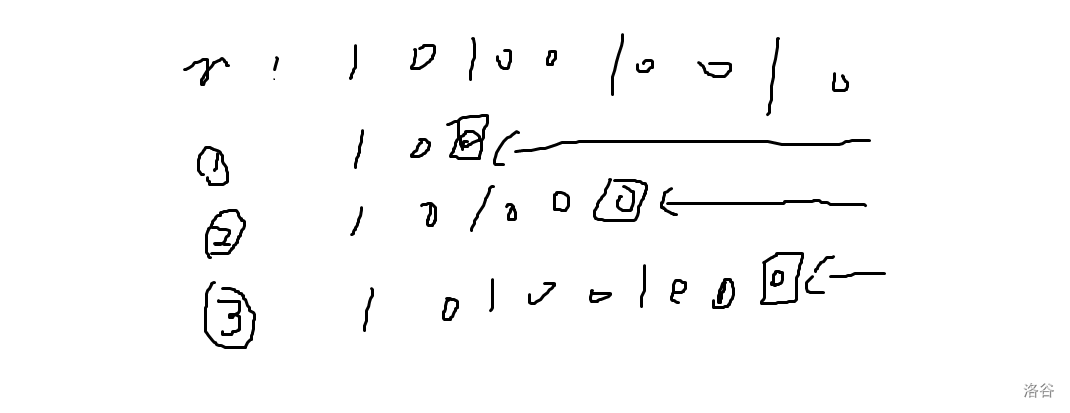
记集合 \(1\) 在 \([0,i)\) 位可以随便取，那么只用它可以凑出所有数 \(x\)，\(x\) 满足其最高位为 \(1\)，然后一直到 \(i\) 位都是 \(0\)，第 \([0,i)\) 位随意。注意到其它集合的唯一作用是与集合 \(1\) 搭配，使得 \(x\) 的第 \(i\) 位也可以为 \(1\)。

综上，\(1\) 类数可以凑出的数形如：最高位为 \(1\) 然后跟着若干个连续 \(0\)，之后 \([0,k)\) 位随便取。总数为 \(2^k\)。

现在考虑同时选了 \(0\) 类数和 \(1\) 类数。实际上就是在 \(0\) 类数的基础上，令最高位为 \(1\)，然后允许第 \([0,k)\) 位可以放 \(1\)：

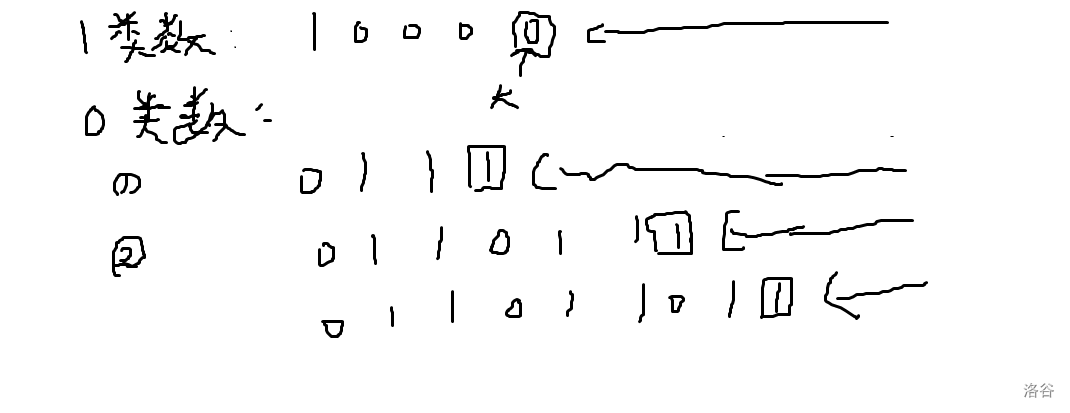
首先假如 \(1\) 类数除了最高位都是 \(0\)，那么就有 \(\sum 2^{a_i}\) 种方案。可以发现，假如 \(1\) 类数除了最高位还存在一个 \(1\)，那么一定会算重，所以不用考虑。

结束了吗？没有，刚刚还是会算重，具体来说，假如选取的 \(0\) 类数集合最高位到第 \(p\) 位都是 \(0\)，那么在 \(p\le k\) 时就会和“只选 \(1\) 类数”的方案重复。这也很好理解，因为它不会改变最高位到第 \(k\) 位的状态。也就是说我们只在 \(p>k\) 时统计即可。

复杂度 \(O(\log V)\)。

代码

#include<bits/stdc++.h>
using namespace std;

#define int long long
const int N = 62;
int T, a, b, ans, pw[N], c;
vector<pair<int, int> > A;
vector<int> B;

inline int get(int x, int p) {return (x >> p) & 1;}
inline int dif(int a, int b){
	for(int i = 60; i; --i)
		if(get(a, i) ^ get(b, i)) return i;
}
signed main(){
	pw[0] = 1;
	for(int i = 1; i < N; ++i) pw[i] = pw[i - 1] * 2ll;
	
	scanf("%lld%lld", &a, &b), --a, ++b;
	ans = 0, A.clear(), B.clear();
	int pos = dif(a, b); //第一个不同的位
	for(int i = pos - 1, pd = -1; ~i; --i){
		if(!get(a, i)) A.push_back({i, max(pd, i)}); //0类数集合，二元组(x,y)表示[0,x)位随便取，最高位的1在第y位
		if(get(b, i)) B.push_back(i); //1类数集合
		if(pd == -1 && get(a, i)) pd = i;
	}
	for(auto i : A) ans += pw[i.first]; //计算只选0类数
	if(B.empty()) printf("%lld\n", ans); //假如不存在1类数
	else{
		c = B[0] + (B.size() > 1); //计算只选1类数
		ans += pw[c];
		for(auto i : A)	if(i.second >= c) ans += pw[i.first]; //计算同时选0,1类数
		printf("%lld\n", ans);
	}
	return 0;
}