联合省选2024 D2T1

posted on 2024-03-22 05:28:31 | under | source

神仙题，完美诠释算法全都会但就是不会做的现象。

直接贪心之类的？不可行，没有一点头绪。那么考虑弱一点的问题，只要求出答案的第一位。这就是突破口。显然有个归并排序加 \(\rm dp\) 的做法，也可以二分，复杂度多个 \(\log\)。

继续推，发现确定了第一位 \(p\)，则根节点到 \(p\) 的路径唯一，将原树分成了若干个满二叉树，并会按照深搜回溯逐次遍历它们。图示如下：（考场止步于此 qwq）

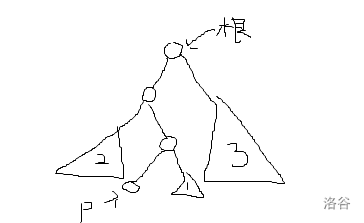
然后发现划分出来的子树，它们几乎是互相独立的，即可以分治地处理它们内部的字典序。唯一的限制，是必须保证 \(p\) 为答案的第一位。

令 \(f_i\) 表示 \(i\) 子树中满足 \(<p\) 的符文都无法被取为第一位的最小花费。那么单独拎出一棵根为 \(s\) 的子树，只要满足其初始携带的魔力值 \(\ge f_s\)，就能保证其答案字典序的第一位 \(\ge p\)。

这是因为每次都选择最大的作为第一位，那么只要携带的魔力值足够，就能使得第一位 \(\ge q\)。这一点不是很好想。

也就是说，只要为每个子树 \(s\) 留下 \(\ge f_s\) 的魔力值，就能使得 \(p\) 是最终答案的第一位。

我们是逐层遍历这些子树的，并且一定要遍历完才能跳到下一个子树。所以最终答案呈 \(p,{ans_1},{ans_2}...\) 的形式。贪心地，我们希望留给排在后面子树的魔力值尽量小。

这个过程可以 \(\rm dfs\) 实现。令函数 \(dfs(u,k)\) 表示携带 \(k\) 魔力值进入 \(u\) 子树，并返回花费多少魔力值。

首先找到它的第一位 \(p\)，分类讨论：

• 若 \(p\) 在右子树：

先让 \(res=dfs(rson,k-f_{lson})\)，表示为 \(lson\) 留下足够的魔力值。然后遍历 \(dfs(lson,k-res)\)，返回值就是两次 \(dfs\) 的和。

• 若 \(p\) 在左子树：

同上，但是可以激活 \(u\) 的守卫。令 \(res=dfs(lson,k-\min(f_{rson},a_u))\)。

接下来注意不是 \(a_u\le f_{rson}\) 就选择激活守卫，因为激活它只是保证了当前层最优，却让 \(rson\) 可携带的魔力值白白少了 \(a_u\)。那么只有当剩下的魔力值不足以支付 \(f_{rson}\)（\(k-res<f_{rson}\)）时必须选 \(a_u\)。最后计算花费即可。

复杂度 \(O(n^22^n)\)，可以归并优化至 \(O(n2^n)\)。

代码

不是归并写不起，而是二分更有性价比。 二分做法最慢一个点只跑了 88ms 你敢信。

#include<bits/stdc++.h>
using namespace std;

#define int long long
const int N = 3e5 + 5, inf = 1e18;
int T, n, K, a[N], q[N], f[N], ans[N], Ans, from, id[N];

inline void check(int u, int p){
	if(u >= 1 << n) {f[u] = (q[u] < p ? inf : 0); return ;}
	check(u << 1, p), check(u << 1 | 1, p);
	f[u] = min(f[u << 1] + min(f[u << 1 | 1], a[u]), inf);
}
inline void get_first(int u, int k){
	int l = 1, r = (1 << n) + 1, mid;
	while(l + 1 < r){
		mid = l + r >> 1, check(u, mid);
		if(f[u] <= k) l = mid;
		else r = mid;
	}
	check(u, l); 
	int L = id[l]; while((L >> 1) > u) L >>= 1; from = L & 1;
}
inline int dfs(int u, int k){
	if(u >= 1 << n) {ans[++Ans] = q[u]; return 0;}
	get_first(u, k);
	if(!from){ //左子树
		int klt = dfs(u << 1, k - min(f[u << 1 | 1], a[u]));
		if(k - klt < f[u << 1 | 1]) return klt + a[u] + dfs(u << 1 | 1, k - klt - a[u]);
		return klt + dfs(u << 1 | 1, k - klt);
	}
	else{
		int krt = dfs(u << 1 | 1, k - f[u << 1]);
		return krt + dfs(u << 1, k - krt);
	} 
}
signed main(){
	cin >> T;
	while(T--){
		scanf("%lld%lld", &n, &K), Ans = 0;
		for(int i = 1; i < 1 << n; ++i) scanf("%lld", &a[i]);
		for(int i = 1 << n; i < 1 << n + 1; ++i) scanf("%lld", &q[i]), id[q[i]] = i;
		dfs(1, K);
		for(int i = 1; i <= 1 << n; ++i) printf("%lld ", ans[i]);
		putchar('\n');
	}
	return 0;
}