WC2025 思维题选讲

posted on 2025-02-07 07:12:49 | under | source

[AGC068E] Sort and Match

题意：给定矩阵 \(a_{i,j}\)，将序列 \(x\) 升序排序得到 \(y\)，则 \(val(x)=\prod a_{x_i,y_i}\)。求所有 \(x_i\in [1,n]\) 的序列的权值之和。\(n\le 50\)。

神似积和式，难以处理。注意到 \(a\) 形如邻接矩阵，将 \(x,y\) 映射到有向图上。令 \(y_i\to x_i\) 连边即可。为了构成双射，认为一个点的出边有顺序。

注意到图为欧拉图。考虑以游走的形式刻画有向图：分别从 \(st=1\dots n\) 为起点开始游走，每次允许走向任意 \(\ge st\) 的点，最后回到 \(st\)。在游走过程中，可能会产生其它的环（甚至是自环），会算重吗？并不会，因为认为出边有顺序。恰好与有向图构成双射，十分巧妙。

游走过程是容易 dp 的，设计 \(f_{i,j,k}\) 为起点为 \(i\)、走到了 \(j\)、走了 \(k\) 条边时的权值之和。本题对不同起点统计答案，只需倒着做即可。\(O(n^4)\)。

代码灰常好写，就注意一下转移时的循环顺序？

[AGC055F] Creative Splitting

题意：对于一个 \(nm\) 的序列 \(a\)，若可以将其剖分为 \(n\) 个长 \(m\) 的子序列，满足每个子序列第 \(i\) 项 \(\le i\)，则称它是合法的。分别假设 \(a_x=y\)，求合法的 \(a\) 的数量。\(n,m\le 20\)。

做法源自 WC2025 郭羽冲大蛇的讲解，和现有题解貌似不太一样？

典中典之寻找充要条件，从后往前贪心填写子序列，记 \(b_i\) 表示第 \(i\) 个子序列接下来填的位置，对于 \(a_i\) 找到可以容下它的最小的 \(b_j\)。容易反证法证明。

令 \(b\) 升序排列，特殊地 \(b_{n+1}=m\)。考虑通过 \(b\) 的变化反推 \(a\)，具体来说，填写 \(a_i\) 时，选取一个 \(b_j\) 填进去，则 \(a_i\) 有 \(b_{j+1}-b_j\) 种取值方案。

记 \(c=b_{i}-b_{i-1}\)，那么等价于选取 \(j\) 然后产生 \(c_j\) 的贡献，并让 \(c_j-1\)，\(c_{j+1}+1\)。

注意到 \(-1+1\) 的过程可以用小球的移动来刻画，同时不同小球的选取又能体现 \(\times c\)。于是不考虑限制的情况下，一个合法 \(a\) 序列等价于下列过程：有 \(m\) 个小球，一开始位于 \(1\)，每次可以选取一个向右移动一格，最后全移到 \(n+1\)。\(c_i\) 就是位置 \(i\) 上的小球数量。

考虑 \(a_x=y\) 带来的限制。不妨分为两个阶段：第一阶段即前 \(nm-x\) 步、第二阶段即后 \(x\) 步。枚举 \(a_x\) 填到了 \(b_t\)，那么要求第一阶段结束后 \(\sum\limits_{i<t} c_i<y\le \sum\limits_{i\le t} c_i\)。可以差分拆一下，只考虑右边这个限制即可。\(\sum\limits_{i\le t}c_i\) 又等价于前 \(t\) 个位置上的球数。

考虑通过球的移动刻画第 \(nm-x+1\) 步（即 \(a_x=y\)），你找到 \(y\) 对应的那个球在移动显然不现实，不妨移动编号最小的球，这样十分方便计数。

终于可以 dp 了！记 \(lim\) 为我们关心的前 \(lim\) 个位置（需要满足这些位置上的球数 \(\ge y\)）。记 \(f_{i,j,k,st}\) 为考虑前 \(i\) 个球、第一阶段有 \(j\) 个操作、在第一阶段移动到的位置 \(\le lim\) 的球数量为 \(k\)。\(st\) 用于处理第 \(nm-x+1\) 步，\(st=0\) 表示此前不存在在第一阶段移动了 \(t-1\) 步的球，即已经有小球被安排在 \(nm-x+1\) 步移动了，\(st=1\) 反之。

转移灰常容易，枚举当前球在第一阶段操作数即可。最后算答案就 \(ans_{x,y}\gets fl\times \sum\limits_{k\ge y}f_{m,nm-x,k,1}\)。\(fl\) 是差分标记。

复杂度 \(O(n^3m^3)\)。

CF1806F2 GCD Master (hard version)

题意：给序列 \(|a|=n\)，进行恰好 \(k\) 次合并，权值为每个集合 \(\gcd\) 之和，最大化权值。\(k<n\le 1e6,a\le 1e18\)。

首先，等价于划分为 \(n-k\) 个集合。

• 引理：令 \(a<b\)，则 \(gcd(a,b)\le \frac b2\)。

于是，若存在两个集合 \(S,T\) 满足 \(S,T\) 均有至少两种元素，那么将 \(S,T\) 最大的那个拎出来做一个集合，那么显然是比原先的优。

• 性质 1：最优解至多存在一个集合满足有不同元素。

调整法易证。

不妨将操作视为合并相同元素、合并不同元素两种。枚举第二种操作次数 \(t\)。先进行第一种，相当于消掉一个元素（前提是至少有两个该种元素），那么找前 \(k-t\) 小即可。

那么考虑第二种操作，抽出不相同的元素构成 \(b\)，求一个 \(|B|=t\)，最大化 \(\gcd(B_1\dots B_t)-\sum B\)。

注意到若存在 \(u<v<w\)，满足 \(v,w\in B,u\notin B\)，那么改 \(w\) 选择 \(u\) 更优。修改后记为 \(B^\prime\)。证明如下：

\(val(B^\prime)\ge \sum B^\prime=\sum B+w-u\ge \sum B+\gcd(w-v)\ge val(B)\)

• 性质 2：最优解形如一个前缀加一个孤立点。

调整法易证。

直接枚举就是 \(O(n^2\log V)\) 的。但你注意到若 \(\gcd(b_1\dots b_t)=\gcd(b_1\dots b_{t+1})\) 那么直接选 \(b_{t+1}\) 最优。而不满足这个条件的位置 \(O(\log V)\) 个，就能 \(O(n\log^2 V)\) 了。

瓶颈在于对同一个 \(b_j\) 计算多次形如 \(\gcd(b_j,gcd(b_1\dots b_t))\)，不妨记下上一次 \(t^\prime\) 计算的结果 \(ans_j\)，答案就是 \(\gcd(ans_j,gcd(b_1\dots b_t))\)。显然 \(ans_i\) 的总计算量 \(O(\log V)\)，然后就单 \(\log\) 了。

P6545 [CEOI 2014] The Wall

题意：给一张网格，边有边权，给定关键格子，求一条最小权回路，满足包含左上角和所有关键格子。\(n,m\le 400\)。

感觉上是建图跑个最小环之类的东东，但是不好刻画“包含格子”这一限制。

需要注意到一个非常重要的结论：最优解一定包含左上角到关键格子左上角的最短路（任意一条）。

证明倒是容易，调整法即可，考虑最短路未被包含的部分，显然可以调整为包含它，这样代价更小格子却更多。

然后你发现只要回路不经过最短路就是合法的，这是容易刻画的。

具体来说：将一个格子拆成上下左右四个点并顺时针连边（权值为对应原边权），相邻且不同格子连 \(0\) 权边。相当于让回路稍稍飘离（抽象）。值得注意的是，边界也要建边不然最短路包括边界就炸了。白嫖一张图：

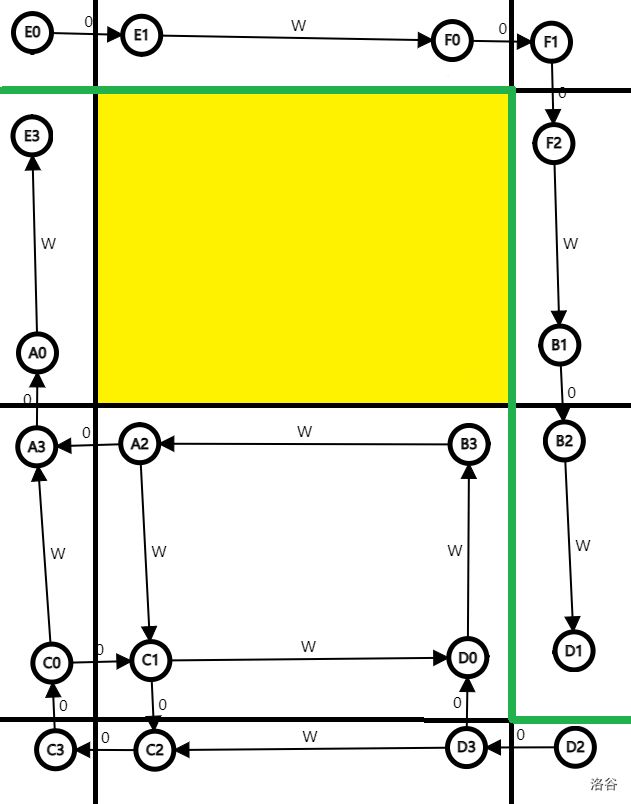
然后断一条左上角的边跑最短路即可。